习题4

习题4

1. 设向量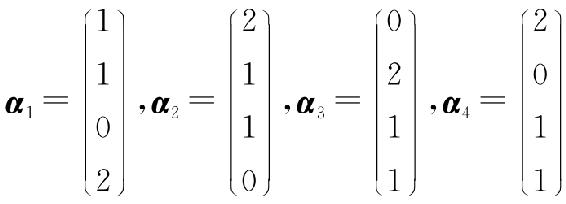，求2α1+α2+3α3-4α4.

2. 已知向量，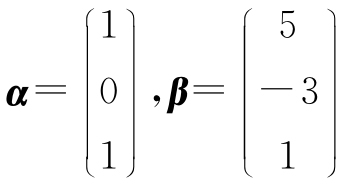

（1）设（α-ξ）+2（β-ξ）=3（α-β），求向量ξ；

（2）设2ξ-η=α，ξ+n=β，求向量ξ，η.

3. 设向量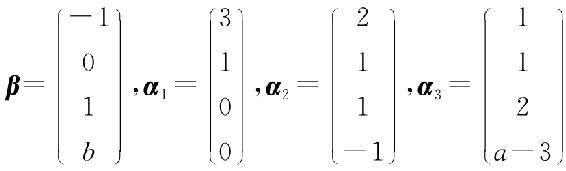，问a，b取何值时，β可由α1，α2，α3线性表示？并求此表达式.

4. 已知向量组

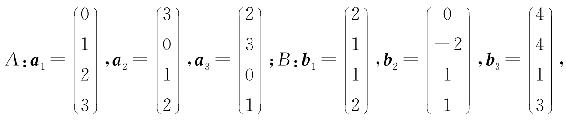
证明向量组B能由A线性表示，但向量组A不能由B线性表示.

5. 已知向量组

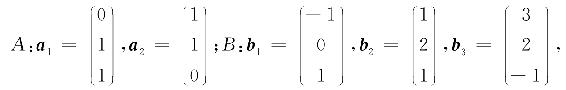
证明向量组A与B等价.

6. 判定下列向量组的线性相关性：

7. 举例说明下列各命题是错误的：

（1）若向量组a1，a2，…，am是线性相关的，则a1可由a2，…，am线性表示.

（2）若有不全为0的数λ1，λ2，…，λm，使

λ1a1+…+λmam+λ1b1+…+λmbm＝0

成立，则a1，a2，…，am线性相关，b1，b2，…，bm亦线性相关.

（3）若只有λ1，λ2…，λm全为0时，等式

λ1a1+…+λmam+λ1b1+…+λmbm=0

才能成立，则a1，a2，…，am线性无关，b1，b2，…，bm亦线性无关.

（4）若a1，…，am线性相关，b1，…，bm亦线性相关，则有不全为0的数λ1.…，λm，使

λla1+…+λmam＝0，A1b1+…+λmbm=0

同时成立.

8. 如果向量组a1，a2，…，am线性无关，试证明a1，a1+a2，….a1+a2+…+am也线性无关.

9. 如果向量组a1，a2，…，am线性无关，且

b1=a1+a2，b2=a2+a3，…，bm=am+a1，

试证明：（1）m为奇数时，b1，b2，…，bm线性无关；

（2）m为偶数时，b1，b2，…，bm线性相关.

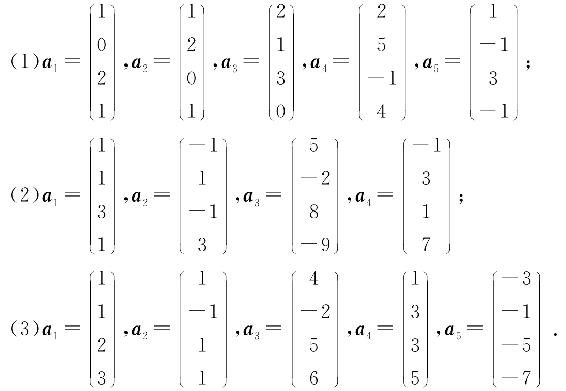
10. 求下列向量组的秩和一个最大无关组，并将剩余向量用最大无关组线性表示：

11. 设向量组

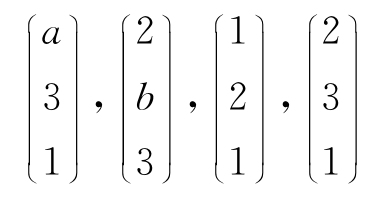
的秩为2，求a，b.

12. 设a1，a2，…，an是一组n维向量，已知n维单位坐标向量。e1，e2，…，en能由它们线性表示，证明a1，a2，…，an线性无关.

13. 设a1，a2，…，an是一组n维向量，证明它们线性无关的充分必要条件是：任一n维向量都可由它们线性表示.

14. 设向量组a1，a2，…，am线性相关，且a1≠0，证明存在某个向量ak（2≤k≤m），使ak能由a1，…，ak-1线性表示.

15. 设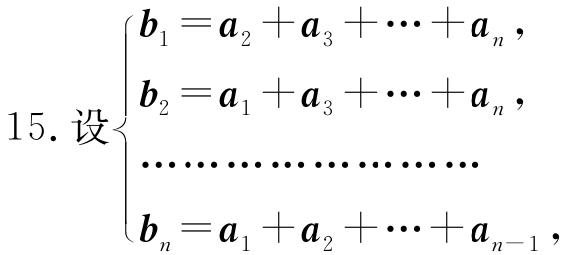

证明向量组a1，a2，…，an与向量组b1，b2，…，bn等价.

16. 已知3阶矩阵A与3维列向量x满足A3x=3Ax-A2x，且向量组x，Ax，A2x线性无关，

（1）记P=（x，Ax，A2x），求3阶矩阵B，使AP=PB;（2）求|A|.

17. 求解下列齐次线性方程组的基础解系：

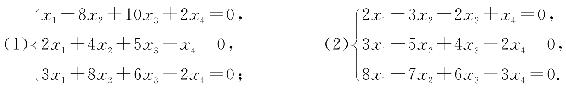
18. 设四元齐次线性方程组

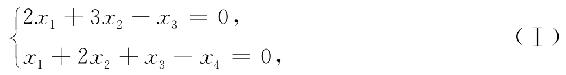
已知另一个四元齐次线性方程组（Ⅱ）的基础解系为

η1=（2，-1，a+2，1）T，η2=（-1，2，4.a+8）T

（1）求方程组（Ⅰ）的一个基础解系；

（2）当a为何值时，方程组（Ⅰ）与方程组（Ⅱ）有非零公共解？

19. 设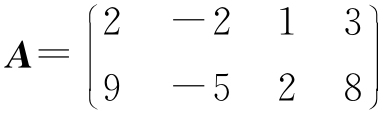，求一个4×2矩阵B，使AB=O，且R（B）=2.

20. 求一个齐次线性方程组，使它的基础解系为

ξ1=（0，1，2，3）T，ξ2，=（3，2，1，0）T.

21. 设n阶矩阵A满足A2=A，E为n阶单位矩阵，证明

R（A）+R（A-E）=n.

22. 设A为n阶矩阵（n≥2），A*为A的伴随矩阵，证明

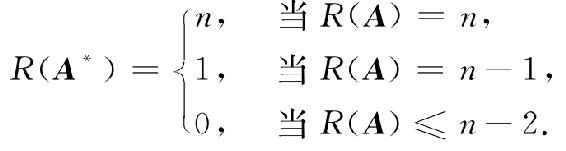
23. 求下列非齐次线性方程组的通解：

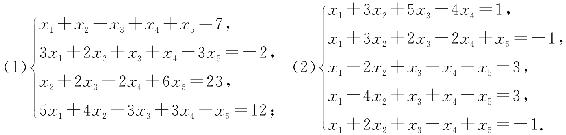
24. 设α1=（1，2，0）T，α2=（1，a+2，一3a）T，α3=（-1，-b-2，a+2b）T，β=（1，3，-3）T，试讨论当a，b为何值时：

（1）β不能由α1，α2，α3线性表示：

（2）β可由α1，α2，α3唯一地线性表示，并求出表示式；

（3）β可由α1，α2，α3线性表示，但表示不唯一，并求出表示式.

25. 设矩阵A=（a1，a2，a3，a4），其中，a2，a3，a4线性无关.a1=2a2-a3.向量 b=a1+a2+a3+a4，求方程组Ax=b的通解.

26. 设η*是非齐次线性方程组Ax=b的一个解，ξ1，…，ξn-r是对应的齐次线性方程组的一个基础解系，证明：

（1）η*，ξ1，…，ξn-r线性无关；

（2）η*，η*+ξ1，…，η*+ξn-r线性无关.

27. 设η1，…ηs是非齐次线性方程组Ax=b的s个解，k1，…，ks为实数，满足k1+k2…+ks=1，证明

x=k1η1+k2η2+…+ksηs

也是它的解.

28. 设非齐次线性方程组Ax=b的系数矩阵的秩为r，η1，…，ηn-r+1是它的n-r+1个线性无关的解（由26题知，它确有n-r+l个线性无关的解）. 试证明它的任一解可表示为

x=k1η1+k2η2+…+kn-r+1ηn-r+1（其中k1+k2+…+kn-r+1=1）.

29. 由a1=（1，1，0，0）T，a2=（1，0，1，1）T所生成的向量空间记为L1，由 b1=（2，-1，3，3）T，b2=（0，1，-1，-1）T所生成的向量空间记为L2，试证明L1=L2.

30. 验证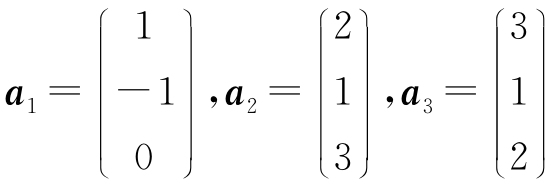为R3的一个基，并把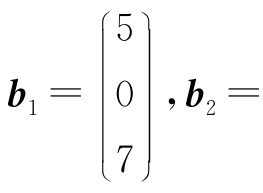，b2=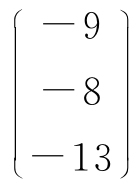用这个基线性表示.