5.1 向量的内积及正交性
5.1 向量的内积及正交性
5.1.1 向量的内积
定义1 设有n维向量
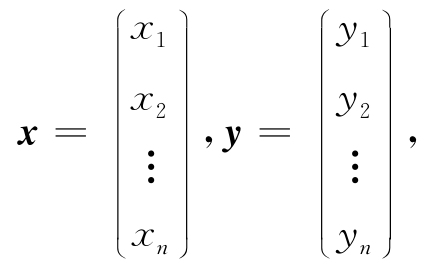
称xlyl+x2y2+…+xnyn为向量x与y的内积，记作[x，y]，即
[x，y]=xlyl+x2y2+…+xnyn.
内积是两个向量之间的一种运算，其结果是一个实数，将向量看成列矩阵，由矩阵乘法内积还可表示为
[x，y]＝xTy，
内积的运算规律（其中x，y，z为n维向量，λ为实数）：
（i）[x，y]=[y，x]；
（ii）[λx，y]=λ[x，y]；
（iii）[x+y，z]=[x，z]+[y，z]；
（iv）[x，x]≥0，当且仅当x=0时，[x，x]=0；
（v）柯西一施瓦茨（Cauchy-Schwarz）不等式：[x，y]2≤[x，x][y，y]，当且仅当x与y线性相关时等号成立.
5.1.2 向量的长度
定义2 设x是n维向量，称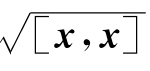
为向量x的长度（或范数），记作‖x‖. 即若x＝（x1，x2，…，xn）T，则有
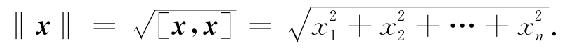
向量的长度具有以下性质：
（i）非负性 ‖x‖≥0，当且仅当x=0时等号成立；
（ii）齐次性 ‖λx‖=|λ|‖x‖，λ为任意实数；
（iii）三角不等式 ‖x+y‖≤‖x‖+‖y‖.
证 （i）与（ii）是显然的，下面证明（iii）.
‖x+y‖2=[x+y，x+y]=[x，x]+2[x，y]+[y，y]，
由柯西一施瓦茨不等式，有
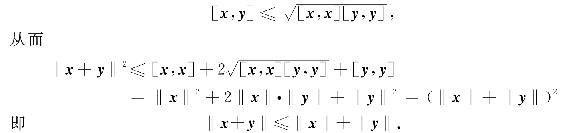
若‖x‖=1，则称x为单位向量.
设a为任意非零向量，则向量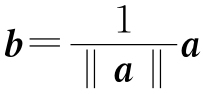
为单位向量，因为
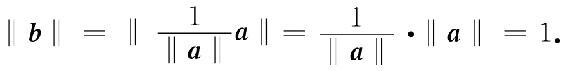
对于一个非零向量，用a的长度‖a‖去除a，即得到一个单位向量，这个过程称为将a单位化.
5.1.3 向量的夹角与正交向量组
由柯西一施瓦茨不等式，有
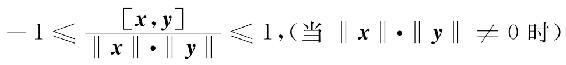
于是对Rn中的向量引入夹角的概念.
定义3 设向量x与y均是n维非零向量，称
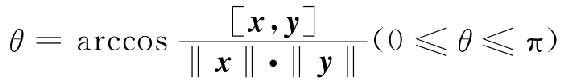
为向量x与y的夹角.
当[x，y]=0时，称向量x与y正交. 显然，零向量与任何向量都正交.
两两正交的非零向量组，称为正交向量组.
定理1 若向量组a1，a2，…，am是正交向量组，则a1，a2，…，am线性无关.
证 设有k1，k2，…，km使
k1a1+k2a2+…+kmam=0，
用ai（i=1，2，…，m）与上式两端作内积，得
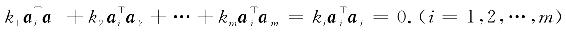
因为ai≠0，所以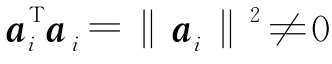
，从而必有
ki=0，（i=1，2，…，m）
故向量组a1，a2，…，am线性无关.
例5.1 已知三维向量空间R3中两个向量正交，
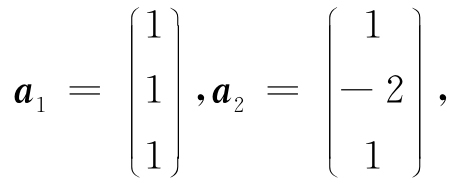
试求一个非零向量a3，使a1，a2，a3两两正交.
解 记
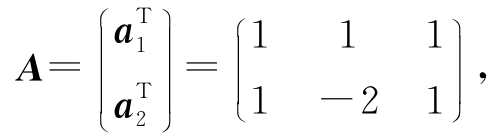
a3应满足齐次线性方程组Ax=0，即
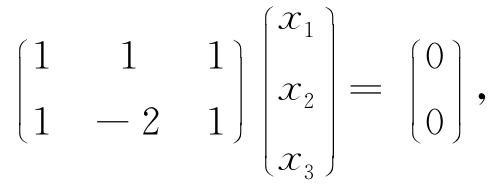
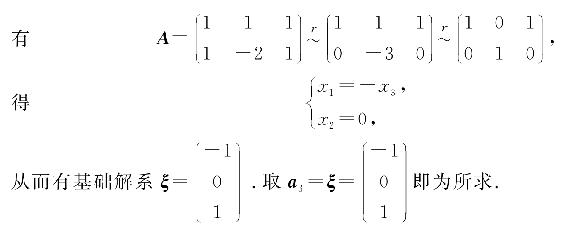
定义4 设n维向量组e1，e2，…，er是向量空间
的一个基，若e1，e2，…，er两两正交，且都是单位向量，则称el，e2，…，er是V的一个规范正交基.
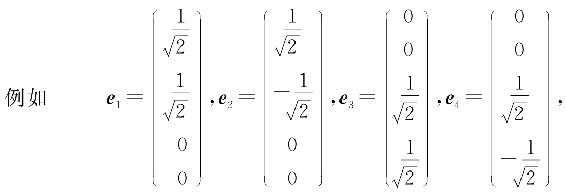
就是R4的一个规范正交基.
设向量组a1，a2，…，ar是向量空间V的一个基，求V的一个规范正交基. 这也就是要找一组两两正交的单位向量组el，e2，…，er，使e1，e2，…，er与a1，a2，…，ar等价. 这样的问题，称为将a1，a2，…，ar，这个基规范正交化.
我们可以用以下步骤将a1，a2.…ar规范正交化，取
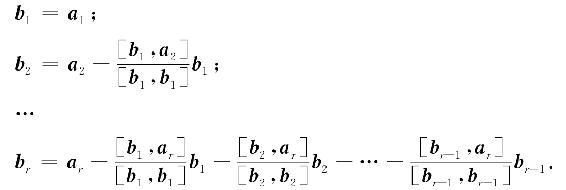
验证可知b1，b2，…，br两两正交，且b1，b2，…，br与a1，a2，…，ar等价，
然后再对b1，b2，…，br单位化，得
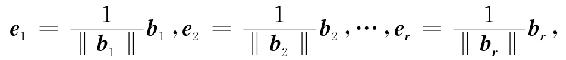
即为V的一个规范正交基.
上述从线性无关向量组a1，a2，…，ar导出正交向量组b1，b2，…，br的过程称为施密特（Schimidt）正交化过程.
例5.2 设向量a1=（1，1，0，0）T，a2=（0，1，1，0）T，a3=（1，0，1，0）T，试把这组向量规范正交化.
解 先正交化：
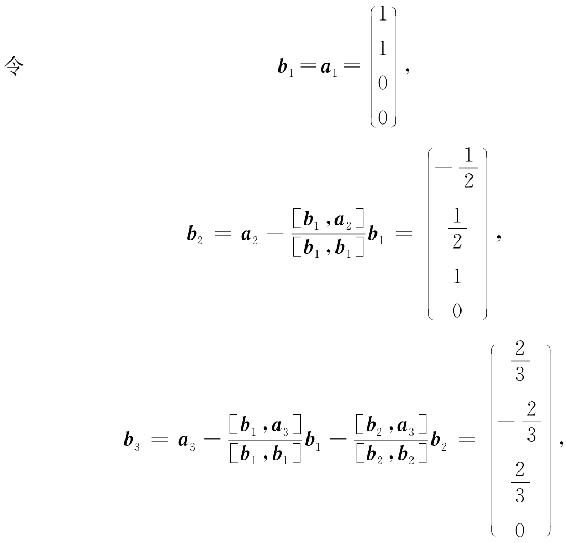
再单位化：取
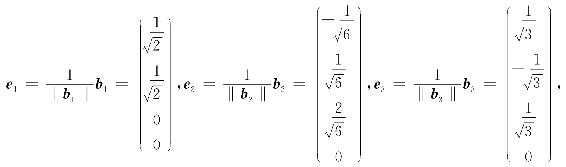
则e1，e2，e3即为所求.
例5.3 已知a1=（1，1，1）T，求一组非零向量a2，a3使a1，a2，a3两两正交.
解 依题意a2，a3满足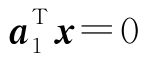
，即有
x1+x2+x3=0，
它的基础解系为
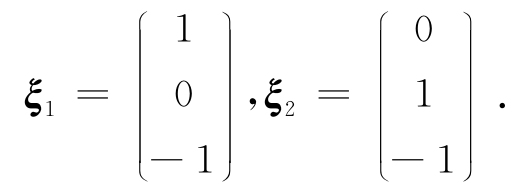
把ξ1，ξ2，正交化，取
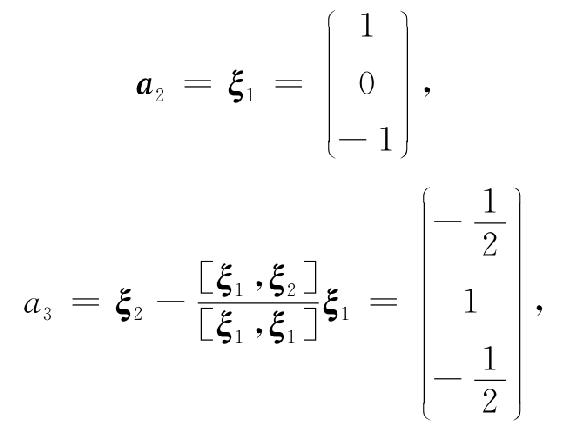
则a1，a2，a3两两正交.
5.1.4 正交矩阵与正交变换
定义5 若n阶方阵A满足
ATA=E（或AAT=E），
则称A为正交矩阵，简称正交阵.
定理2 n阶方阵A为正交阵的充分必要条件是A的n个列（行）向量都是单位向量，且两两正交.
证 设n阶方阵A的n个列向量为a1，a2，...，an. 即A=（a1，a2，…an），由于ATA=E，即有
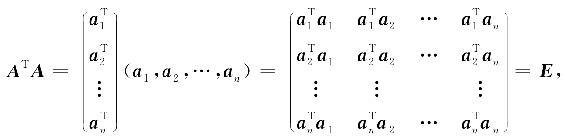
亦即
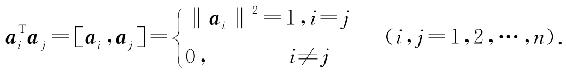
所以A的n个列向量都是单位向量，且两两正交.
又因为AAT=E，所以同理可证，A的n个行向量都是单位向量，且两两正交.
正交矩阵的性质：
（i）若A为正交矩阵，则A可逆，且A-1=AT；
（ii）若A为正交矩阵，则|A|＝±1；
（iii）若A与B均为正交矩阵，则AB也是正交矩阵：
（iv）若A为正交矩阵，则AT，A-1，Ak（k为整数）也是正交矩阵.
定义6 若P为正交矩阵，则称线性变换y=Px为正交变换.
正交变换的性质：
（i）正交变换保持任意两个向量的内积不变；
（ii）正交变换保持向量的长度不变；
（iii）正交变换保持两个向量之间的距离不变；
（iv）正交变换保持两个向量的夹角不变.