习题5

习题5

1. 计算下列向量α，β的内积：

（1）α=（-1，0，3，-5）T，β=（4，-2，0，1）T；

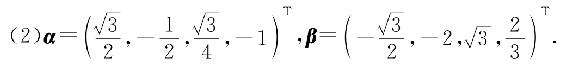
2. 设a=（1，0，-2）T，b=（-4，2，3）T，c与a正交，b=λa+c，求λ，c.

3. 证明如果向量β与向量α1，α2都正交，则β与α1，α2的任一线性组合也正交.

4. 证明如果Rn中向量α与Rn中任意向量都正交，则α必是零向量.

5. 把下列向量组规范正交化：

（1）α1=（1，-2，-2）T，α2=（-1，0，1）T，α3=（5，-3，7）T；

（2）α1=（1，1，1，1）T，α2=（3，3，-1，1）T，α3=（-2，0，6，8）T.

6. 判断下列矩阵是否为正交矩阵：

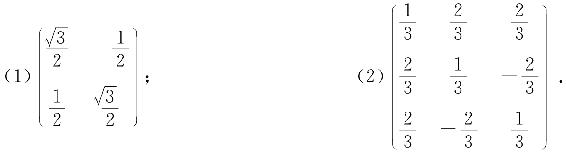
7. 求下列方阵的特征值和特征向量：

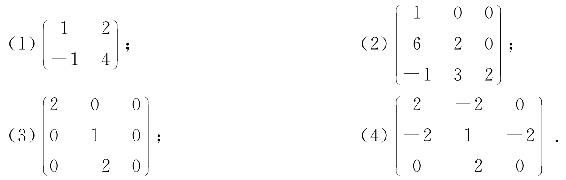
8. 设n阶矩阵A，B满足R（A）+R（B）<n，证明A与B有公共的特征值，有公共的特征向量.

9. 已知A2+2A-3E=0，证明A的特征值只可能为-3或1.

10. 设A为正交矩阵，且|A|＝-1，证明λ＝-1是A的特征值.

11. 设k是m阶矩阵Am×nBn×m的特征值，证明λ也是n阶矩阵BA的特征值.

12. 已知3阶矩阵A的特征值为1，2，3，求|A3-5A2+7A|.

13. 已知3阶矩阵A的特征值为1，-1，2，求|A*-2A+3E|.

14. 设矩阵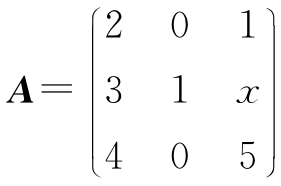可相似对角化，求x.

15. 已知的一个特征向量，

（1）求参数a，b及特征向量p所对应的特征值；

（2）问A能不能相似对角化？并说明理由.

16. 试求一个正交的相似变换矩阵，将下列对称矩阵化为对角矩阵：

17. 设矩阵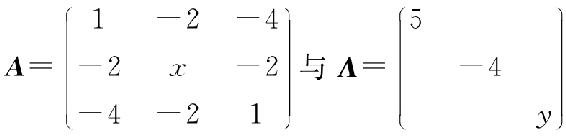相似，求x，y；并求一个正交矩阵P，使P-1AP=A.

18. 设3阶矩阵A的特征值为. λ1=2，k2＝-2，λ3=1；对应的特征向量依次为

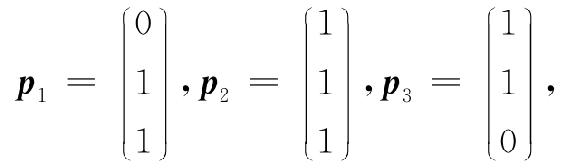
求A.

19. 设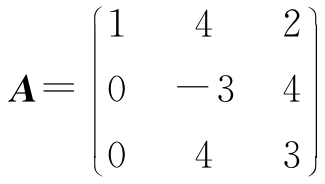，求A100.