2.4 矩阵的分块

2.4　矩阵的分块

对于行数和列数较高的矩阵，运算时常采用分块法，使大矩阵的运算转化为小矩阵的运算. 将矩阵用若干条纵线和横线分成若干个小矩阵，每个小矩阵称为原矩阵的子块，以子块为元素的形式上的矩阵称为分块矩阵.

例如

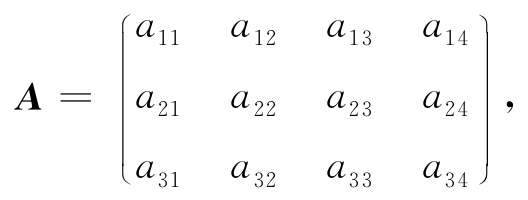
可如下分块：

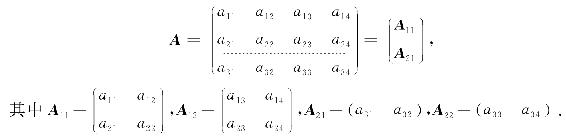
一个矩阵可以按不同的方式分块，上述矩阵A也可如下分块：

其中，aj=（a1j，a2j，…，amj）T，j=1，2，…，n.

由此可见，矩阵的分块方式很多，究竟采用哪种方式分块，要根据矩阵的具体运算来确定.

分块矩阵的运算：分块后的矩阵，把小矩阵当成元素，按普通矩阵的运算法则进行运算.

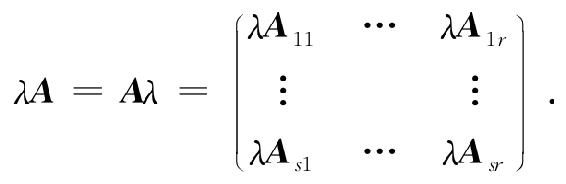
①设矩阵A与B是同型矩阵，且采用相同的分块法，得分块矩阵为

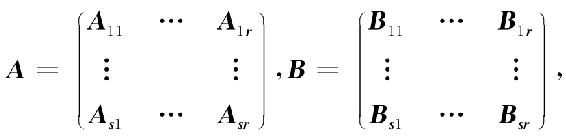
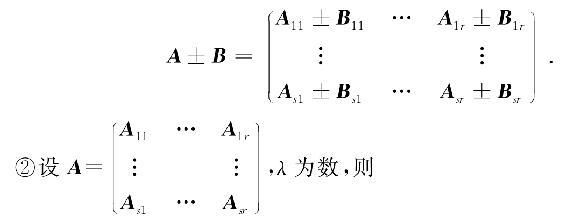
其中，各对应的子块Aij与Bij具有相同的行数和列数，则

③设A为m×l矩阵，B为l×n矩阵，分块为

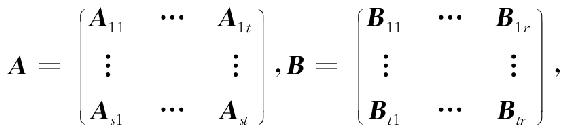
此处A的列的分法与B的行的分法一致，即Ai1，A=i2，…，Ait的列数分别等于B1j，B2j，…，Btj的行数，则

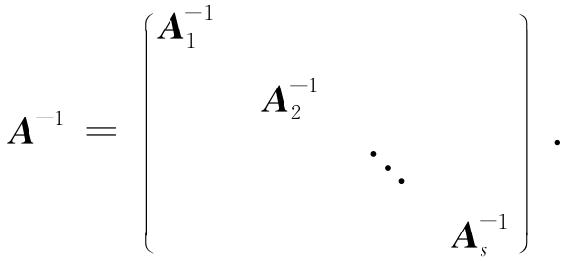
其中，只有在对角线上有非零子块，其余的子块都为零矩阵，且在对角线上的子块都是方阵，此时称A为分块对角矩阵，并有

（i）|A|=|A1||A2|…|As|；

（ii）当|Ai|≠0（i=1，…，s）时，有

若

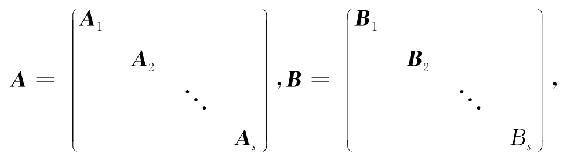
是两个分块对角矩阵，其中Ai与Bi是同阶方阵，则

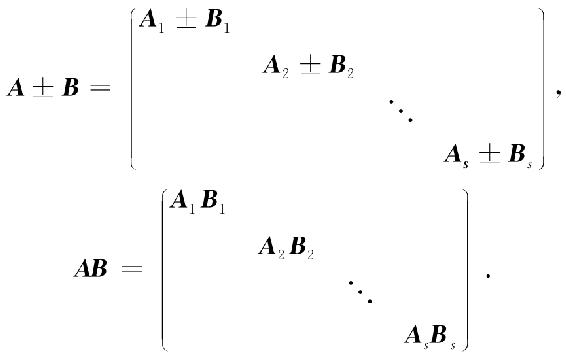
由此可见，对于能划分为分块对角矩阵的矩阵，如果采用分块米求逆阵或进行运算是十分方便的.

例2.12　设

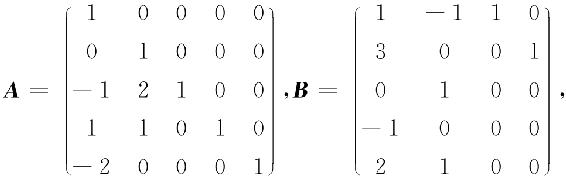
求AB.

解

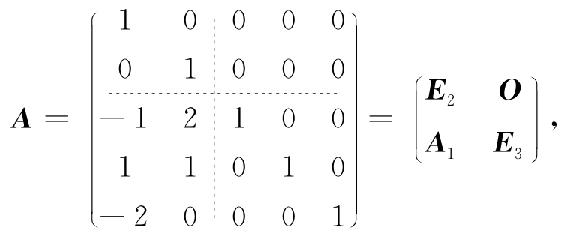
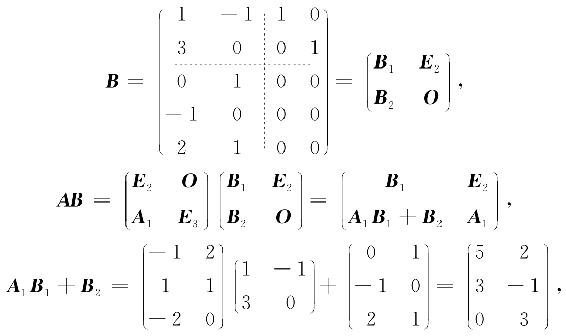
所以

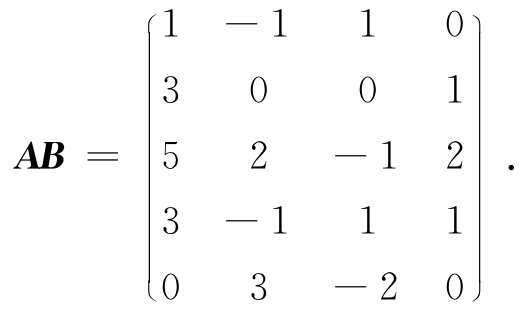
例2.13　设

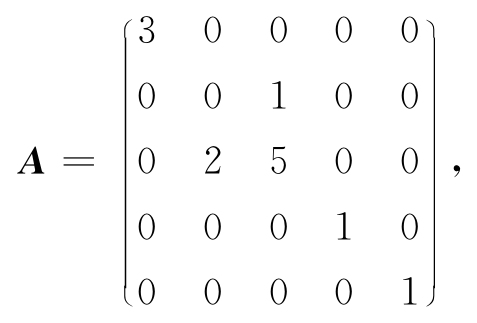
求A-1.

解　将A分块如下：

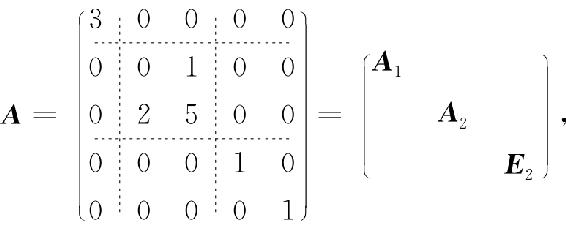
其中

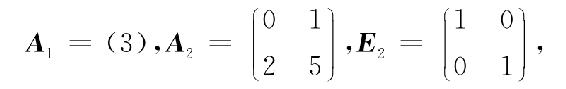
由于

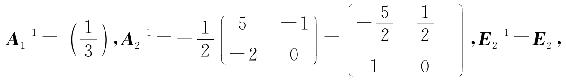
所以

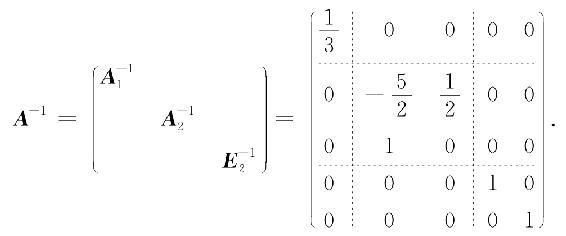
例2.14　设A，C分别为r阶和s阶可逆矩阵，求分块矩阵

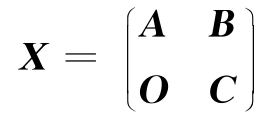
的逆矩阵.

解　设逆矩阵分块为

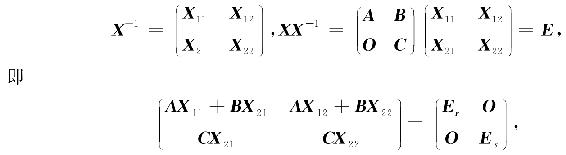
比较等式两边对应的子块，有

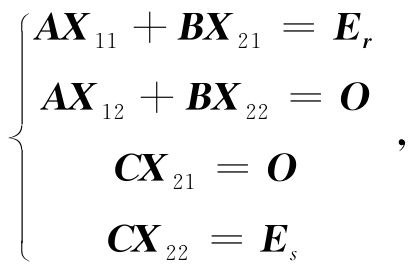
注意到A，C可逆，可解得

X22 =C-1，X21=O，X11=A-1，X12＝-A-1BC-1，

所以

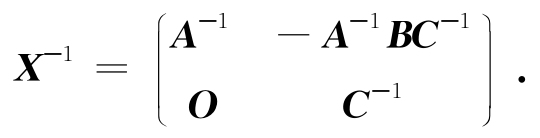
对于线性方程组

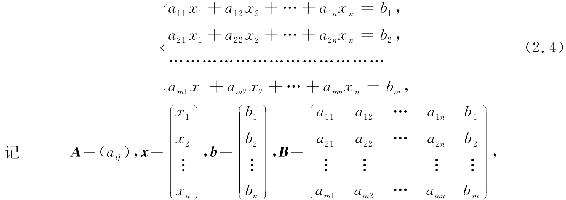
其中，A称为系数矩阵，x称为未知数向量，b称为常数项向量，B称为增广矩阵. 按矩阵的分块法，可记

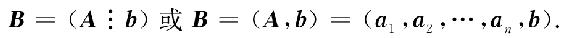
利用矩阵的乘法，此方程组可记作

Ax=b.

（2.5）

方程（2.5）以向量x为未知元，它的解称为方程组（2.4）的解向量.

若把系数矩阵A按行分块，则线性方程组Ax=b可记作

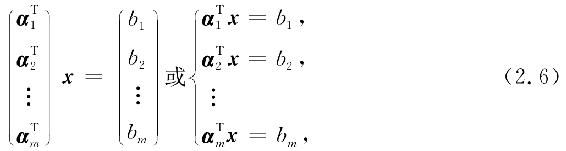
这相当于把每个方程

ai1x1+ai2x2+…+ainxn=bi

记作

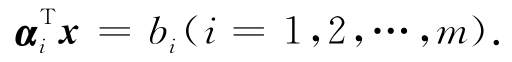
若把系数矩阵A按列分块，则与A相乘的x应对应按行分成n块，则线性方程组Ax=b可记作

即

a1x1+a2x2+…+anxn=b.

（2.7）

方程组（2.5）（2.6）（2.7）是线性方程组（2.4）的各种变形，都表示线性方程组，以后将混同使用不加区分.