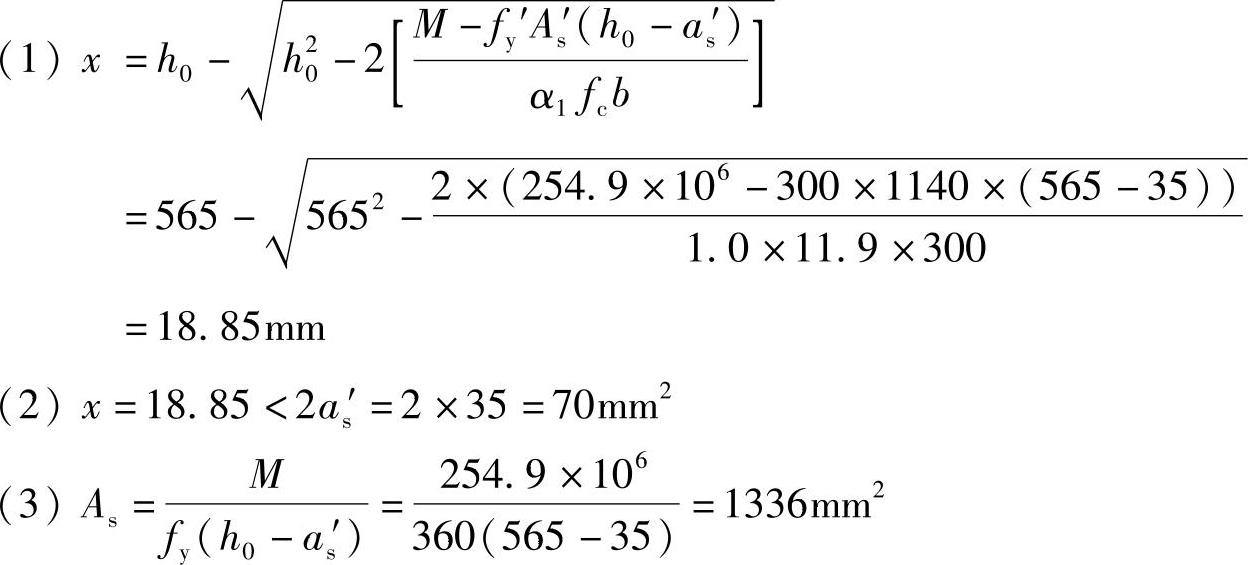矩形梁的受弯承载力
(一)考试要求
1.《考试大纲》的要求:掌握
2.“试题”回顾
(1)梁的破坏形态
【试题3.2.1】 单筋梁的破坏形态(1998年)
某矩形截面的简支梁b×h=200mm×500mm,混凝土强度等级为C20,跨中受拉区配置4 20的热轧Ⅱ级钢筋(单筋梁)。当梁正截面破坏时,属于下列何种情况?
20的热轧Ⅱ级钢筋(单筋梁)。当梁正截面破坏时,属于下列何种情况?
提示:该梁平衡配筋率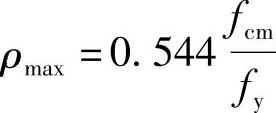
(A)界限破坏 (B)适筋破坏 (C)少筋破坏 (D)超筋破坏
【试题3.2.2】 混凝土受压区高度对梁的影响(1999年)
在受弯构件正截面承载力计算中,混凝土受压区高度x>ξbh0,该梁属于下列何项所示?
(A)无筋梁 (B)少筋梁 (C)适筋梁 (D)超筋梁
【试题3.2.3】 各类梁的特性(1999年)
在下列表述中何项错误?
(A)少筋梁受弯时钢筋应力过早超过屈服点,引起梁的脆性破坏,因此不安全
(B)适筋梁破坏前有明显预兆,经济性与安全性均较好
(C)超筋梁过于安全,不经济
(D)在截面高度受限制时,可采用双筋梁
(2)单筋梁
【试题3.2.4】 单筋梁的配筋量As(1998年)
有一等截面的钢筋混凝土梁,受某种工况荷载(设计值)的作用,如图3.2.1所示。该矩形梁截面bmm×hmm,钢筋及混凝土材料已定,按单筋梁配置。试问B支座的配筋量As应为下列何项所示?式中γs为内力臂系数。
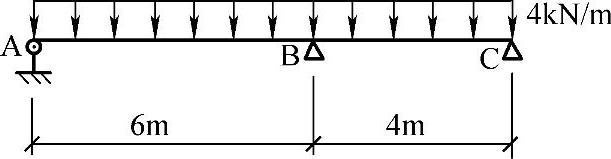
图 3.2.1
【试题3.2.5】 单筋梁的弯矩设计值(2003年)
北京某露天敞开的钢筋混凝土结构,有一矩形截面简支梁,它的截面尺寸和配筋如图3.2.2所示。安全等级二级。梁采用C40混凝土,单筋矩形梁,纵向受力筋采用HRB335,已知相对受压区高度ξ=0.1726,试问,该梁能承受的非地震组合的弯矩设计值MC与下列何项数值最为接近?
(A)140.32 (B)158.36
(C)144.91 (D)151.61
【试题3.2.6】 雨篷梁的受弯承载力(2005年)
某多层办公楼为现浇钢筋混凝土框架结构,抗震等级为二级,混凝土强度等级为C30,梁、柱纵向钢筋采用HRB335级钢筋,梁、柱箍筋采用HPB235级钢筋。其首层入口处雨篷的平面图与剖面图如图3.2.3所示。
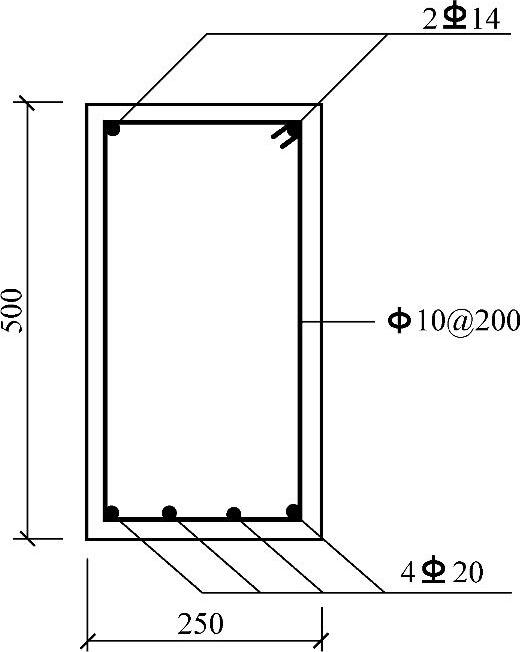
图 3.2.2
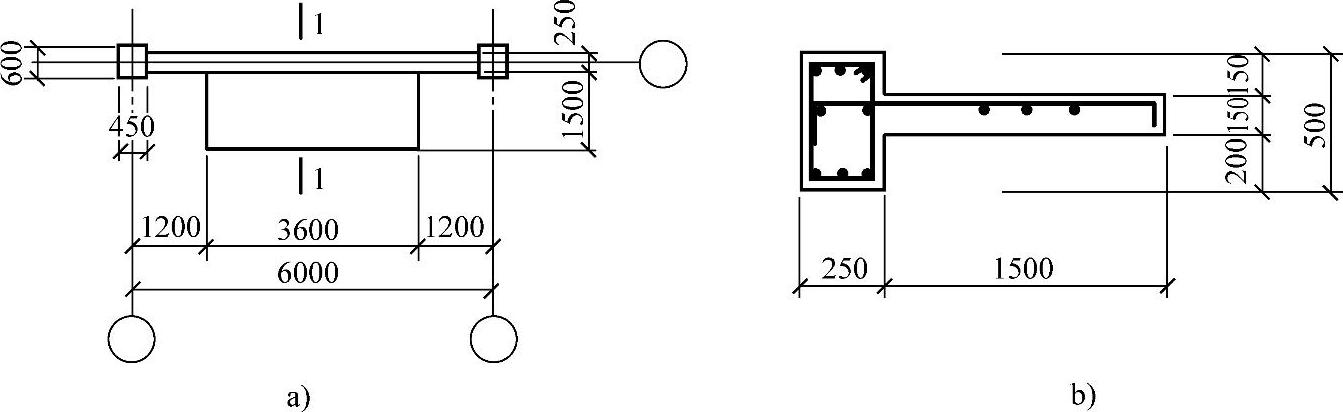
图 3.2.3
a)雨篷平面图 b)1-1剖面图
已知雨篷梁截面尺寸b×h=250mm×500mm。假定仅为满足受弯条件所需跨中及支座实配的纵向受拉钢筋均为3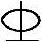 22(As=As′=1140mm2),as=as′=35mm,ξb=0.55;不考虑地震作用组合。当不考虑梁跨中纵向受压钢筋的影响时,试问,相应的雨篷梁跨中正截面受弯承载力设计值M(kN·m),应与下列何项数值最为接近?
22(As=As′=1140mm2),as=as′=35mm,ξb=0.55;不考虑地震作用组合。当不考虑梁跨中纵向受压钢筋的影响时,试问,相应的雨篷梁跨中正截面受弯承载力设计值M(kN·m),应与下列何项数值最为接近?
(A)95 (B)143
(C)217 (D)242
【试题3.2.7】 楼梯梁的受弯承载力(2006年)
楼梯梁TL-1及楼梯柱TZ-1的计算简图如图3.2.4所示。楼梯梁截面尺寸b×h=300mm×350mm,as=as′=40mm,ξb=0.55;当进行抗弯设计时,所需的梁顶纵向受拉钢筋为3 18(As=763mm2)。试问,当不考虑梁底配置的纵向受压钢筋作用时,TL-1支座处的受弯承载力设计值M(kN·m),与以下何项数值最为接近?
18(As=763mm2)。试问,当不考虑梁底配置的纵向受压钢筋作用时,TL-1支座处的受弯承载力设计值M(kN·m),与以下何项数值最为接近?
(A)64.8 (B)76.3
(C)78.3 (D)87.6
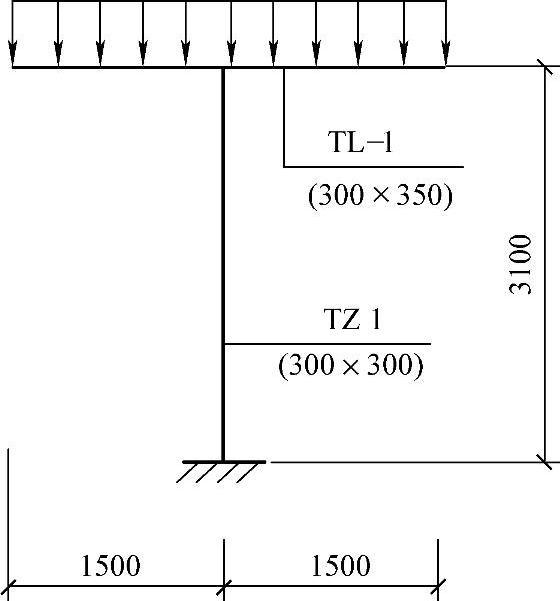
图 3.2.4
【试题3.2.8】 框架梁的配筋(2007年)
现浇框架梁KL2的截面尺寸b×h=300mm×550mm,考虑地震作用组合的梁端最大负弯矩设计值M=150kN·m,as=as′=40mm,ξb=0.35。试问,当按单筋梁计算时,该梁支座顶面纵向受拉钢筋截面面积As(mm2),应与下列何项数值最为接近?
(A)1144 (B)1452 (C)1609 (D)1833
【试题3.2.9】 屋面板的配筋(2010年)
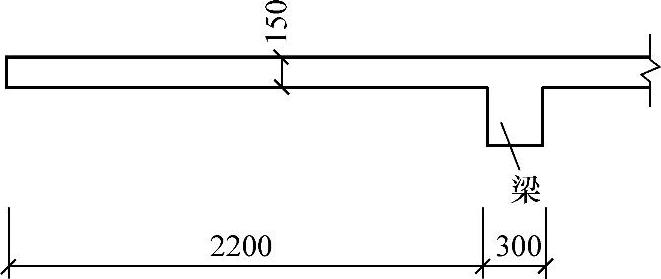
图 3.2.5
某钢筋混凝土不上人屋面挑檐剖面如图3.2.5所示,屋面板混凝土强度等级采用C30。屋面面层荷载相当于100mm厚水泥砂浆的重量,梁的转动忽略不计。板受力钢筋保护层厚度c=20mm。假设挑檐板根部每米板宽的弯矩设计值M=20kN·m,采用HRB335级钢筋,试问,每米板宽范围内按受弯承载力计算所需配置的钢筋面积As(mm2),与下列何项数值最为接近?
提示as=25mm;受压区高度按实际计算值确定。
(A)470 (B)560 (C)620 (D)670
【试题3.2.10】 悬挑板的配筋(2010年)
某滨海风景区体育建筑中的钢筋混凝土悬挑板疏散外廊如图3.2.6所示。挑板及栏板建筑面层做法为双面抹灰各20mm。混凝土容重25kN/m3,抹灰容重20kN/m3。混凝土强度等级为C30,受力钢筋采用HRB335级( ),分布钢筋采用HPB235级(
),分布钢筋采用HPB235级( )。若该悬挑板按每延米宽计算的支座负弯矩设计值M=27kN·m,主筋采用
)。若该悬挑板按每延米宽计算的支座负弯矩设计值M=27kN·m,主筋采用 12钢筋,试问,当按单筋板计算时,该悬挑板的支座负弯矩钢筋配置,选用下列何项最为合适?
12钢筋,试问,当按单筋板计算时,该悬挑板的支座负弯矩钢筋配置,选用下列何项最为合适?
(A) 12@200 (B)
12@200 (B) 12@150
12@150
(C) 12@100 (D)
12@100 (D) 12@75
12@75
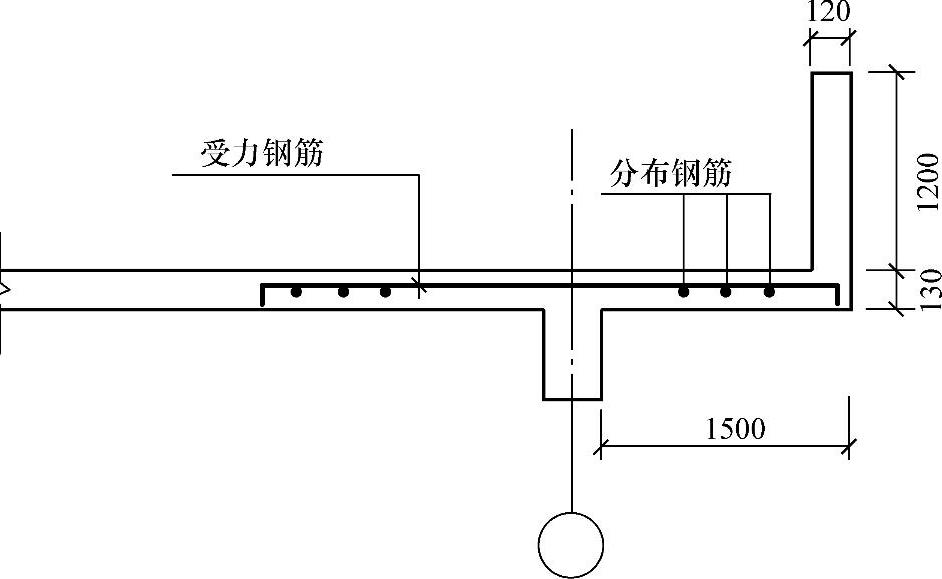
图 3.2.6
(3)双筋梁
【试题3.2.11】 双筋梁的受拉纵筋面积(2002年)
有一根钢筋混凝土连续梁,结构安全等级为二级,混凝土强度等级为C30,纵向钢筋为Ⅲ级钢、箍筋为I级钢,梁截面尺寸b×h=250mm×500mm,如图3.2.7所示,假定梁支座截面配有受压钢筋As′=628mm2,as=as′=40mm,在弯矩设计值M=-280kN·m作用下,试问,该梁支座截面的受拉钢筋截面面积As(mm2)与下列何项数值最为接近?
(A)1700 (B)2226
(C)1898 (D)2052
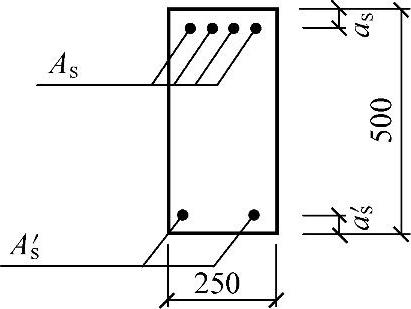
图 3.2.7
【试题3.2.12】 双筋梁的受拉纵筋面积(2003年)
某商场内一钢筋混凝土刚架,如图3.2.8所示,混凝土强度等级为C40,横梁断面尺寸b×h=200mm×550mm,纵筋采用HRB335,假定根据计算,悬挑梁BC梁底部配置2根直径18mm的受压钢筋,若已知混凝土相对受压区高度ξ=0.166,a=a′=40mm。试问,当考虑受压钢筋作用时,上部的受拉钢筋面积(mm2)应与下列何项数值最为接近?
(A)1083 (B)1485
(C)1587.5 (D)2184.5
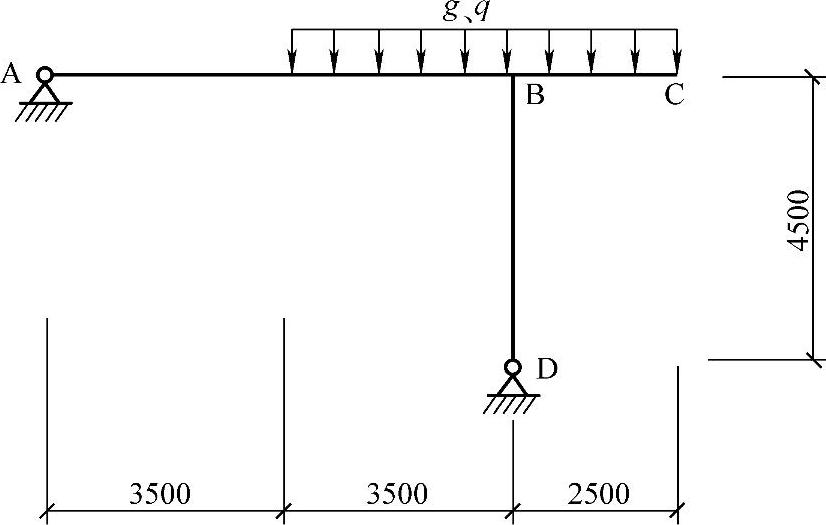
图 3.2.8
【试题3.2.13】 双筋梁的受弯承载力(2004年)
一现浇钢筋混凝土多层框架房屋结构,已知各层层高均为3.6m,梁、柱混凝土强度等级均为C30,fc=14.3N/mm2,ft=1.43N/mm2;梁、柱箍筋采用HPB235级热轧钢筋,fy=210N/mm2。
已知框架梁KL1的抗震等级为二级,在进行某梁端截面设计时,计入梁底受压钢筋为3 25,试问,该截面能承受的最大负弯矩设计值(kN·m),与下列何项数值最为接近?
25,试问,该截面能承受的最大负弯矩设计值(kN·m),与下列何项数值最为接近?
提示:纵向受拉钢筋合力点、纵向受压钢筋合力点至截面近边的距离as=as′=35mm。
(A)395.35 (B)629.6 (C)555.1 (D)545.2
【试题3.2.14】 框架梁的受弯承载力(2011年)
假定,现浇框架梁KL1的截面尺寸b×h=600mm×1200mm,混凝土强度等级为C35,纵向受力钢筋采用HRB400级,梁端底面实配纵向受力钢筋面积As′=4418mm2,梁端顶面实配纵向受力钢筋面积As=7592mm2,h0=1120mm,as′=45mm,ξb=0.55。考虑受压区受力钢筋作用,梁端承受负弯矩的正截面抗震受弯承载力设计值M(kN·m)与下列何项数值最为接近?
(A)2300 (B)2700 (C)3200 (D)3900
(二)《混凝土结构设计规范》规定和算例
1.《混凝土结构设计规范》规定
6.2.10 矩形截面或翼缘位于受拉边的倒T形截面受弯构件,其正截面受弯承载力应符合下列规定(图6.2.10):
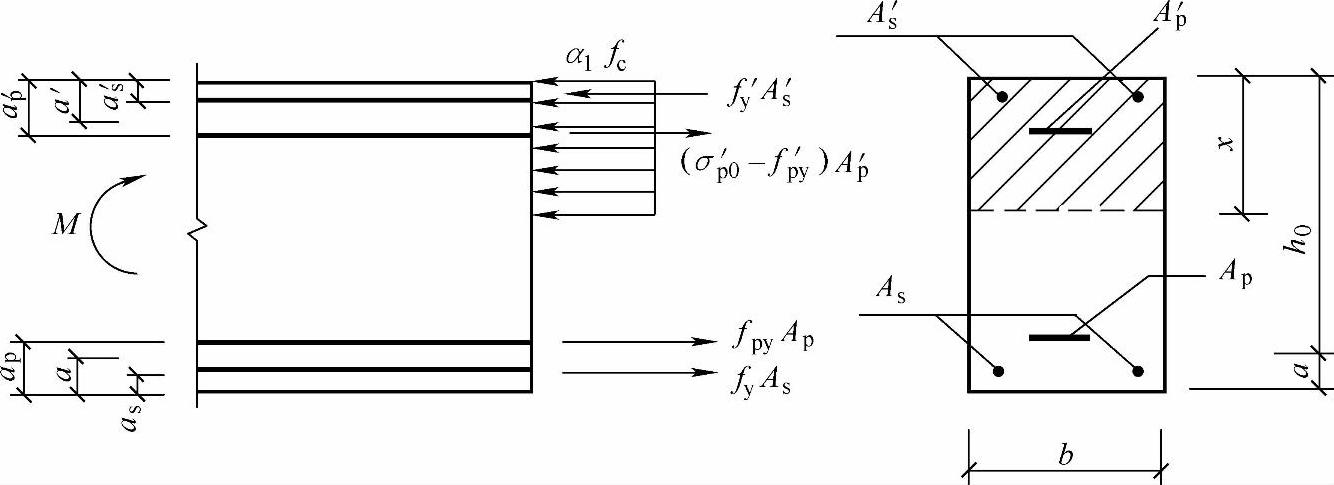
图6.2.10 矩形截面受弯构件正截面受弯承载力计算
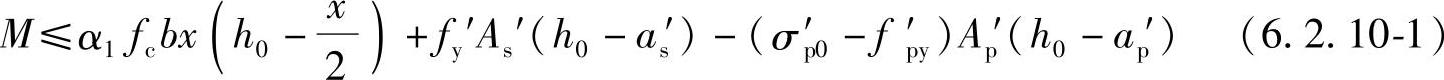
混凝土受压区高度应按下列公式确定:
α1fcbx=fyAs-fy′As′+fpyAp+(σ′p0-f′py)Ap′ (6.2.10-2)
混凝土受压区高度尚应符合下列条件:
x≤ξbh0 (6.2.10-3)
x≥2a′ (6.2.10-4)
式中 M——弯矩设计值;
α1——系数,按本规范第6.2.6条的规定计算;
fc——混凝土轴心抗压强度设计值,按本规范表4.1.4-1采用;
As、As′——受拉区、受压区纵向普通钢筋的截面面积;
Ap、Ap′——受拉区、受压区纵向预应力筋的截面面积;
σp′0——受压区纵向预应力筋合力点处混凝土法向应力等于零时的预应力筋应力;
b——矩形截面的宽度或倒T形截面的腹板宽度;
h0——截面有效高度;
as′、ap′——受压区纵向普通钢筋合力点、预应力筋合力点至截面受压边缘的距离;
a′——受压区全部纵向钢筋合力点至截面受压边缘的距离,当受压区未配置纵向预
应力筋或受压区纵向预应力筋应力(σp′0-f′py)为拉应力时,公式(6.2.10-4)中的a′用as′代替。
6.2.14 当计算中计入纵向普通受压钢筋时,应满足本规范公式(6.2.10-4)的条件;当不满足此条件时,正截面受弯承载力应符合下列规定:
M≤fpyAp(h-ap-as′)+fyAs(h-as-as′)+(σ′p0-f′py)Ap′(ap′-as′) (6.2.14)
式中 as、ap——受拉区纵向普通钢筋、预应力筋至受拉边缘的距离。
2.单筋梁的正截面受弯承载力
(1)承载力计算
基本资料:已知截面尺寸b、h,材料强度fc、ft、fy,钢筋面积As,确定需用的计算参数α1、h0、ξb。
计算步骤:
1)根据《混凝土结构设计规范》第8.5.1条,验算As≥ρminbh,满足要求则进入下一步。此处:
ρmin=max{0.2,45ft/fy}%
2)求压区高度x,由《混凝土结构设计规范》式(6.2.10-2)α1fcbx=fyAs,得到
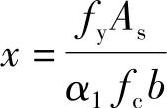
3)根据《混凝土结构设计规范》式(6.2.10-3)验算压区高度x,此时x可能出现如下二种情况:
若x≤ξbh0,则转入下面4)①;
若x>ξbh0,则转入下面4)②。
4)确定受弯承载力Mu
①根据《混凝土结构设计规范》式(6.2.10-1)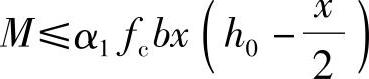 ,求出受弯承载力Mu。
,求出受弯承载力Mu。
②根据《混凝土结构设计规范》式(6.2.10-1)求受弯承载力Mu,取x=ξbh0。得到
Mu=α1fcbh20ξb(1-0.5ξb)
【例3.2.1】 确定单筋矩形截面简支梁的受弯承载力
条件:已知梁的截面尺寸b=200mm,h=500mm,计算跨度l0=4.2m,混凝土强度等级为C30,纵向受拉钢筋为3 20,HRB400级钢筋,环境类别为一类。
20,HRB400级钢筋,环境类别为一类。
要求:求此梁所能承受的弯矩。
答案:基本数据:
由《混规》表4.1.4查得:fc=14.3N/mm2,ft=1.43N/mm2;
由《混规》表4.2.3-1查得fy=360N/mm;
由《混规》第6.2.6条查得α1=1.0;
由《混规》第6.2.7条计算得ξb=0.518;
由《混规》表8.2.1查得,混凝土保护层最小厚度c=20mm,则取as=35mm,h0=h-as=500-35=465mm;
由《混规》附录A查得,As=942mm2。
(1)根据《混规》第8.5.1条验算最小配筋率
ρmin取0.002和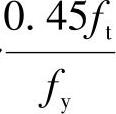 中较大值,
中较大值,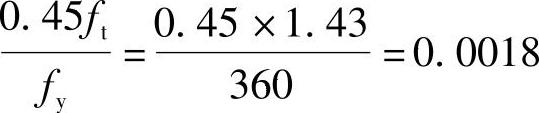 故ρmin=0.002
故ρmin=0.002
Asmin=ρminbh=0.002×200×500=200mm2
As=942mm2>Asmin=200mm2,满足要求。
(2)求压区高度x
由《混规》式(6.2.10-2)α1fcbx=fyAs得:
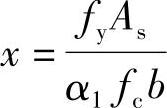
将相关数据代入得:
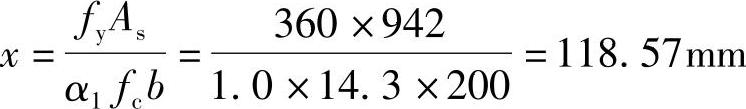
(3)验算压区高度
由《混规》式(6.2.10-3)得:
x=118.5mm<ξbh0=0.518×465mm=240.9mm
满足要求。
(4)计算截面所能承受的弯矩设计值Mu
由《混规》式(6.2.10-1)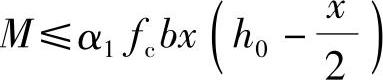 ,将相关数据代入,得:
,将相关数据代入,得:
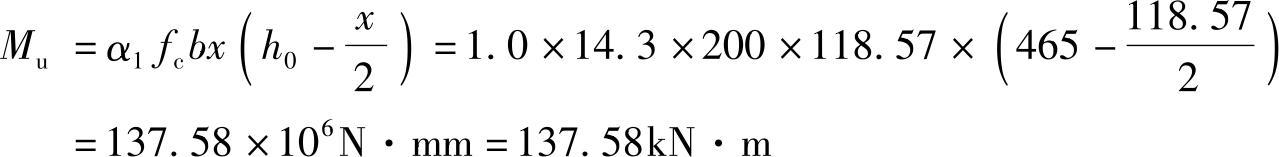
(2)配筋计算
基本资料:已知截面尺寸b、h;材料强度fc、ft、fy;确定需用的计算参数α1、h0、ξb;荷载效应M
计算步骤:
1)求压区高度x,由《混凝土结构设计规范》式(6.2.10-1)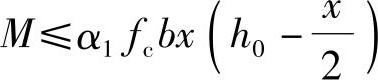 得到
得到
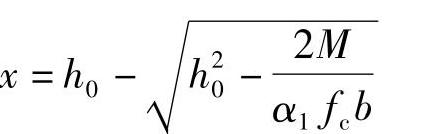
2)根据《混凝土结构设计规范》式(6.2.10-3),验算压区高度x<ξbh0,如满足要求则进入下一步。
3)求受拉钢筋面积As,由《混凝土结构设计规范》式(6.2.10-2)α1fcbx=fyAs,得到
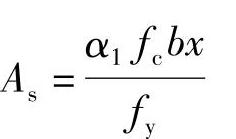
4)根据《混凝土结构设计规范》第8.5.1条,验算As≥ρminbh,当As<ρminbh时取As=ρminbh。此处
ρmin=max(0.2,45ft/fy)%
【例3.2.2】 矩形截面单筋梁的配筋计算
条件:已知矩形梁截面尺寸b×h=250mm×500mm,安全等级二级,环境类别为一类,弯矩设计值为M=150kN·m,混凝土强度等级为C30,钢筋采用HRB400级钢筋。
要求:所需的受拉钢筋截面面积。
答案:由《混规》表4.1.4,表4.2.3-1,查得fc=14.3N/mm2,ft=1.43N/mm2,fy=360N/mm2。
由《混规》第6.2.6条、第6.2.7条知,α1=1.0,β1=0.8,求得ξb=0.518。
由《混规》第8.2.1条,可知c=20mm,
故设as=35mm,h0=500-35=465mm。
(1)求压区高度x
由《混规》式(6.2.10-1)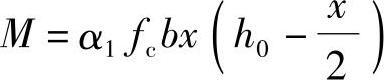 解得
解得
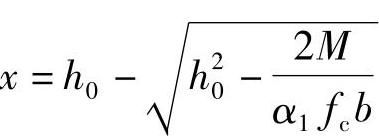
代入相关数据解得
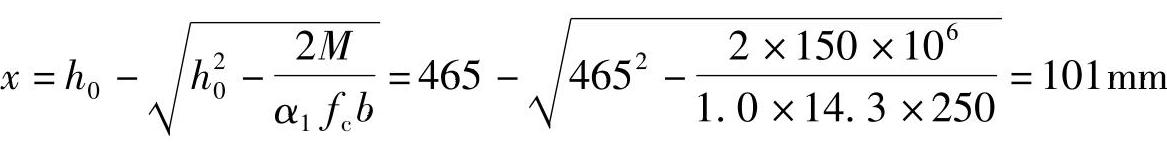
(2)验算压区高度x
根据《混规》式(6.2.10-3),x≤ξbh0
x=101mm<ξbh0=0.518×465=240.9mm,满足要求。
(3)求受拉钢筋面积As
由《混规》式(6.2.10-2),α1fcbx=fyAs
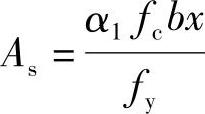
代入相关数据
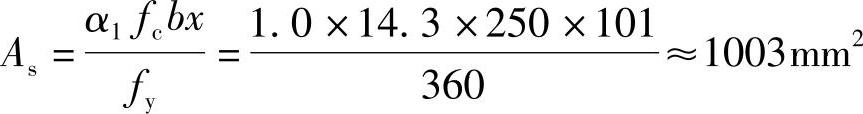
(4)验算受拉钢筋最小配筋率
由《混规》第8.5.1条,As≥ρminbh,当As<ρminbh取As=ρminbh
此外,ρmin取0.002和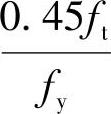 两者中的较大值
两者中的较大值
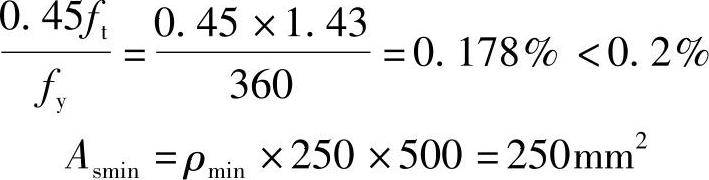
As=1207mm2>Asmin=250mm2
满足要求。
3.双筋梁的正截面受弯承载力
(1)承载力计算
基本资料:已知截面尺寸b、h,材料强度fc、ft、fy,钢筋面积As、As′,确定需用的计算参数α1、h0、ξb。
1)求压区高度x,由《混凝土结构设计规范》式(6.2.10-2),α1fcbx=fy′As′得
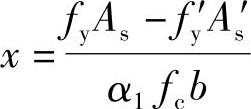
2)根据《混凝土结构设计规范》式(6.2.10-3)、式(6.2.10-4)验算压区高度x,此时x可能出现如下三种情况:
若x<2as′,则转入3)中的①;
若2as′≤x≤ξbh0,则转入3)中的②;
若x>ξbh0,则转入3)中的③。
3)确定受弯承载力Mu
①x<2as′,由《混凝土结构设计规范》式(6.2.14),Mu=fyAs(h0-as′)求得受弯承载力Mu。
②2as′≤x≤ξbh0,由《混凝土结构设计规范》式(6.2.10-1),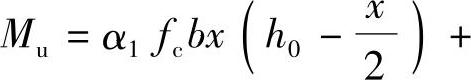
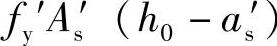 求得受弯承载力Mu。
求得受弯承载力Mu。
③x>ξbh0,由《混凝土结构设计规范》式(6.2.10-1)求受弯承载力Mu,取x=ξbh0得到
Mu=α1fcbh20ξb(1-0.5ξb)+fy′As′(h0-as′)
【例3.2.3】 双筋矩形截面梁的承载力计算(2as′≤x≤ξbh0)
条件:已知梁截面尺寸b=300mm,h=600mm,选用C35的混凝土和HRB400级的纵向钢筋,环境类别为二a类。配有纵向受压钢筋2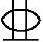 16,受拉钢筋4
16,受拉钢筋4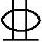 25。
25。
要求:求梁截面所能承受的弯矩设计值Mu。
答案:基本资料由《混规》表4.1.4、表4.2.3-1,查得fc=16.7N/mm2,ft=1.57N/mm2,fy=fy′=360N/mm2。
由《混规》第6.2.6条,查得α1=1.0,
由《混规》第6.2.7条,计算得ξb=0.518
由《混规》第8.2.1条,查得最小保护层厚度c=25mm
取as=as′=40mm,h0=600-40=560mm
由《混规》附录A,As′=402mm2,As=1964mm2
(1)求压区高度x
由《混规》式(6.2.10-2),α1fcbx=fyAs-fy′As′,得:
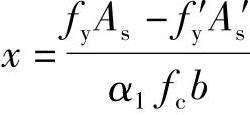
代入相关数据可得
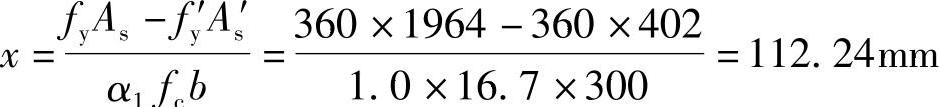
(2)验算压区高度x
根据《混规》式(6.2.10-3)、式(6.2.10-4):
ξbh0=0.518×560=290.08mm
2as′=2×40=80mm
2as′=80mm<x=112.24mm<ξbh0=0.518×560=290.08mm
(3)确定受弯承载力Mu
根据《混规》式(6.2.10-1),将相关数据代入得:
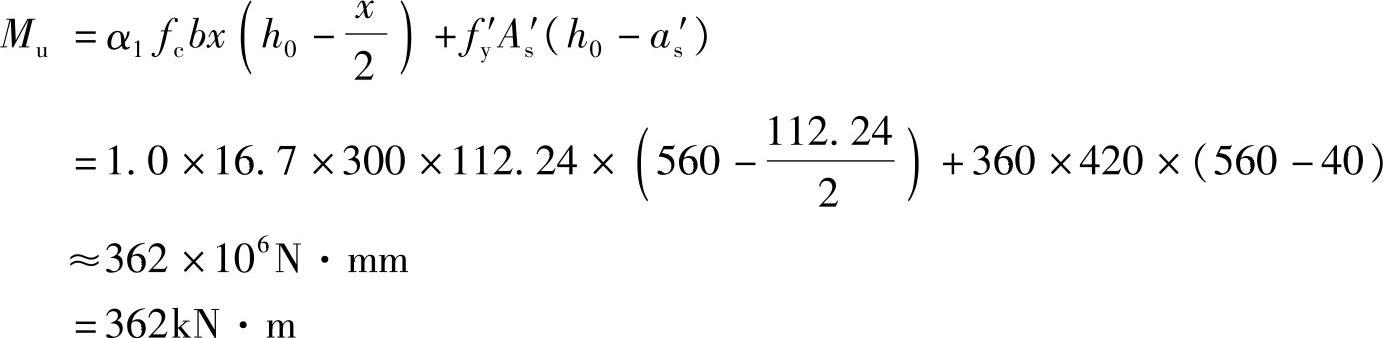
【例3.2.4】 双筋矩形截面梁的承载力计算(x<2as′)
条件:已知条件同【例3.2.3】,但梁中配置的纵向受压钢筋为3 16,受拉钢筋为3
16,受拉钢筋为3 25。
25。
要求:求梁截面所能承受的弯矩设计值Mu。
答案:确定基本数据
由《混规》附录A查得,As′=603mm2,As=1473mm2,其他同【例3.2.3】。
(1)求压区高度x
由《混规》式(6.2.10-2)α1fcbx=fyAs-fy′As′,得到
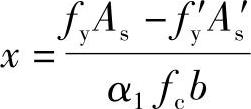
代入相关数据可得
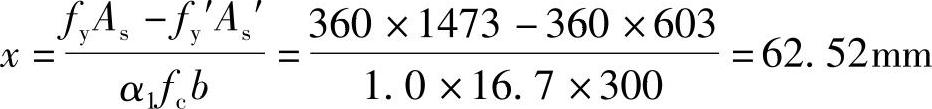
(2)验算压区高度x
由《混规》式(6.2.10-4),x≥2as′
2as′=2×40=80mm>x=62.52mm,不满足此条件
(3)确定受弯承载力Mu
由《混规》式(6.2.14)Mu≤fyAs(h0-as′),得
Mu≤fyAs(h0-as′)=360×1473×(560-40)
=275.75×106N·mm
=275.75kN·m
【例3.2.5】 双筋矩形截面梁的承载力计算(x>ξbh0)
条件:已知条件同【例3.2.3】,但梁中配置的纵向受压钢筋为2 16,受拉钢筋为8
16,受拉钢筋为8 28。
28。
要求:求梁截面所能承受的弯矩设计值Mu。
答案:确定基本数据
由《混规》附录A查得:As′=402mm2,As=4926mm2,取as′=40mm,as=70mm,其他同【例3.2.3】。
(1)求压区高度x
由《混规》式(6.2.10-2),α1fcbx=fyAs-fy′As′解得
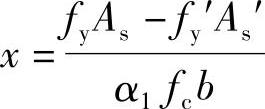
代入相关数据可得
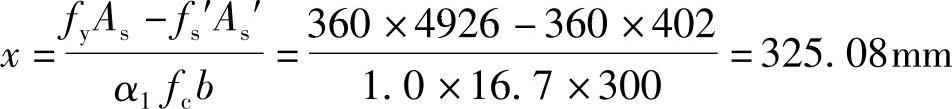
(2)验算压区高度
根据《混规》式(6.2.10-3):
ξbh0=0.518×530=274.54mm<x=325.08mm
(3)确定受弯承载力Mu
由《混规》式(6.2.10-1),取x=ξbh0可得
M=α1fcbh20ξb(1-0.5ξb)+fy′As(h0-as′)
=1.0×16.7×300×5302×0.518×(1-0.5×0.518)+360×402×(530-40)
=611.09×106N·mm
=611.09kN·m
(2)配筋计算
1)已知M,求As、As′
基本资料:已知截面尺寸b、h;材料强度fc、ft、fy;确定需用的计算参数α1、h0、ξb;荷载效应M。
计算步骤:
①求受压钢筋As′,由《混凝土结构设计规范》式(6.2.10-1):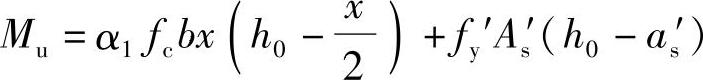 ,求As′。
,求As′。
为了充分发挥混凝土的受压能力,取x=ξbh0得到
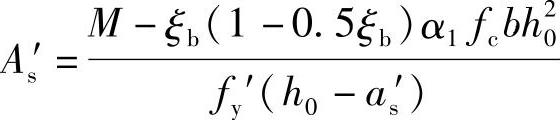
②对As′进行分析,此时可能出现如下两种情况:
若As′≤0,说明不需配置受压受力筋,可按单筋梁计算。
若As′>0,说明需配置受压受力筋,则进入下一步。
③求受拉钢筋As,由《混凝土结构设计规范》式(6.2.10-2),α1fcbx=fyAs-fy′As′,取x=ξbh0,可得到
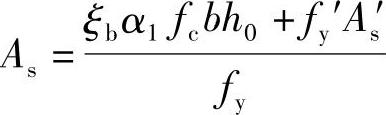
【例3.2.6】 双筋矩形截面梁的截面设计,求As和As′
条件:已知梁截面尺寸b=250mm,h=550mm,选用C30的混凝土和HRB400级的纵向钢筋,环境类别为一类,截面所承受的弯矩设计值M=400kN·m。
要求:求所需的纵向钢筋。
答案:基本数据由《混规》表4.1.4,表4.2.3-1查得,fc=143.3N/mm2,fy=fy′=360N/mm2。
由《混规》第6.2.6条,查得α1=1.0
由《混规》第6.2.7条,计算ξb=0.518
由《混规》表8.2.1,查得混凝土保护层最小厚度为20mm。
因弯矩设计值较大,预计受拉钢筋需排成两排,故取
h0=h-as=550-60=490mm
(1)求受压钢筋As′
由《混规》式(6.2.10-1):
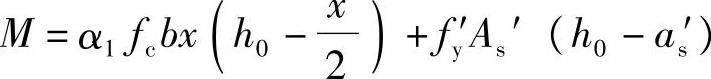
为了充分发挥混凝土的受压能力,取x=ξbh0,得到
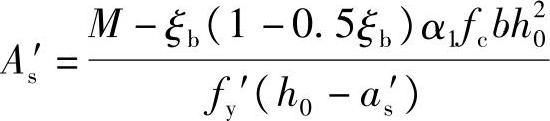
代入相关数据得
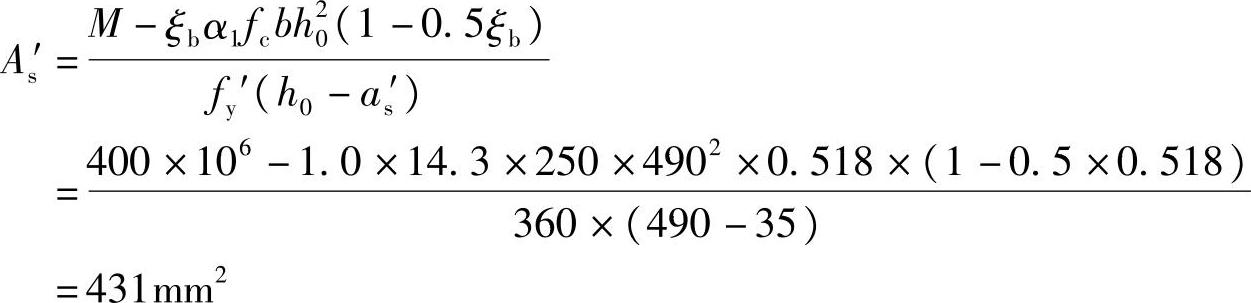
(2)对As′进行分析
因为As′>0说明需要配置受压受力钢筋(当As′≤0时说明不需配受压受力钢筋,应按单筋梁计算)
(3)求受拉钢筋As
由《混规》式(6.2.10-2),α1fcbx=fyAs-fy′As′,x=ξbxh0可得
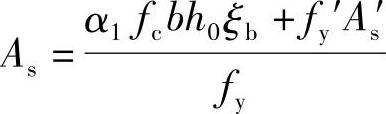
代入相关数据可得
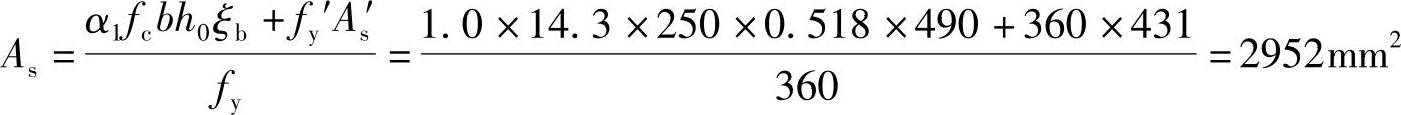
(4)配筋
受压钢筋选3 14(As′=461mm2),受拉钢筋选8
14(As′=461mm2),受拉钢筋选8 22(As=3041mm2),截面配筋如图3.2.9所示。
22(As=3041mm2),截面配筋如图3.2.9所示。
2)已知M和As′,求As
基本资料:已知截面尺寸b、h,材料强度fc、ft、fy,受压钢筋As′;确定需用的计算参数α1、h0、ξb;荷载效应M。
计算步骤:
①求压区高度x,由《混凝土结构设计规范》式(6.2.10-1)得
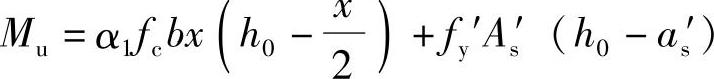
得到
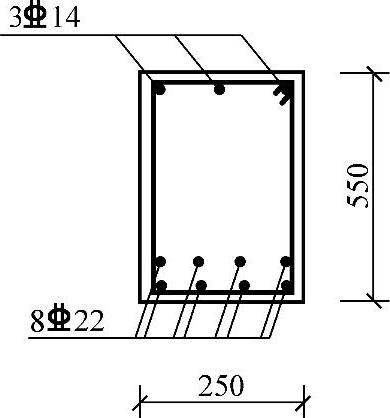
图 3.2.9
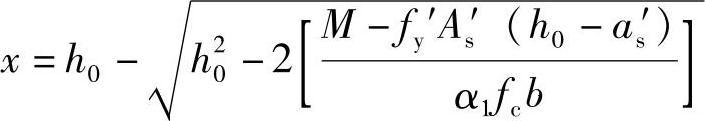
②根据《混凝土结构设计规范》第6.2.10条、式(6.2.10-3)、式(6.2.10-4)验算压区高度x,此时,x可能出现如下三种情况:
若x<2as′,则转入③a;
若2as′≤x≤ξbh0,则转入③b;
若x>ξbh0,则转入③c。
③求受拉钢筋As
a.x<2as′,由《混凝土结构设计规范》式(6.2.14),
Mu=fyAs(h0-as′)
得到
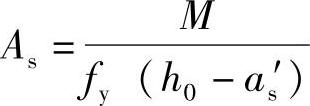
b.2as′≤x≤ξbh0,由《混凝土结构设计规范》式(6.2.10-2),
α1fcbx=fyAs-fy′As′
得到
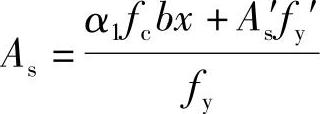
c.x>ξbh0,说明受压钢筋As′太小,应按As′未知,重新计算As′及As。
【例3.2.7】 双筋矩形截面梁的截面设计,As′已知,求
条件:已知条件同【例3.2.6】,但截面的受压区已配置受压钢筋3 22。
22。
要求:求所需的受拉钢筋As。
答案:确定基本数据,由《混规》附录A查得,As′=1140mm2,其他同【例3.2.6】。
(1)求压区高度x
由《混规》式(6.2.10-1):
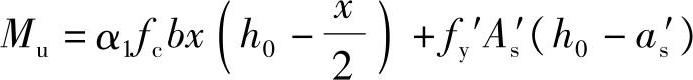
得到
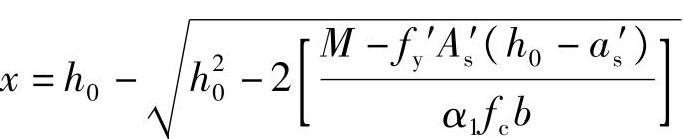
代入相关数据可得:
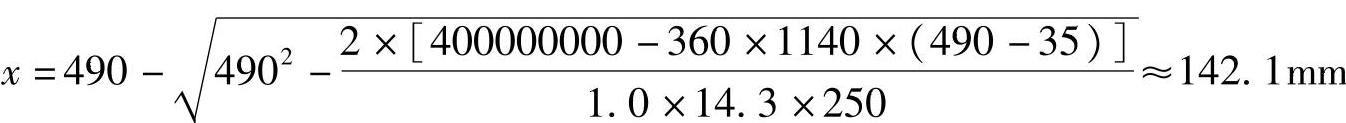
(2)验算压区高度x
根据《混规》式(6.2.10-3),2as′=2×35=70mm
根据《混规》式(6.2.10-4),ξbh0=0.518×490≈254mm
2as′=2×35=70mm<x=142.1mm≤ξbh0=0.518×490≈254mm
满足规范要求。
(3)求受拉钢筋As
由《混规》式(6.2.10-2),α1fcbx=fyAs-fy′As′,得:
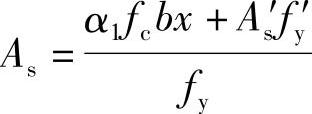
代入相关数据可得:
(4)配筋
受拉钢筋选3 25+3
25+3 22(As=1473+1140=2613mm2),截面配筋如图3.2.10所示。
22(As=1473+1140=2613mm2),截面配筋如图3.2.10所示。
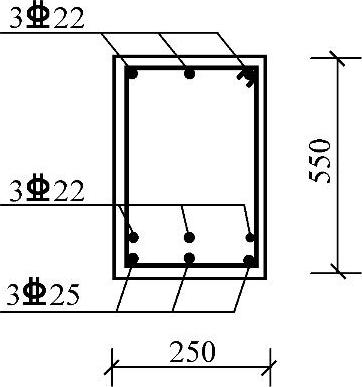
图 3.2.10
【例3.2.8】 双筋矩形截面梁的截面设计,As′已知,求As(ξ>ξb)
条件:已知条件同【例3.2.6】,但截面的受压区已配置受压钢筋2 14。
14。
要求:求所需的受拉钢筋As。
答案:确定基本数据
由《混规》附录A查得,As′=308mm2,其他同【例3.2.6】。
(1)求压区高度x
由《混规》式(6.2.12-1),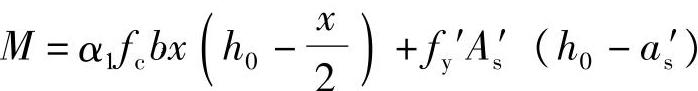 ,得:
,得:
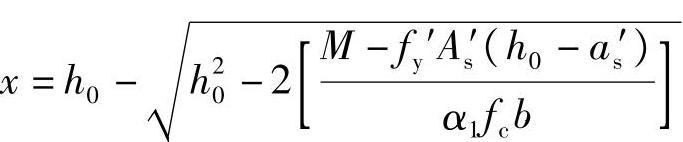
代入相关数据可得:
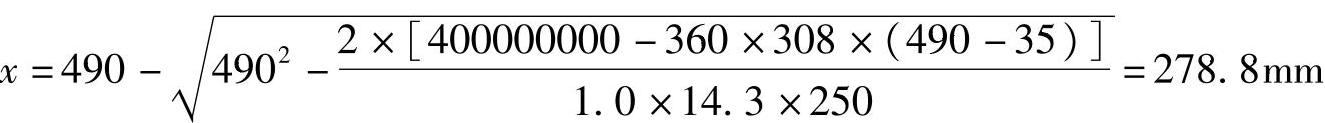
(2)验算压区高度x
根据《混规》式(6.2.10-3)、式(6.2.10-4)求解x,满足式(6.2.10-4)得:x=278.8mm>2as′=2×35=70mm
但不满足《混规》式(6.2.10-3):
x=278.8mm>ξbh0=0.518×490=254mm
说明原有配置的受压钢筋2 14太小,应按As′未知重新计算As′和As。
14太小,应按As′未知重新计算As′和As。
重新计算过程同【例3.2.6】
【例3.2.9】 双筋矩形截面梁的截面设计,As′已知,求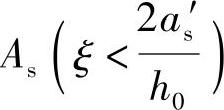
条件:已知条件同【例3.2.6】,但截面的受压区已配置受压钢筋4 25。
25。
要求:求所需的受拉钢筋As。
答案:确定基本数据
由《混规》附录A查得,As′=1964mm2,其他同【例3.2.6】。
(1)求压区高度x
由《混规》式(6.2.10-1),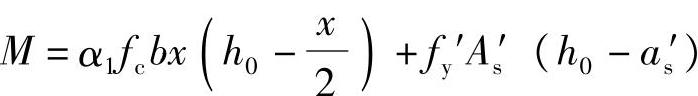 得:
得:
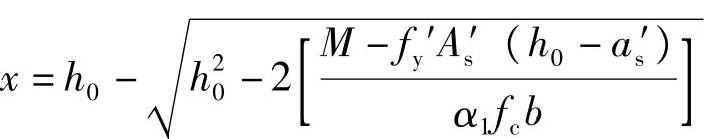
代入相关数据可得:
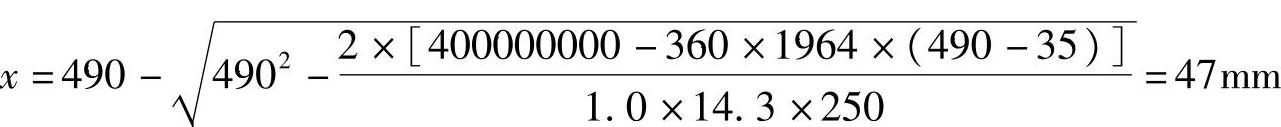
(2)验算压区高度x
根据《混规》式(6.2.10-3)、式(6.2.10-4)求解x,满足式(6.2.10-3)得:
x=47mm≤ξbh0=0.518×490=254mm
但不满足《混规》式(6.2.10-4):
x=47mm<2as′=2×35=70mm
(3)求受拉钢筋As
由《混规》式(6.2.14),M=fyAs(h0-as′),解得:
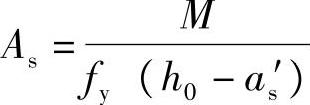
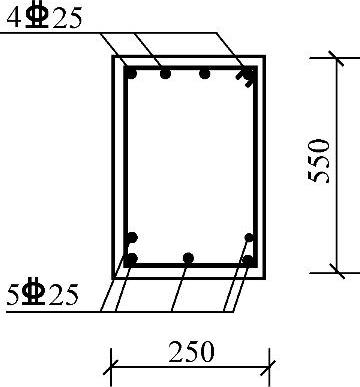
图 3.2.11
代入相关数据可得:
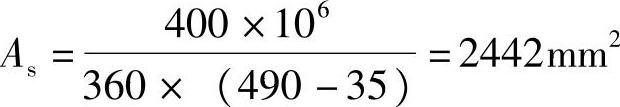
(4)配筋
受拉钢筋选5 25(As=2454mm2),截面配筋如图3.2.11所示。
25(As=2454mm2),截面配筋如图3.2.11所示。
(三)模拟考题
1.单筋梁
(1)承载力计算
【3.2.1】~【3.2.2】 某混凝土单筋矩形截面简支梁,截面尺寸和配筋如图3.2.12所示,采用C30混凝土,HRB400纵筋,安全等级为二级。
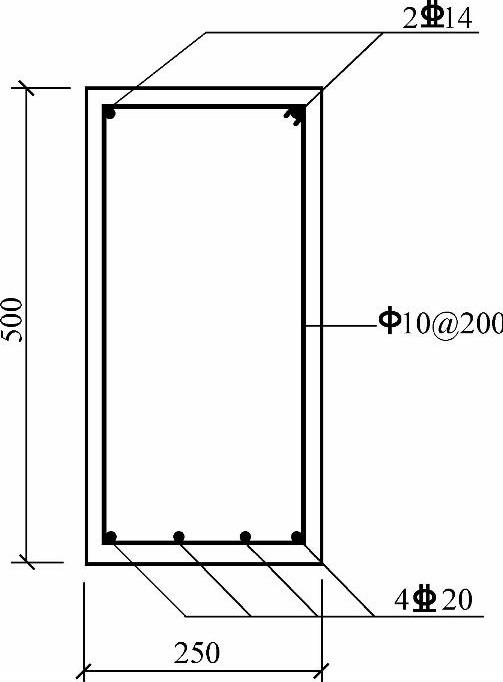
图 3.2.12
【3.2.1】 该梁能承受的弯矩设计值(kN·m)与下列何项数值最接近?(A)144.9 (B)148.3 (C)177.2 (D)158.3
正答:(C)
Ⅰ.详细解答
已知条件:b=250mm,h=500mm,fc=14.3N/mm2,ft=1.43N/mm2,fy=360N/mm2,ξb=0.518,As=1256mm2,取as=45mm,h0=500-45=455mm,α1=1.0。
①验算最小配筋率
根据《混规》第8.5.1条,ρmin取0.2%和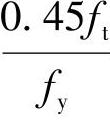 两者中的较大值,
两者中的较大值,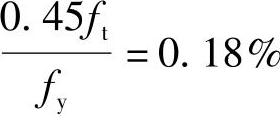 ,故取
,故取
ρmin=0.2%
Asmin=ρminbh=0.002×250×500=250mm2<As=1256mm2
②求压区高度x
由《混规》式(6.2.10-2)得:
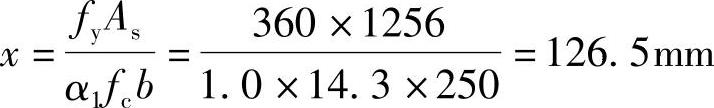
③验算压区高度x
根据《混规》式(6.2.10-3)得:
x=126.5mm<ξbh0=0.518×455=235.7mm,满足要求。
④求计算截面所能承担的弯矩设计值M
由《混规》第(6.2.10-1)条,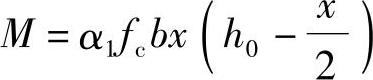
代入相关数据
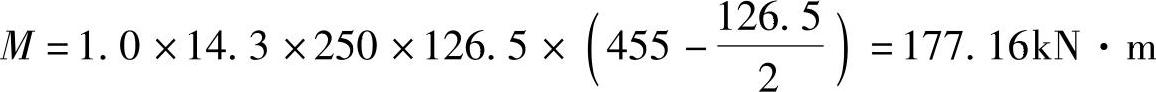
Ⅱ.简要解答(说明:因考试中的时间紧张,考生可按简要解答,其关键步骤不缺即可)
①ρmin=0.002和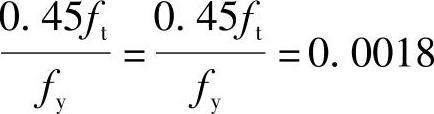 较大值,取ρmin=0.002
较大值,取ρmin=0.002
Asmin=ρminbh=0.002×250×500=250mm2<As=1256mm2,可以;
②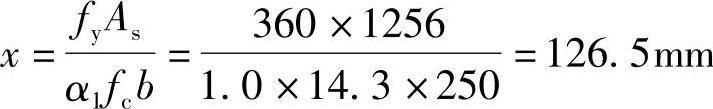 ;
;
③ξbh0=0.518×455=235.7>x=126.5mm,可以;
④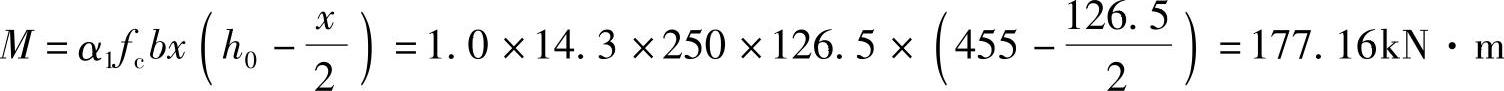 。
。
【3.2.2】 条件同上,若考虑架立筋2 14为受压钢筋,该梁承受的弯矩设计值需提高多少?(A)1% (B)3% (C)4.5% (D)7%
14为受压钢筋,该梁承受的弯矩设计值需提高多少?(A)1% (B)3% (C)4.5% (D)7%
正答:(C)
Ⅰ.详细解答
已知条件同【3.2.1】,As′=308mm2,as′=35mm
①求压区高度x,由《混规》式(6.2.10-2)得:
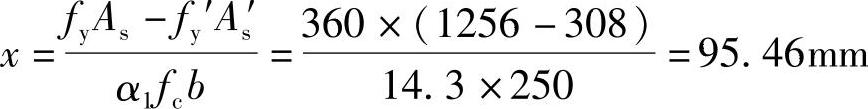
②验算压区高度x
根据《混规》式(6.2.10-3)、式(6.2.10-4):2as′=2×35=70mm<x=95.46mm<ξbh0=0.518×455=235.7mm
③确定受弯承载力M
由《混规》式(6.2.10-1):
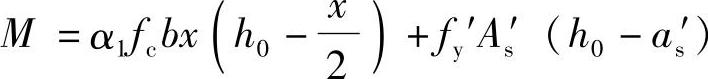
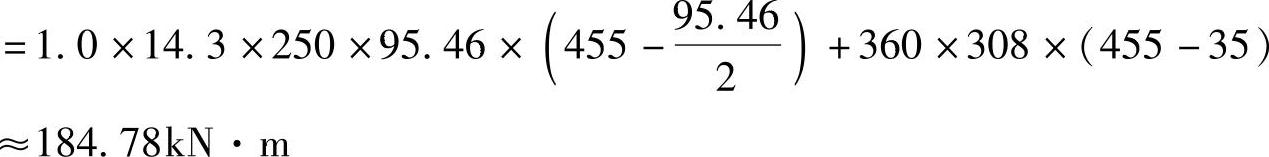
④弯矩设计值的提高百分率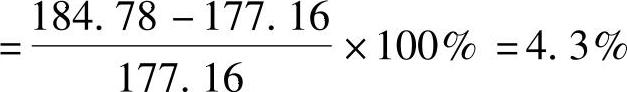
Ⅱ.简要解答

(2)配筋计算
【3.2.3】 某简支在砖墙的现浇钢筋混凝土平板(图3.2.13),板厚h=100mm,as=20mm。
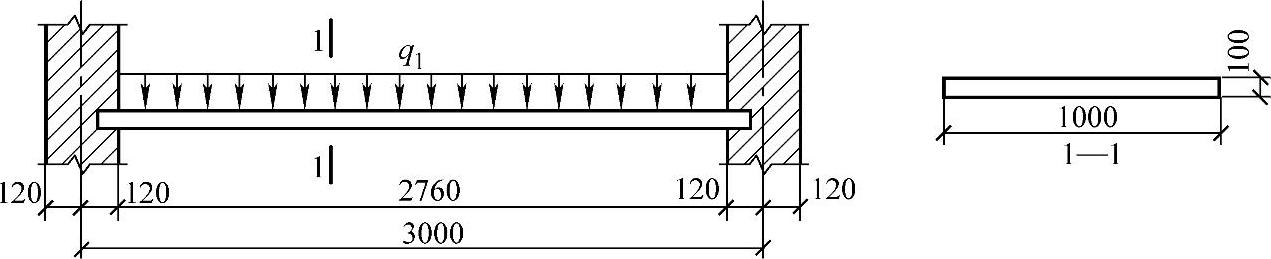
图 3.2.13
若混凝土强度等级采用C25,纵向受拉钢筋采用HRB335热轧钢筋。跨中最大弯矩设计值M=7.66kN·m,则As(mm2)与下列何项数值最为接近?
(A)190.5 (B)200.0 (C)337.2 (D)1745.3
正答:(C)
Ⅰ.详细解答
已知条件:b=1000mm,h=100mm,fc=11.9N/mm2,ft=1.27N/mm2,fy=300N/mm2,α1=1.0,ξb=0.55,h0=100-20=80mm,M=7.66kN·m
(1)求压区高度x
根据《混规》式(6.2.10-1),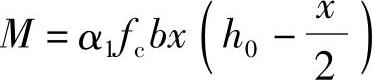 ,求得:
,求得:
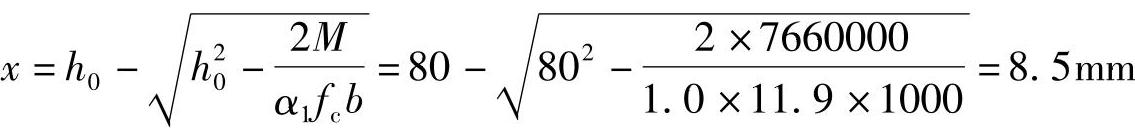
(2)验算压区高度x
根据《混规》式(6.2.10-3):x=8.5mm<ξbh0=0.55×80=44mm
(3)求受拉钢筋面积As
由规范式(6.2.10-2)α1fcbx=fyAs得:
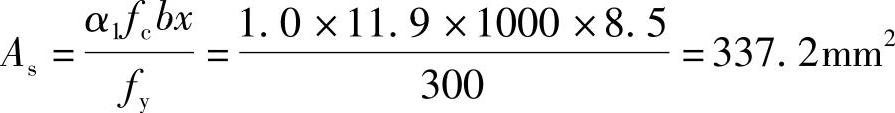
(4)验算受拉钢筋最小配筋率
由《混规》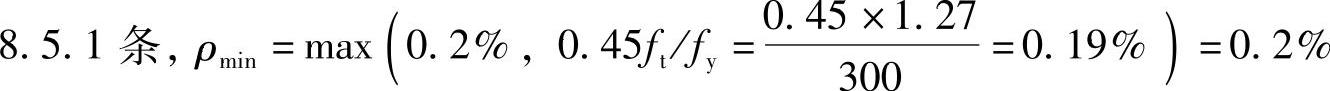
Ⅱ.简要解答

【3.2.4】 已知一单筋矩形截面梁尺寸为b×h=200mm×550mm,承受弯矩设计值M=238kN·m,采用HRB400级钢筋,混凝土强度等级为C30,则梁的纵向受力钢筋,以下何项配筋最为合适?
(提示:γ0=1.0,as=35mm)
(A)4 25 (B)3
25 (B)3 22(第一排)+2
22(第一排)+2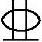 18(第二排)
18(第二排)
(C)5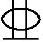 22 (D)3
22 (D)3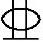 25(第一排)+2
25(第一排)+2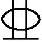 22(第二排)
22(第二排)
正答:(B)
Ⅰ.详细解答
已知条件:b=200mm,h=550mm,fc=14.3N/mm2,fy=360N/mm2,ft=1.43N/mm2,α1=1.0,as=35mm,h0=515mm,ξb=0.518,M=238×106kN·m。
(1)求压区高度x
由《混规》式(6.2.10-1)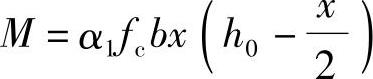 ,得:
,得:
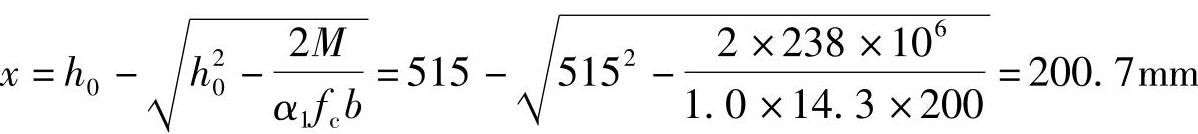
(2)验算压区高度x
由《混规》式(6.2.10-3)x<ξbh0,得:
x=200.7mm<ξbh0=0.518×515=266.77mm
(3)求受拉钢筋面积As
由《混规》式(6.2.10-2)α1fcbx=fyAs,得:
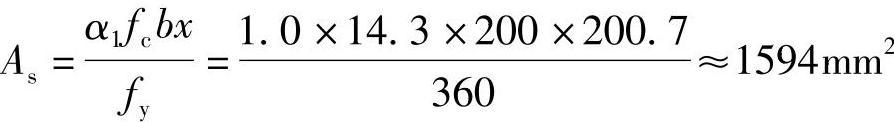
(4)验算As≥ρminbh
根据《混规》第8.5.1条,得
ρmin=min(0.2%,0.45ft/fy=0.18%)
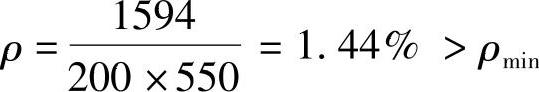 ,但b=200mm,一排钢筋摆放不下,改用二排,设as=60mm,h0=490mm,再重复以上步骤,得x=1736.6mm。
,但b=200mm,一排钢筋摆放不下,改用二排,设as=60mm,h0=490mm,再重复以上步骤,得x=1736.6mm。
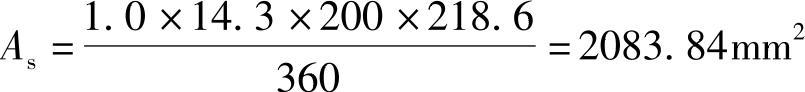
(5)配筋
选用3 25(一排)2
25(一排)2 18(第二排)As=1982mm2。
18(第二排)As=1982mm2。
Ⅱ.简要解答
因b=200mm一排钢筋摆放不下改用二排。
设as=60mm,h0=490mm,重新计算配筋,同上,略。
【3.2.5】 矩形截面梁尺寸b=250mm,h=550mm,采用C30级混凝土。如图3.2.14所示受拉区配有4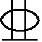 25+4
25+4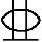 28纵向受力钢筋(HRB400级),则此梁的受弯承载力Mu(kN·m)最接近何项数值?
28纵向受力钢筋(HRB400级),则此梁的受弯承载力Mu(kN·m)最接近何项数值?
(A)588.4 (B)427.9
(C)380.61 (D)332.77
正答:(D)
Ⅰ.详细解答
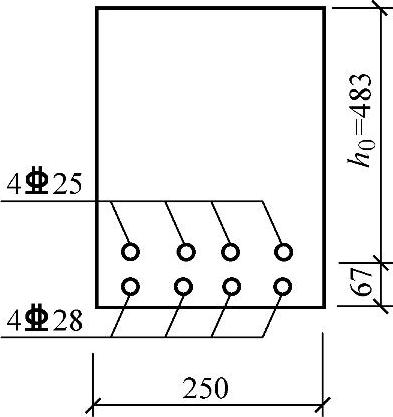
图 3.2.14
已知条件:b=250mm,h=550mm,fc=14.3N/mm2,ft=1.43N/mm2,fy=fy′=360N/mm2,as′=35mm,h0=483mm,As=4×(490.9+615.8)=4427mm2,ξb=0.518
(1)验算受拉钢筋最小配筋率
根据《混规》第8.5.1条As≥ρmin,因为本题图上已有双排钢筋,显然满足此条件。
(2)求压区高度x
由《混规》式(6.2.10-2)α1fcbx=fyAs,得:
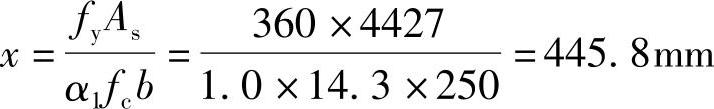
(3)验算压区高度x
根据《混规》式(6.2.10-3),得:
x=445.8mm>ξbh0=0.518×483=250.19mm
(4)确定受弯承载力
根据《混规》式(6.2.10-1),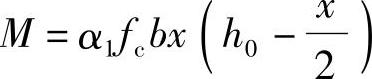
此时x=ξbh0,代入得M=α1fcbh20ξb(1-0.5ξb)
M=1.0×14.3×250×4832×0.518×(1-0.518/2)=320.12kN·m
Ⅱ.简要解答
(1)验算最小配筋率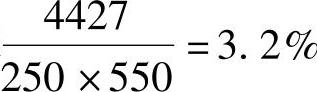 ,显然满足《混规》第8.5.1条。
,显然满足《混规》第8.5.1条。
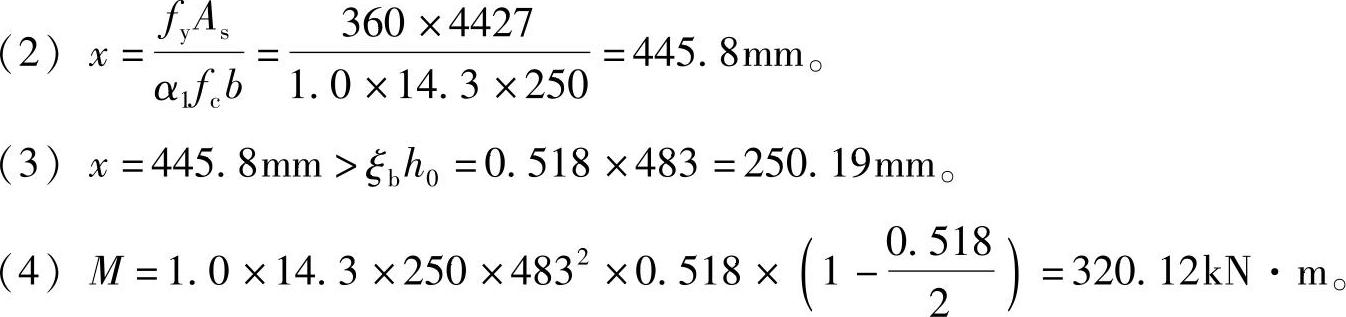
【3.2.6】 悬挑板的配筋(2010年,因规范改版,本题已作相应调整。)
某滨海海风环境风影区体育建筑中的钢筋混凝土悬挑板疏散外廊如图3.2.15所示。挑板及栏板建筑面层做法为双面抹灰各厚20mm。混凝土容重25kN/m3,抹灰容重20kN/m3。混凝土强度等级为C30,受力钢筋采用HRB335级( ),分布钢筋采 HPB300级(
),分布钢筋采 HPB300级( )。若该悬挑板按每延米宽计算的支座负弯矩设计值M=27kN·m,主筋采用
)。若该悬挑板按每延米宽计算的支座负弯矩设计值M=27kN·m,主筋采用 12钢筋,试问,当按单筋板计算时,该悬挑板的支座负弯矩钢筋配置,选用下列何项最为合适?
12钢筋,试问,当按单筋板计算时,该悬挑板的支座负弯矩钢筋配置,选用下列何项最为合适?
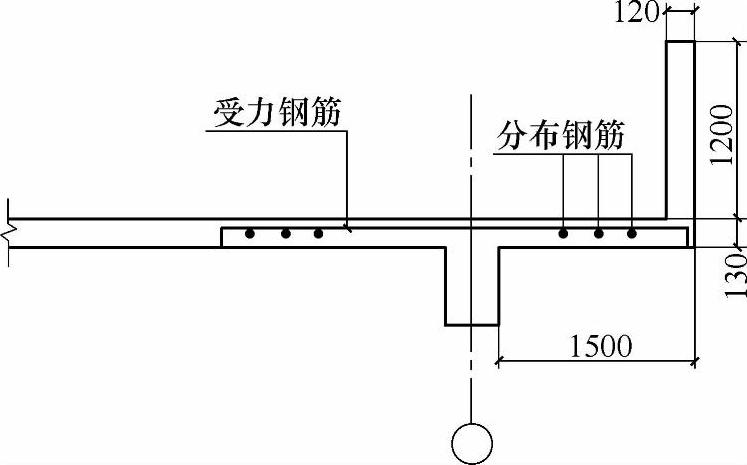
图 3.2.15
(A) 12@200 (B)
12@200 (B)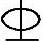 12@150 (C)
12@150 (C)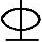 12@100 (D)
12@100 (D)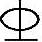 12@75
12@75
正答:(C)
详细解答
(1)《混规》表3.5.2,海风环境为三a类。
(2)《混规》表8.2.1,三a类环境,板保护层厚度30mm。
(3)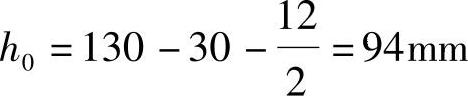 。
。
(4)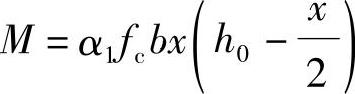
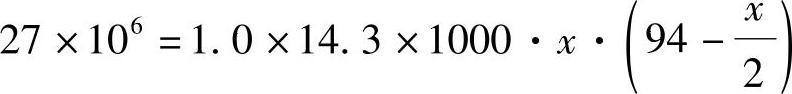
解得:x=22.9mm
(5)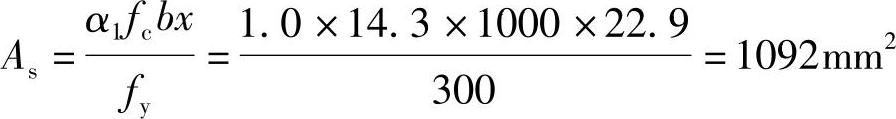 。
。
(6)《混规》表8.5.1,45ft/fy=45×1.43/300=0.21>0.20,取ρmin=0.21%。As,min=130×1000×0.21%=273mm2<1092mm2;
(7) 12@100,As=1130mm2>1092mm2,(C)正确。
12@100,As=1130mm2>1092mm2,(C)正确。
2.双筋梁
(1)承载力计算
【3.2.7】 已知双筋矩形截面梁的截面尺寸为b=250mm,h=500mm,as=as′=40mm,混凝土强度等级为C25,受拉钢筋为HRB400级,As=1140mm2(3 22),受压钢筋为HRB400级,As′=307.7mm2(2
22),受压钢筋为HRB400级,As′=307.7mm2(2 14)。则梁承受的最大弯矩Mu(kN·m)为何项数值?
14)。则梁承受的最大弯矩Mu(kN·m)为何项数值?
(A)251.0 (B)153.64 (C)169.2 (D)142.7
正答:(C)
Ⅰ.详细解答
已知条件:α1=1.0,fc=11.9N/mm2,fy=360N/mm2,fy′=360N/mm2,ξb=0.518,h0=h-as=500-40=460mm。
(1)计算混凝土受压区高度
由《混规》式(6.2.10-2):α1fcbh=fyAs-fy′As′
x=(fyAs-fy′As′)/α1fcb=(360×1140-360×307.7)/(1.0×11.9×250)=100.7mm
(2)验算压区高度
根据《混规》式(6.2.10-3)、式(6.2.10-4):
x<ξbh0=0.518×460=238.3mm
x=100.7mm>2as′=2×40=80mm
(3)计算该梁能承受的最大弯矩值Mu
由《混规》式(6.2.10-1):
Mu=α1fcbx(h0-x/2)+fy′As′(h0-as′)
=1.0×11.9×250×100.7×(460-100.7/2)+360×307.7×(460-40)
=169.2×106N·mm=169.2kN·m
Ⅱ.简要解答
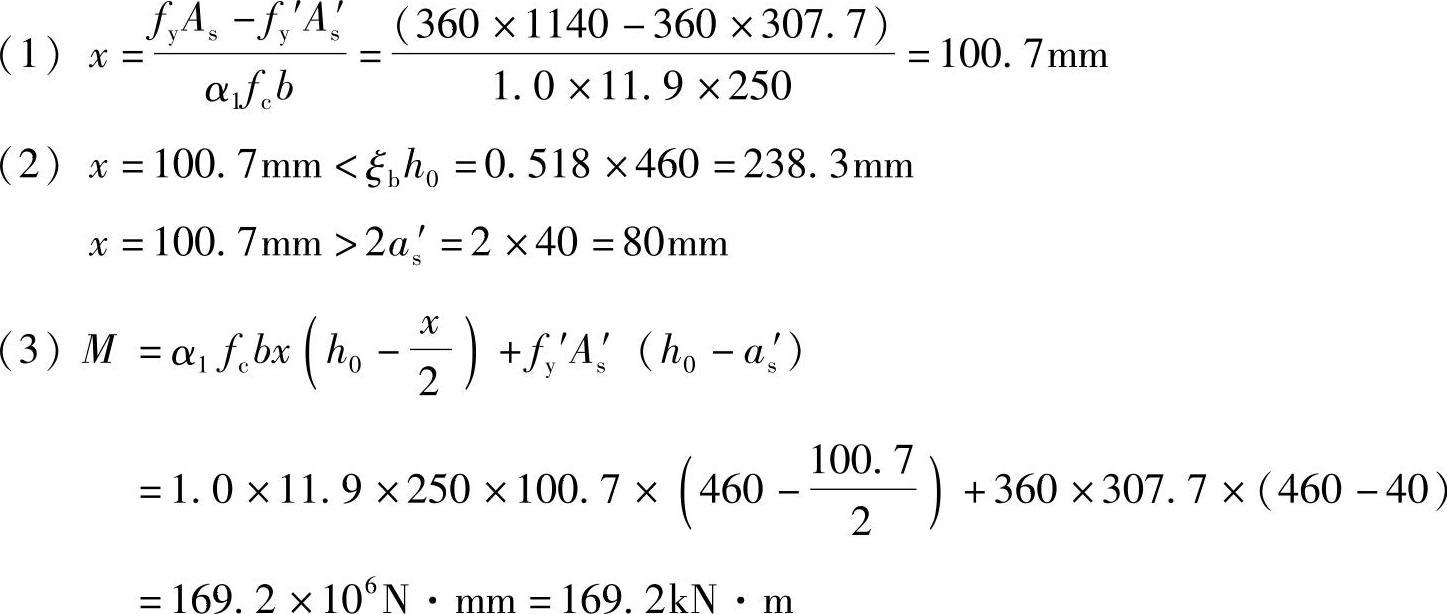
(2)配筋计算
【3.2.8】 梁的截面尺寸为b×h=250mm×500mm,C30混凝土,受拉钢筋HRB400级,受压钢筋用HRB400级,计算简图如图3.2.16所示,环境类别为一类。若Mmax=280.1kN·m,求梁的受拉配筋As(mm2)为何项数值?
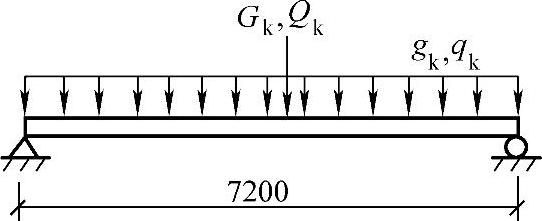
图 3.2.16
(A)2496.25 (B)2869.3 (C)2362 (D)2955.3
正答:(C)
Ⅰ.详细解答
已知条件:考虑弯矩较大,故受拉钢筋设计成双排,取as=60mm,h0=h-as=500-60=440mm,ξb=0.518,α1=1.0,fc=14.3N/mm2,fy=360N/mm2,fy′=360N/mm2,
(1)求压区高度x
直接由《混规》式(8.2.10-1),M≤α1fcbx(h0-x/2)
可以得到受压区高度x计算式:
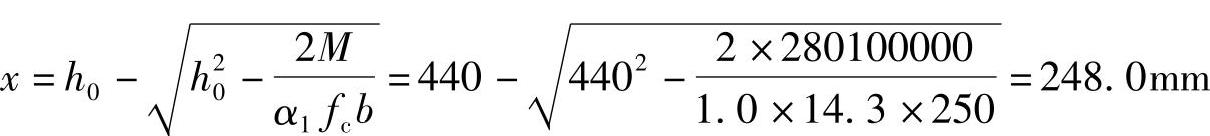
(2)验算压区高度x
由《混规》式(6.2.10-3):
x=248.0mm>ξbh0=0.518×440=227.9mm,超筋。
在不允许加大截面高度及混凝土强度等级的情况下,必须采用双筋截面,按双筋截面公式进行计算。
取as′=35mm
为使钢筋总用量最少,应充分利用混凝土抗压,令x=ξbh0=227.9mm。
(3)求受压钢筋As′
代入《混规》式(6.2.10-1),M≤a1fcbx(h0-x/2)+fy′As′(h0-as)
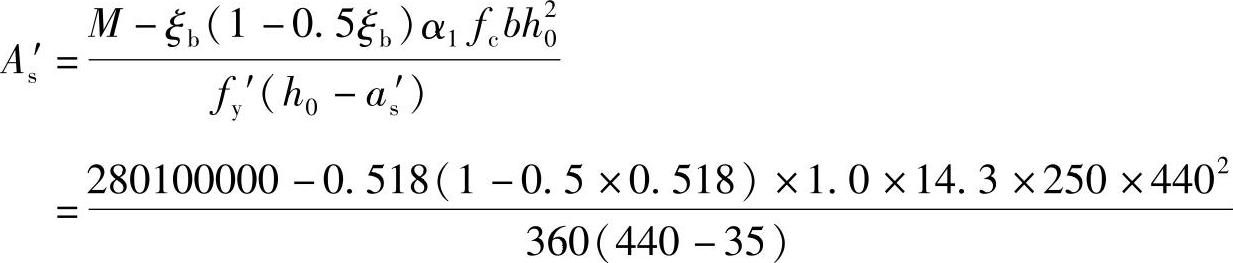
可得As′=99mm2
(4)求受拉钢筋
由《混规》式(6.2.10-2),可得α1fcbx=(fyAs-fy′As′),并取x=ξbh0可得:
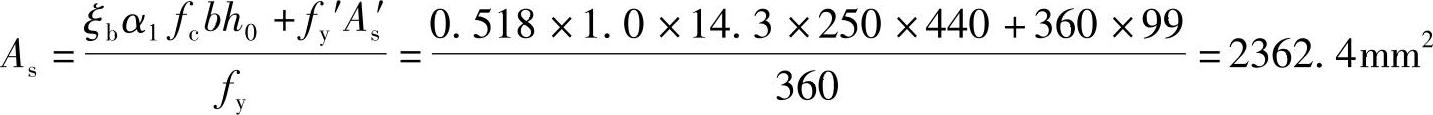
Ⅱ.简要解答
(1)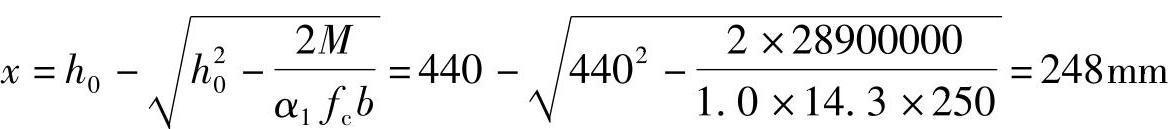
(2)x=248mm>ξhh0=0.518×440=227.9mm
(3)因截面不能改变,所以采用双筋梁。令x=ξbh0,求受压钢筋As′
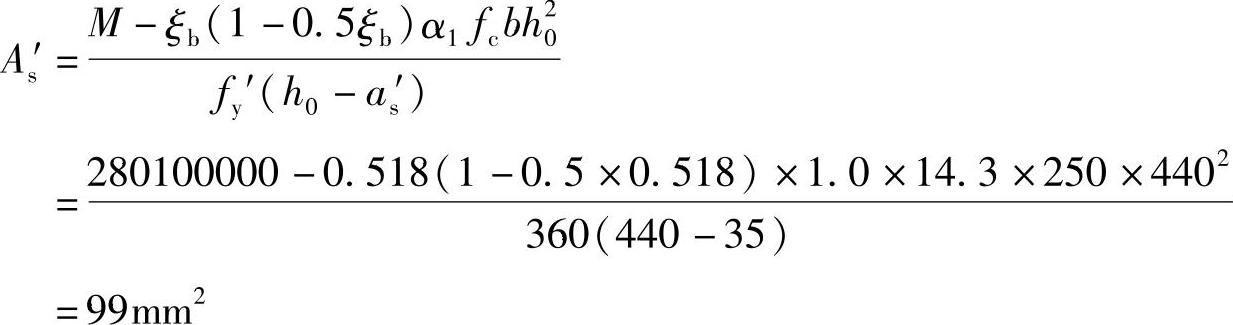
(4)求受拉钢筋As
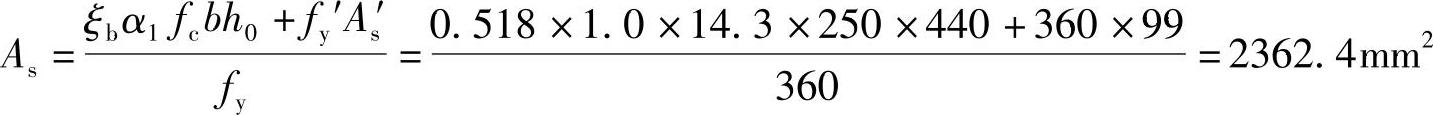
【3.2.9】 上题中,若已配置受压钢筋HRB400级3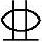 20(As′=941.0mm2),则As(mm2)最接近下述何项数值?
20(As′=941.0mm2),则As(mm2)最接近下述何项数值?
(A)1963 (B)2869.3 (C)2917.7 (D)2955.3
正答:(A)
Ⅰ.详细解答
已知条件同上,as′=35mm
(1)求压区高度x
将As′=941.0mm2代入《混规》式(6.2.10-1):
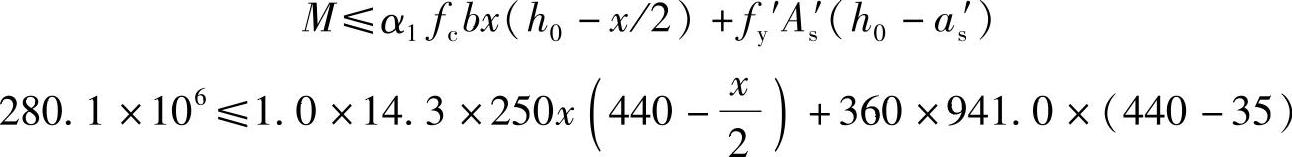
可得x=102.87mm。
(2)验算压区高度x,由《混规》式(6.2.10-3)、式(6.2.10-4):
x=102.87mm<xb=227.9mm且x>2as′=70mm,故受压钢筋配置是合适的。
(3)求受拉钢筋As
x=102.87mm,As′=941.0mm2,代入《混规》式(6.2.10-2):
α1fcbx=fyAs-fy′As′
即有1.0×14.3×250×102.87+941.0×360=360As
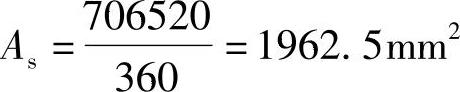
Ⅱ.简要解答
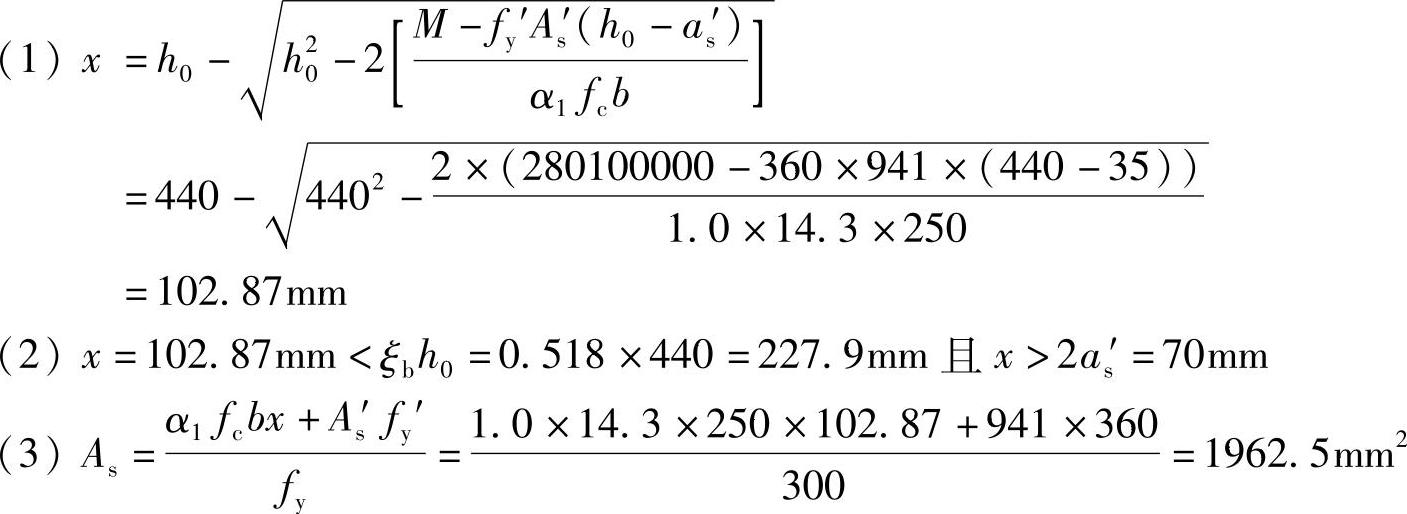
【3.2.10】 框架梁的受弯承载力(2011年)
假定,现浇框架梁KL1的截面尺寸为b×h=600mm×1200mm,混凝土强度等级C35,纵向受力钢筋采用HRB400级,梁端底面实配纵向受力钢筋面积As′=4418mm2,梁端顶面实配纵向受力钢筋面积As=7592mm2,h0=1120mm,as′=45mm,ξb=0.55。考虑受压区受力钢筋作用,梁端承受负弯矩的正截面抗震受弯承载力设计值M(kN·m)与下列何项数值最为接近?
(A)2300 (B)2700 (C)3200 (D)3900
正答:(D)
详细解答:
(1)Asfy=As′fy′+α1fcbx
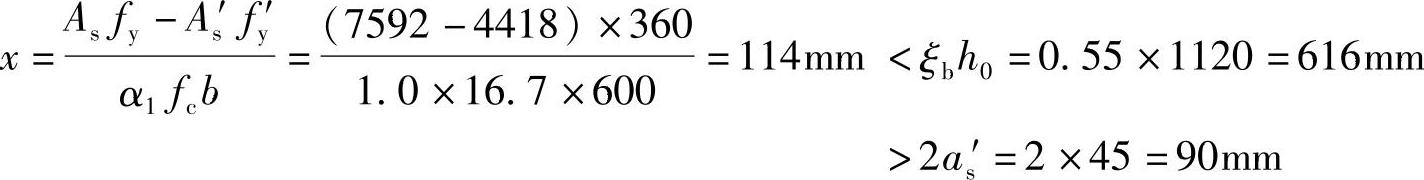
(2)查《混规》表11.1.6,受弯构件γRE=0.75
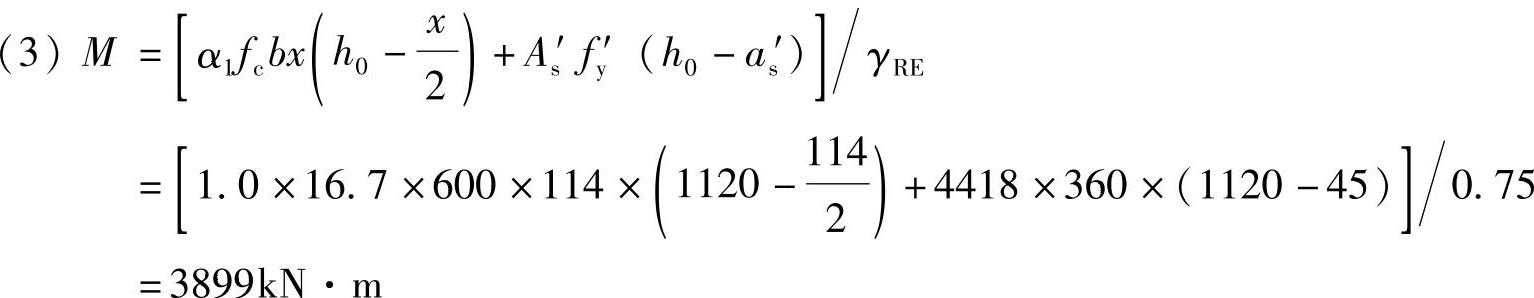
【3.2.11】 已知双筋矩形截面梁,截面尺寸为b×h=300mm×600mm,采用C25混凝土,纵向受力钢筋用HRB400级,跨中最大弯矩设计值M=254.9kN·m,梁的受压区已配置3 22纵向受压钢筋(As′=1140.4mm2),则梁的纵向受拉钢筋As(mm2)为何项数值?
22纵向受压钢筋(As′=1140.4mm2),则梁的纵向受拉钢筋As(mm2)为何项数值?
(提示:as=as′=35mm,γ0=1.0)
(A)1589.5 (B)1336 (C)3697.9 (D)4838.9
正答:(B)
Ⅰ.详细解答
已知条件:α1=1.0,fc=11.9N/mm2,b=300mm,h=600mm,as=as′=35mm,h0=565mm,As′=1140.4mm2,M=254.9×106N·mm
(1)计算截面混凝土受压区高度
将上述数值代入《混规》式(6.2.10-1):
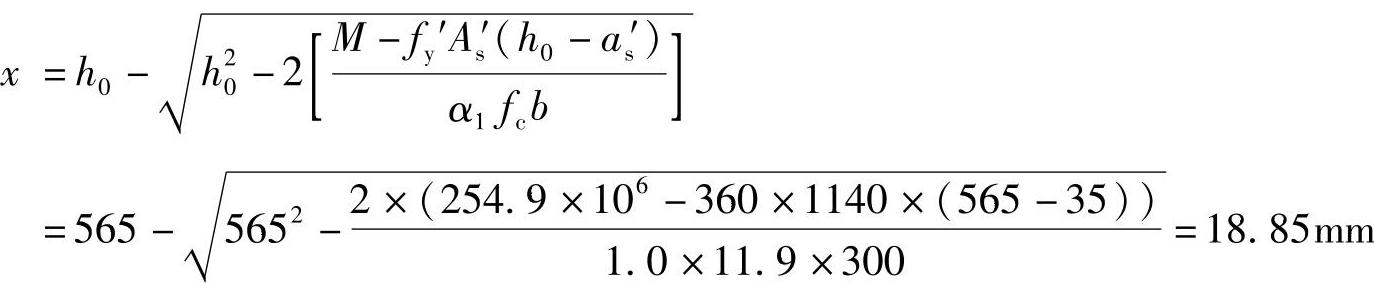
(2)验算压区高度x
根据《混规》式(6.2.10-4):
x=18.85mm<2as′=2×35=70mm
(3)求受拉钢筋As
由《混规》式(6.2.14),M=fyAs(h0-as′)
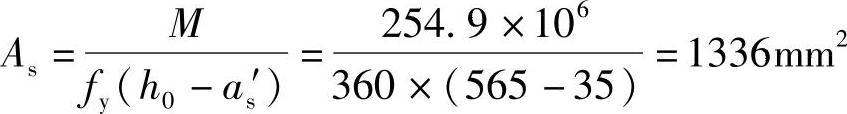
Ⅱ.简要解答