有孔板的受冲切承载力计算

二、有孔板的受冲切承载力计算

（一）考试要求

1.《考试大纲》的要求：掌握

2.“试题”回顾

【试题4.3.5】～【试题4.3.6】　（2007年）

某现浇钢筋混凝土楼板，板上有作用面积为400mm×500mm的局部荷载，并开有550mm×550mm的孔洞，平面位置示意如图437所示。

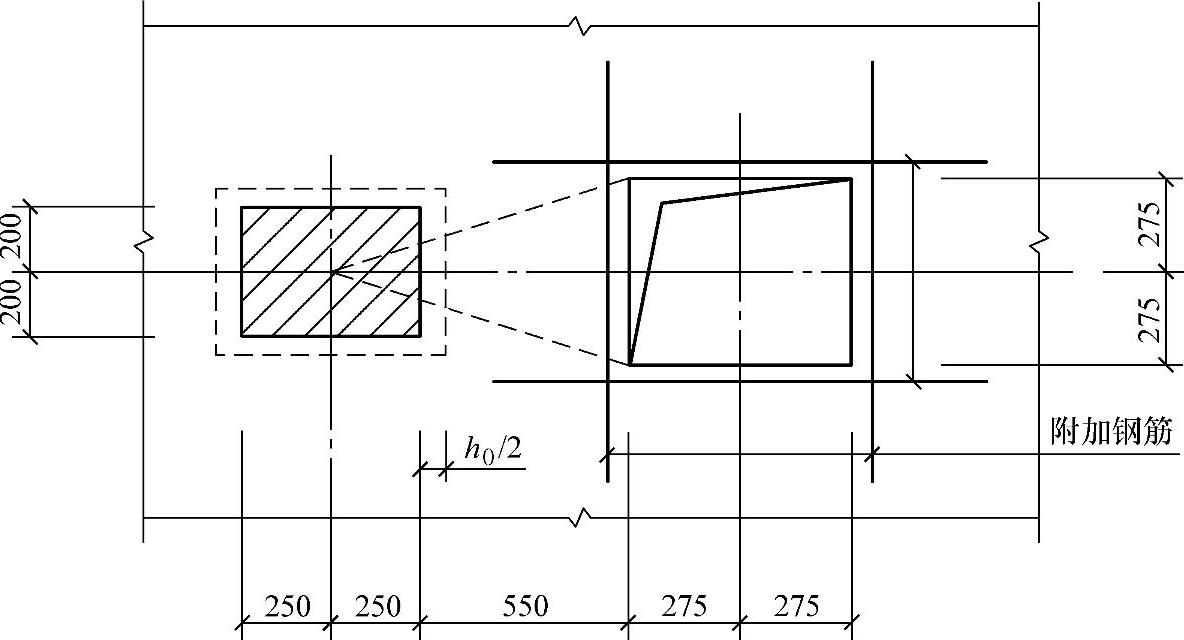
图　4.3.7

【试题4.3.5】　有孔板的受冲切承载力计算（2007年）

楼板混凝土强度等级为C25，板厚h=120mm，截面有效高度h₀=100mm。试问，在局部荷载作用下，该楼板的抗冲切承载力设计值[F_l]（kN），应与下列何项数值最为接近？

（A）177 （B）220 （C）272 （D）300

【试题4.3.6】　孔侧附加钢筋（2007年）

该楼板配置10@110的双向受力钢筋。试问，图4.3.7中孔洞边每侧附加钢筋的最低配置，应选用下列何项最为合适？

（A）2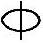12 （B）2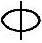14 （C）2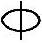16 （D）218

（二）《混凝土结构设计规范》规定

6.5.2　当板开有孔洞且孔洞至局部荷载或集中反力作用面积边缘的距离不大于6h₀时，受冲切承载力计算中取用的计算截面周长u_m，应扣除局部荷载或集中反力作用面积中心至开孔外边画出两条切线之间所包含的长度（图6.5.2）。

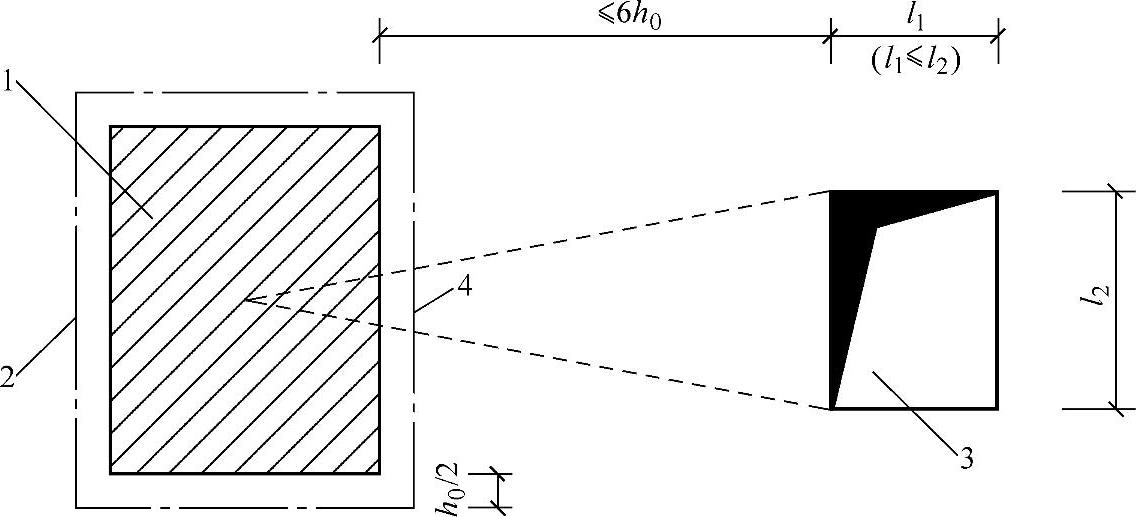
图6.5.2　邻近孔洞时的计算截面周长

1—局部荷载或集中反力作用面　2—计算截面周长　3—孔洞　4—应扣除的长度

注：当图中l₁大于l₂时，孔洞边长l₂用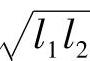代替。

（三）算例

【例4.3.3】　无梁楼板（有孔）的受冲切承载力计算

条件：已知一无梁楼板，柱网尺寸为55m×5.5m，板厚160mm，中柱截面尺寸为400mm×400mm；楼面荷载设计值（包括自重在内）为7kN/m²；混凝土为C30级（f_t=1.43N/mm²），在距柱边565mm处开有一700mm×500mm的孔洞，安全等级为二级，环境类别为一类（图4.3.8）。

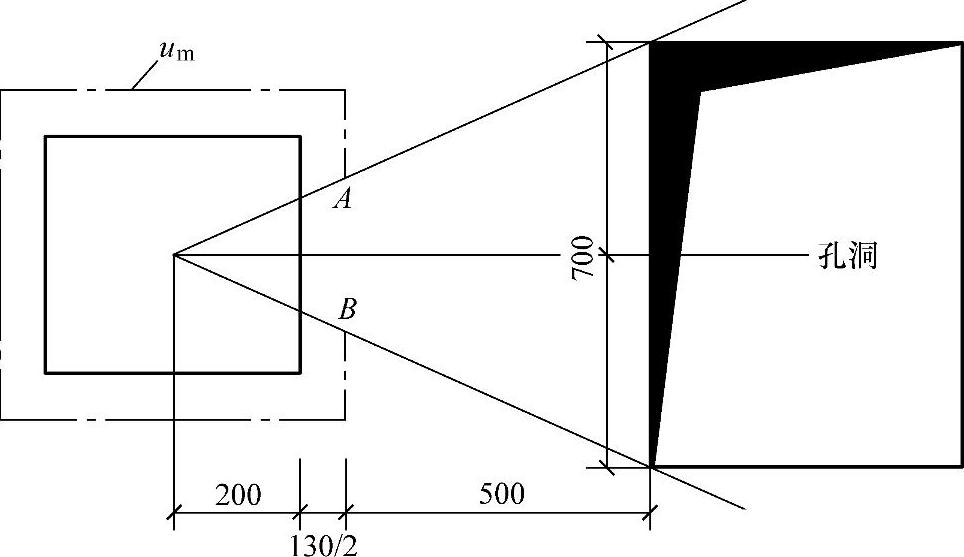
图　4.3.8

要求：试验算板的受冲切承载力是否安全。

答案：（1）查《混规》第8.2.1条知，混凝土保护层厚度为15mm，设纵向钢筋合力点到近边距离a_s=30mm，h₀=h-a_s=（160-30）mm=130mm。

（2）计算F_l

柱轴压力：N=7×5.5×5.5kN=211.75kN

冲切集中反力：

F_l=N-q（b+2h₀）2=211.75-7×（0.4+2×0.13）2=208.7kN

（3）求u_m，根据《混规》第6.5.1条的规定：

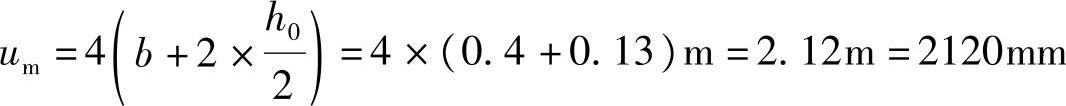
但板开有洞口因6h₀=6×130=780mm＞565mm，根据《混规》第6.5.2条的规定，尚应考虑开洞的影响。由图4.3.8知：

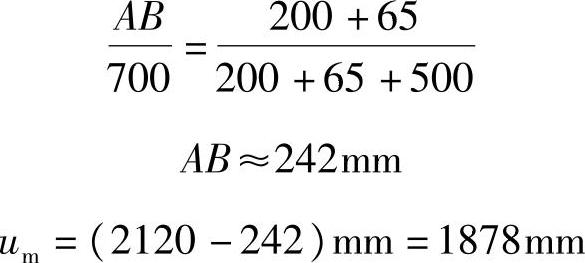
因集中反力作用面积为正方形，故取β_s=2，按《混规》式（6.5.1）得：

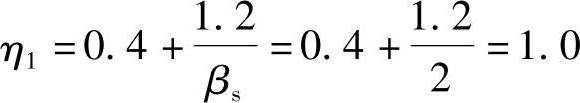
因该柱为中柱，故取a_s=40。

按《混规》式（6.5.1-3）得：

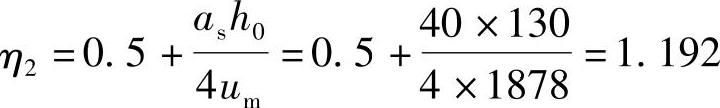
因η₁=10＜η₂=1.192，故取η=1.0。

（4）求冲切承载力

因板厚h=160mm＜800mm，根据《混规》第6.5.1条的规定，取β_h=1.0。

按《混规》式（6.5.1-1）得：

0.7β_cf_tηu_mh₀=0.7×1.0×1.43×1.0×1878×130N≈244380N≈244.4kN

＞2071kN，满足要求。

（四）模拟考题

【4.3.4】～【4.3.5】　已知一无梁楼板，柱网尺寸为5.5m×5.5m，板厚为160mm，中柱截面尺寸为400mm×400mm；混凝土强度等级为C30，在距柱边565mm处开有一700mm×500mm的孔洞，如图4.3.9所示，a_s=25mm。

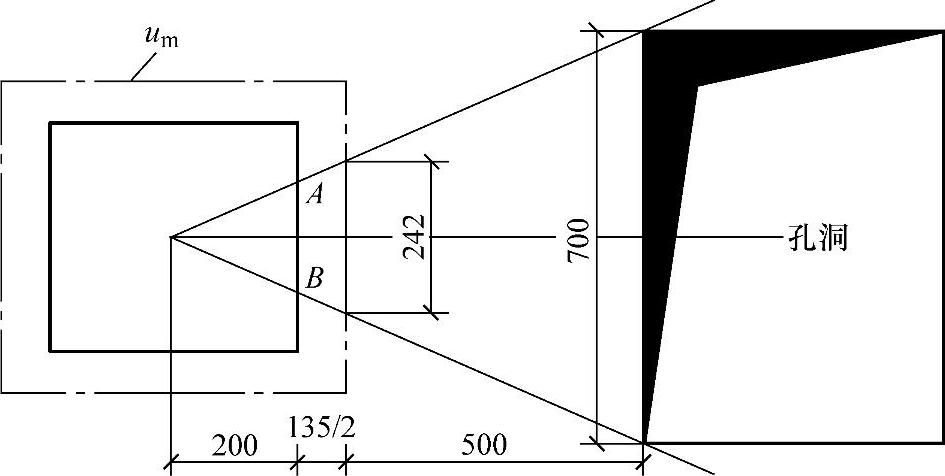
图　4.3.9

【4.3.4】　设板上承受均布荷载标准值为恒荷载q₁=15kN/m²（包括自重），活荷载q₂=5kN/m²，则无梁楼板承受的集中反力F_l（kN）与下列何项数值最为接近？

（A）745 （B）698 （C）845 （D）656

正答：（A）

h₀=h-a_s=（160-25）mm=135mm

楼板所受均布荷载设计值：q=（15×1.2+5×1.4）kN/m²=25kN/m²

柱子所受轴力：N=5.5×5.5×25kN=756.25kN

集中反力设计值：F_l=N-（b+2h₀）2×q=N-（0.4+2×0.135）2×25=745.03kN

【4.3.5】　假设AB的长度之和为242mm，若该楼板不配置抗冲切钢筋，楼板的受冲切承载力设计值（kN）与下列何项数值最为接近。

（A）256.5 （B）338.8 （C）423 （D）321.5

正答：（A）

根据《混规》第6.5.1条的规定：

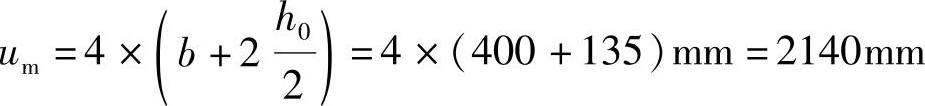
因为：6h₀=6×135mm=810mm＞565mm

根据《混规》第6.5.2条的规定，应考虑开洞的影响，因此临界截面周长：

u_m=（2140-242）mm=1898mm

按《混规》第6.5.1条规定：

因柱的截面尺寸为正方形，故β_s=2，；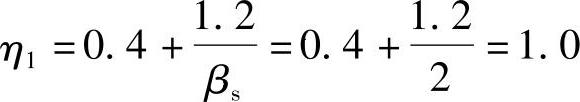

因柱为中柱，故α_s=40，由《混规》式（6.5.1-3）可知：

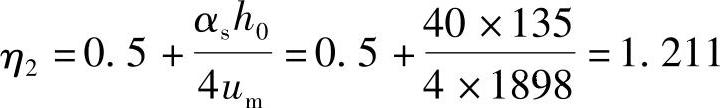
因η₁＜η₂，故取η=η₁=1.0，所以有

0.7β_hf_tηu_mh₀=0.7×1.0×1.43×1.0×1898×135N≈256500N=256.5kN。