“妖魔曲线”

能不能用一系列已知图形来“生成”一个未知的极限图形呢？在这里，我们把“逼近”改成了“生成”，其区别在于：当阿基米德等人和刘徽用一系列正多边形来“逼近”圆的时候，圆已经在他们心目中存在了，也就是说，圆是什么样子的，它有些什么基本性质，这些都已经很明确了；而现在，我们要“生成”的极限图形，它是什么样子的，它有些什么基本性质，我们都不知道。

这个想法是不是也很自然呢？这很难说，因为在长达2000多年的时间中，没有人想到用这个方法来生成未知的图形。然而，到19世纪，首先是德国数学家维尔斯特拉斯发现了一条“妖魔曲线”，这条曲线上的每一点都是“转折点”，也就是说，它在每一点都像多边形的边在其顶点处那样发生转折。这真有点儿让人不可思议。接着，意大利数学家皮亚诺发现了一条能填满一个正方形的也是处处为“转折点”的“妖魔曲线”。这两种“妖魔曲线”原则上都是用上述方法“生成”的。

到本世纪初，这种“妖魔曲线”大量出现。其中比较典型的是1904年由瑞典数学家科克发现的雪花曲线。

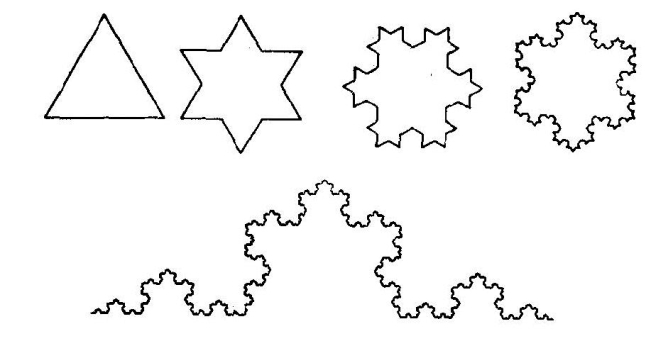
科克雪花曲线

科克的雪花曲线是从一个简单的正三角形开始生成的。首先以这个三角形每条边中间三分之一的那条线段为底边，向外作一个小正三角形，然后抹去小正三角形的底边，这样，就生成了一个六角形。以后对每次生成的图形都作如此处理（即在图形的每条边上都向外作一个小正三角形，并抹去它的底边），以至无穷。于是，一条奇妙的雪花曲线便生成了。

科克雪花曲线有一些出人意料的性质。它是一条处处是“转折点”的曲线，它的长度为无穷大，但它围成的面积却是一个有限的数值——最初那个正三角形的8/5。更重要的是，这种曲线虽然十分复杂，我们根本不可能把它画出来（我们在图中所表示的仅是它生成过程中开头的几个图形），但它的任何一段都是相似的。也就是说，如果用一个放大镜去“看”它的一段曲线的话，不管这个放大镜的放大倍数是多少，我们“看”出来的曲线形状都是一样的。这个重要的特点称为“自相似”。“自相似”说明这种曲线是不分层次的，即在任何一个层次上，这种曲线都是一样的。

谢尔宾斯基“垫片”

除了科克雪花曲线这类“妖魔曲线”外，本世纪初还出现了“妖魔”平面形和“妖魔”立体形，最著名的要数俄国数学家谢尔宾斯基给出的谢尔宾斯基“垫片”、谢尔宾斯基“地毯”和谢尔宾斯基“海绵”。一时间，“群魔乱舞”，令数学家大伤脑筋。

谢尔宾斯基“地毯”