分形与非线性
非线性科学一瞥
蝴蝶效应
洛伦兹教授的计算机
1961年冬季的一天,美国麻省理工学院的洛伦兹教授正在他那台计算机上做着模拟天气预报的实验。这是一台老掉牙的计算机,它由一大堆真空电子管组成,笨拙丑陋,占据着办公室的一角,运转时发出令人心烦的噪声。
严格地说,洛伦兹教授是一位数学家,而不是一位气象学家。1938年他大学毕业时,就认为数学是自己的终生职业。然而第二次世界大战改变了一切,他成了美国空军的一名气象预报员。战后他决定留在气象界,因为他迷上了气象预报工作。
是的,世界上还有什么能比预言未来更吸引人呢?科学的魅力之一就在于:科学能预言未来!如果说古代的星象家能准确地预报日食、月食的发生,因而倍受人们尊崇的话,那么近代科学家对彗星回归日期的精确计算、对冥王星的准确猜测,以及近年科学家对太空事件(例如1994年的“彗木亲吻”)的正确预言等等,更是令人叹为观止。
在现代社会中,气象预报是一件极其重要的工作,当过空军气象预报员的洛伦兹比别人更清楚这一点。1944年6月,伟大的诺曼底登陆战前夕,当盟军最高司令艾森豪威尔听完了一位气象军官的汇报后,仅仅问了一句:“有把握吗?”顿时,这位气象军官感到:全人类的命运都维系在他的回答上了!
一切事物的变化都是可以预报的吗
由17世纪伟大的英国科学家牛顿所开创的近代自然科学体系,使人们树立了这样一个观念:世界上一切事物的变化不但是有规律的,而且这些规律都可以用数学方程式表达出来。我们只要知道了事物目前的状态,就可以通过这种数学方程式计算出事物未来的状态。就好比我们常做的那种数学应用题:“甲乙两地相距××千米,现有两列火车分别从两地相向开出,甲火车每小时行××千米,乙火车每小时行××千米……”根据这些条件,我们就可以列出方程式,计算出这两列火车何时相距多少千米,何时相遇,等等。现在世界上之所以还有许多事物的未来状态我们不能预知,或者是因为这种事物的目前状态还不能完全被测知,或者是因为表达这种事物变化规律的数学方程式还没有研究出来,或者是因为通过有关数学方程式所进行的计算过于复杂,人们无法在有效的时间内把结果计算出来。
当1961年冬天,我们的洛伦兹教授进行着模拟气象预报的实验的时候,他就是这种观念的信奉者。
“制造”天气
本世纪60年代,气象预报还是一项经验性的工作。气象预报员测风观云,然后根据经验猜测明天的天气情况。显然,这样的预报,特别是中长期的天气预报,是远不能令人满意的。既受过数学专业教育又是气象工作者的洛伦兹决心在这方面有所作为。他想先做一些模拟气象预报的实验。
气象,实际上就是地球大气圈底层中的各种与大气运动有关的物理现象,如气温、气压的变化等。而关于大气运动的规律,科学家们早已总结出了一些数学方程式。作为一种模拟实验,洛伦兹选择了一组较精简的方程。为预报未来气象而必需的目前气象状况,应该由遍布全球的气象观测站提供。现在是做实验,可以自己假设。至于计算,就只能依靠那台老爷计算机了。
于是,一个由洛伦兹人为“制造”的“天气”在那台计算机上按部就班地开始表现出各种气候现象:今天刮南风,气温在28摄氏度,明天刮北风,气温20摄氏度……,如此等等。根据上面所说的那种观念,未来任何时候的天气情况,都可以由计算机准确地计算出来,只要计算机不出毛病,而且你也有足够的耐心。
这天,洛伦兹教授想检验一下计算结果是否可靠,他采取的方法是把已经计算过的数据再计算一遍,看看两次结果是否相同。但是,他玩了个小花样,他不是从上次计算时最初输入的数据开始验算,而是把上次计算过程中的一个中间结果作为这次验算的输入数据。洛伦兹想,这没有什么关系,这至少可以检验一下计算过程后半段的可靠性。为了躲避计算机那令人心烦的噪声,他离开办公室,到餐厅去喝一杯咖啡。
大相径庭
一个小时之后,他回到办公室,一件意想不到的事正等待着他:这次计算结果本来应该完全重复上次的计算结果,但是现在这两个结果却大相径庭,就好比是一个预报几个月后的某天是晴空万里,另一个却预报这一天是电闪雷鸣,简直是驴头不对马嘴。洛伦兹的第一个念头是:又坏了一只真空管。
说也奇怪,就在这时,一种突然间的灵感使洛伦兹领悟到:计算机没有毛病,问题出在他输入的数据上。原来,这台计算机在计算时,对每个数据都保持着6位数字的精确性,例如0.506127。但是在输出打印时,为了节省地位,只打印经过四舍五入的前3位,例如0.506。洛伦兹在将上次计算的中间结果输入时,就是只输入这前3位。他认为如此省略是合理的。确实,千分之一的误差实在算不了什么。如果气象预报能达到这样的精确度,那完全可称得上无可挑剔了。然而,恰恰是这千分之一的误差,导致了可说是灾难性的后果。这正应了中国的一句老古话:“差之毫厘,失之千里。”
桀骜不驯的非线性方程
洛伦兹仔细地观察了他的这两种“模拟天气”是怎样分道扬镳的,他要弄清楚到底是什么原因使他的“模拟天气”居然容不得这区区误差。计算程序是不会有什么问题的,何况两次计算用的是同一个计算程序。计算机虽老,但是看来还是忠心耿耿地执行着它的任务。如此说来,原因难道在他所选择的那一组方程式上?
确实是这样。这些方程式本身是没有什么问题的,它们确实表达了大气运动的规律。但是,描写事物变化规律的方程式分为两类,一类称为线性方程,一类称为非线性方程。线性方程所代表的变化过程比较平滑,看上去很有规则,对外界的抗干扰能力也较强,一般的省略和误差都不会给它们带来较大的影响。而非线性方程所代表的过程则显得有点桀骜不驯,看上去没有规则,对外界的一些十分微小的干扰也表现出激烈的变化。长期以来,科学家研究的主要是线性方程,因为它们比较容易对付,而且用线性方程所作的预测基本上都取得了成功。而对于非线性方程,人们则敬而远之,因为找不到一种普遍的方法来解决它们。然而正是非线性方程,描写了自然界中的绝大多数现象,比如旋涡、湍流、地震等等。洛伦兹选择的那一组方程就是非线性方程,而且描写大气运动的方程都是非线性方程。看来真是“厄运难逃”,长期的天气预报注定不能成功,因为这些非线性方程不能容忍哪怕一丁点儿的误差,而完全没有误差是不可能的!

混沌学的序曲
对于这种微小干扰能引起巨大变化的现象,洛伦兹作了一个生动的比喻:一只蝴蝶在巴西扇动一下翅膀,会在美国的得克萨斯州引起一场龙卷风。后来人们就把这种现象称为“蝴蝶效应”
由于非线性方程所描写的过程看上去混乱、无序、没有规则,西方的科学家就用一个意思为“混乱”的词chaos来称呼这种过程,中国的科学家则从中国古代哲学家的著作中取出“混沌”一词、作为这种过程的名称。研究混沌过程的学科就叫做“混沌学”,这门新学科就是以洛伦兹的意外发现为萌芽的。
混沌过程似乎杂乱无章,无法预测,但从总体上看还是有规律的。就好比长期天气预报注定要失败,但是天气的一年四季变化规律,却是井然有序、亘古不变的。
探索混沌过程的变化规律,就是混沌学的任务。混沌学是非线性科学的一个重要部分,它的研究还刚刚开始,还有许许多多的奥秘等待着人们去揭开。
非线性方程
这里所指的方程一般是微分方程。与我们在中学里学的方程不同的是,微分方程中要解出的不是未知数,而是未知函数,而且在微分方程中,不但有可能出现未知函数及其自变量,而且一定会出现未知函数的微商。所谓微商,可以理解为函数的变化率。例如速度是位移随时间的变化率,所以速度函数是位移函数的微商(均以时间为自变量);又如加速度是速度随时间的变化率,所以加速度函数是速度函数的微商(也均是以时间为自变量)。如果微分方程中出现的未知函数和它的微商都是一次的,则这个方程称为线性微分方程,有时简称为线性方程。否则,就称为非线性微分方程或非线性方程。
孤立子传奇
他看见一“堆”水在前进
1834年的一天,年轻的英国造船工程师斯科特·罗素正在爱丁堡郊外对一条运河进行河道勘察。这条运河是连接爱丁堡与格拉斯哥这两个著名英国城市的,河上不时有船只通过。那天天气晴朗,罗素心情也十分好,他工作了一会儿,便直起身来眺望河上那迷人的景色。
这时,从远处驶来一条船,这船所用的“动力”用今天的眼光来看真有点儿特别,那是在岸边奔跑着的两匹马。只见船儿被两匹马拉着在狭窄的河道中快速前进,船头激起阵阵浪花,给人以一种一往无前的感觉。不知什么缘故,船突然停下了。就在这一刻,罗素看到了后来使他永垂史册的奇妙景象:
本来在船体周围被船体带着前进的水流,这时聚集到了船头,并处于急剧运动状态,接着就形成一个光滑、轮廓分明的巨大水峰,以较快的速度离开船头向前移动。这水峰大约长30英尺(1英尺约合0.305米),高1~1.5英尺,行进的速度约每小时8~9英里(1英里约合1.609千米)。
良好的科学素质往往表现为对大自然新奇现象的穷追不舍,这会儿,罗素真的是“穷追不舍”了。他来不及仔细考虑,立即翻身上马,紧紧跟随而去。只见那水峰在行进过程中,高度渐渐减小,走了一二英里后,终于消失在蜿蜒曲折的河道之中。
后来,罗素描写道:“这绝不是被分离的通常的波,因为通常的波在前进时,总是一部分高于水面,一部分低于水面。不仅如此,它的形状也与通常的波不同。它也不是半个波,而是一个完整的波。这个波不是一部分在水面上,一部分在水面下,而是始终在水面之上。除此之外,这‘堆’水也不是停留在一个地方,而是前进了相当一段距离。”

罗素把他的发现称为“伟大的孤立波”,并用了毕生的精力来进行这方面的实验和研究。罗素认为,这种“孤立波”应当表现为流体力学中有关方程的一个解,然而,由于当时数学水平的限制,他始终不能给这种现象以理论上的圆满解释,他的观点也不能得到当时英国科学界的认可。因此,罗素热忱地希望“将来的数学家”能完成这项工作。
打入“冷宫”
光阴荏苒,时间过了约60年。到1895年,有两位数学家,一位叫科特维格,一位叫德弗里斯,在研究单方向运动的浅水波时,建立了一个非线性方程,人们用科特维格和德弗里斯的姓氏词头缩写来命名这个方程,称之为KdV方程。KdV方程有一类解,它们的基本形式是双曲正割函数的平方。如果把它们的函数图象画出来,形状就像我们在寺院里常看到的大钟那样,中间隆起,两旁向下伸展并逐渐趋于平坦。真是“踏破铁鞋无觅处,得来全不费功夫”,这正是罗素所发现的孤立波的数学表示。
KdV方程是一个非线性方程,非线性方程的一个特点是:它的解一般不能“叠加”。那么,什么叫做“叠加”?
我们在《蝴蝶效应》里已经介绍过,描写大自然变化过程的方程一般是微分方程。微分方程的解不是“数”,而是“函数”。微分方程一般可分为两类,一类是线性方程,一类是非线性方程。(https://www.daowen.com)
一般来说,线性方程在形式上包括两个部分:一部分包含着要求解的未知函数,它代表着某种自然规律;另一部分则不包含未知函数,它代表着外界作用。线性方程有一个很讨人喜欢的特点:如果f1(t)是一个线性方程的一个解,它代表着在某种自然规律支配下受到一定外界作用后所发生的变化过程,而f2(t)是类似线性方程(这个方程仅在代表外界作用的部分与前一方程有所不同)的一个解,它代表着在同一自然规律支配下受到另一外界作用后所发生的变化过程,那么f1(t)+f2(t)就代表着在这种自然规律支配下同时受到上述两种外界作用后的变化过程,也就是说,它是这样一个线性方程的解:这个方程在代表自然规律的部分与前两个方程完全相同,而其代表外界作用的部分则是前两个方程相应部分的和。人们把这个特点说成:线性方程的解是可以“叠加”的。这个特点在现实的自然界变化过程中的表现是:某种自然规律支配下的一个变化过程和同一规律支配下的另一变化过程相遇时,它们互不干扰,相互独立。
与线性方程相比,非线性方程就有点令人棘手了,因为它的解一般没有这样的“叠加”性质。孤立波是非线性方程——KdV方程的解,因此人们推测,当两个孤立波相遇时,它们将相互影响,导致波形被破坏殆尽。这样的孤立波是不稳定的,它对描述自然现象没有多大帮助,于是,虽然孤立波的数学表示被找到了,但孤立波仍被人们打入了“冷宫”。
被“解禁”的孤立子
历史在前进着,科学在发展着。不觉到了1965年,被“幽禁”了大半个世纪的孤立波有点耐不住寂寞,想出来看看世界变得怎么样了。不过它这次不是出现在爱丁堡附近的运河上,而是出现在20世纪的最伟大发明——电子计算机上。
本世纪60年代,电子计算机用在科学研究上已不是什么新鲜事了。这天,美国贝尔公司的两位科学家,一位叫克鲁斯卡尔,一位叫扎布斯基,正在用电子计算机对KdV方程进行数值计算。同预料的那样,他们得到了KdV方程的孤立波解,但是,令人意外的是,当两个这样的孤立波发生“碰撞”时,它们并没有相互造成“伤害”,居然都能保持各自的波形和速度不变。
这一发现引起了人们浓厚的兴趣,并使人们联想到微观世界中的粒子。于是,这种即使发生“碰撞”也保持自己形状和速度的孤立波就被称为“孤立子”,现在一般简称为“孤子”。
人们不久就发现,不但KdV方程有孤立子解,而且许多在应用中十分重要的非线性方程都具有孤立子解。这个事实说明,孤立子是自然界的一种相当普遍的非线性现象。于是,孤立子的研究很快就成为非线性科学的一个重要领域。
“负负得正”
那么,为什么一般非线性方程的解不能“叠加”,而孤立子却能保持相对稳定呢?
人们发现,具有孤立子解的方程都是非线性色散波动方程。所谓“波动方程”,是指这种方程描写的是大自然的波动过程。所谓“色散”,是指这些波动过程的各组成部分具有不同的频率,它们以不同的速度运动,这样,波行进了一段距离后,就变得“支离破碎”了。由此可见,色散是一种破坏波动过程的因素。
同样,非线性也是一种破坏波动过程的因素,因为非线性会使波动的高频率不断积累,导致这种波在行进过程中变得越来越陡峭而最终发生破碎,就像我们通常看到的白帽浪在海面破碎那样。
但是,当“色散”和“非线性”这两种破坏因素巧妙结合在一起的时候,“非线性”的高频率积累效应被“色散”的频率分散效应所抵消,它们相互制约,相互平衡,“负负得正”,竟成功地保持了波形的稳定不变,这不能不说是大自然的一个造化。
光纤通信中的孤立子
不要以为孤立子仅是数学家们的“纸上谈兵”,从原则上说,任何理论研究都会或早或迟地产生应用价值。可喜的是,孤立子的理论研究很快就在实际应用中放射出了异彩。这就是非线性光纤孤子通信技术。
我们知道,光纤通信是当今最先进的通信技术。但目前光纤通信中所用的是一种线性通信方案。光纤中传输的光信号较弱,色散使光脉冲变形,进而引起信号之间的干扰;光纤对所传输信号的损耗,使得必须在光纤线路中设置结构复杂的“光电”中继器,花费很大。
孤立子的特点是能把一定的能量稳定地集中在有限的空间内向前传输,把这个特点应用到光纤通信中,便能有效地克服目前光纤通信的这些缺点。
要产生孤立子,必须要有“非线性”和“色散”,而且要设法使这两种作用相互平衡。“色散”业已作为目前光纤通信中的缺陷而存在,因此在光纤孤子通信技术中采用了非线性通信方案,以产生“非线性”效应。具体地说,就是利用光纤折射率的非线性,同光纤中的色散相互抵消,使“光学孤子”能够超远距离地、不变形地在光纤中传输,完成通信任务。
采用光纤孤子通信技术后,通信容量将比当今最好的线性光纤通信系统高出1~2个数量级,无中继距离可达几百万米。
光纤孤子通信技术的理论研究开始于70年代,到80年代后期,有关的技术问题基本得到了解决,目前已进入实用化阶段。有人估计,到本世纪末,光纤孤子通信将取代线性光纤通信和卫星通信。
丰碑永存
1982年8月,正值孤立子研究的先驱、孤立波的发现者斯科特·罗素逝世100周年纪念,来自世界各地的从事孤立子研究的140位学者云集英国爱丁堡的海略特-瓦特大学,举行国际孤立子学术会议。8月25日下午,全体会议代表步行来到离校园不远的一条小运河边,由美国的克鲁斯卡尔和扎布斯基为竖立在一座小桥旁的罗素纪念碑揭幕。当年奇异的孤立波现象被发现后,并未得到人们的认可,罗素终于抱憾而逝,而如今,小小的孤立波已经发展成非线性科学领域中的轩然大波。人们将永远牢记罗素为此所作出的贡献。
大自然的分形几何
从刘徽割圆谈起
你一定知道圆周率π,它是圆的周长与其直径的比值,近似地等于3.1416。但π的这个近似值是怎样求出来的?这你或许就不一定知道了。在现代数学的一个专门分支——计算数学中,有许多有效的计算π的方法,但它们一般都要涉及到一些高级的数学概念。其实,有一个既直观又初等的方法,那就是我国魏末晋初时期的数学家刘徽所用的割圆术。
刘徽割圆术的基本思路是这样的:
假定有一个直径为1的圆,计算圆周率就相当于求这个圆的周长。那么怎样来求这个圆的周长呢?我们可以先画一个边长为1/2的正六边形,显然,它内接于直径为1的圆。然后作正六边形各边的垂直平分线,这些垂直平分线当然经过正六边形的中心。以中心为一个端点,在每条垂直平分线上各截取长为1/2的线段,这样,这些线段的另一个端点(共6个)连同正六边形的6个顶点就成为一个正12边形的顶点。再对这个正12边形重复上面的做法,就可以得到一个正24边形。依此类推,我们可以继续得到正48边形、正96边形、正192边形、正384边形……只要有时间和耐心,我们可以一直做下去。从图形上看,这些正多边形是越来越接近那个直径为1的圆了。因此我们可以用边数足够多的正多边形的周长来近似地作为那个圆的周长,而这些正多边形的周长是可以从最初的那个正六边形周长(等于3)开始,用勾股定理一步一步地计算出来的。
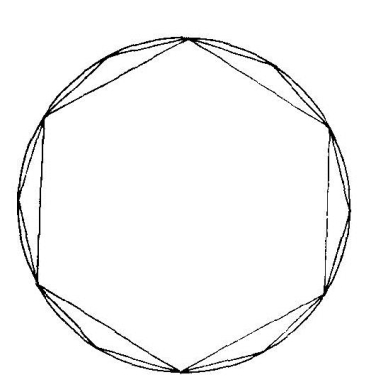
刘徽割圆术
据说,刘徽用这种方法算到正192边形,得到了圆周率π的一个近似值3.141024。这在当时是一个了不起的成就。
极限图形
在这里,刘徽用到了这样一个思想:这些正多边形是可以一个接着一个地无止境地画出来的,而且画到“最后”,正多边形就“变”成了一个圆。或者说,圆就是这一系列正多边形的“极限图形”。用刘徽自己的话来说,就是:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣。”
应当指出,刘徽的这个思想在世界上并不是首创。大约在公元前5世纪,古希腊柏拉图学派中就有人用几乎同样的方法来求圆的周长,不过他们是从圆的内接正四边形开始,相继作出内接正八边形、正16边形、正32边形等一系列正多边形,从而计算出圆周长的近似值的。这种思想后来为公元前3世纪的古希腊伟大科学家阿基米德所发扬光大,他不但考虑圆的内接正多边形,而且考虑其外切正多边形。据说他得到:
在古代东西方文化缺乏交流的情况下,古希腊和中国的数学家不约而同地想到了用一系列已知图形来“逼近”一个极限图形的方法,可见这种想法是很自然的。
“妖魔曲线”
能不能用一系列已知图形来“生成”一个未知的极限图形呢?在这里,我们把“逼近”改成了“生成”,其区别在于:当阿基米德等人和刘徽用一系列正多边形来“逼近”圆的时候,圆已经在他们心目中存在了,也就是说,圆是什么样子的,它有些什么基本性质,这些都已经很明确了;而现在,我们要“生成”的极限图形,它是什么样子的,它有些什么基本性质,我们都不知道。
这个想法是不是也很自然呢?这很难说,因为在长达2000多年的时间中,没有人想到用这个方法来生成未知的图形。然而,到19世纪,首先是德国数学家维尔斯特拉斯发现了一条“妖魔曲线”,这条曲线上的每一点都是“转折点”,也就是说,它在每一点都像多边形的边在其顶点处那样发生转折。这真有点儿让人不可思议。接着,意大利数学家皮亚诺发现了一条能填满一个正方形的也是处处为“转折点”的“妖魔曲线”。这两种“妖魔曲线”原则上都是用上述方法“生成”的。
到本世纪初,这种“妖魔曲线”大量出现。其中比较典型的是1904年由瑞典数学家科克发现的雪花曲线。
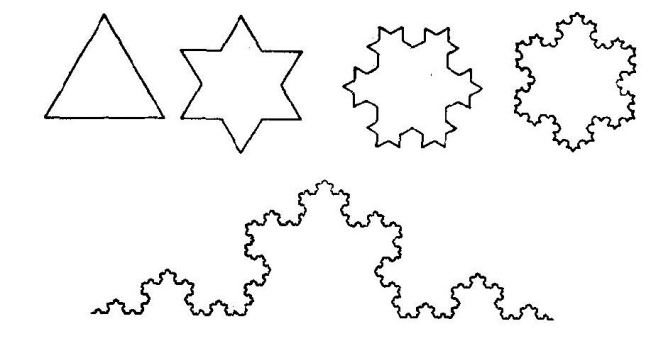
科克雪花曲线
科克的雪花曲线是从一个简单的正三角形开始生成的。首先以这个三角形每条边中间三分之一的那条线段为底边,向外作一个小正三角形,然后抹去小正三角形的底边,这样,就生成了一个六角形。以后对每次生成的图形都作如此处理(即在图形的每条边上都向外作一个小正三角形,并抹去它的底边),以至无穷。于是,一条奇妙的雪花曲线便生成了。
科克雪花曲线有一些出人意料的性质。它是一条处处是“转折点”的曲线,它的长度为无穷大,但它围成的面积却是一个有限的数值——最初那个正三角形的8/5。更重要的是,这种曲线虽然十分复杂,我们根本不可能把它画出来(我们在图中所表示的仅是它生成过程中开头的几个图形),但它的任何一段都是相似的。也就是说,如果用一个放大镜去“看”它的一段曲线的话,不管这个放大镜的放大倍数是多少,我们“看”出来的曲线形状都是一样的。这个重要的特点称为“自相似”。“自相似”说明这种曲线是不分层次的,即在任何一个层次上,这种曲线都是一样的。

谢尔宾斯基“垫片”
除了科克雪花曲线这类“妖魔曲线”外,本世纪初还出现了“妖魔”平面形和“妖魔”立体形,最著名的要数俄国数学家谢尔宾斯基给出的谢尔宾斯基“垫片”、谢尔宾斯基“地毯”和谢尔宾斯基“海绵”。一时间,“群魔乱舞”,令数学家大伤脑筋。

谢尔宾斯基“地毯”
摒之门外
为什么这些“妖魔”图形会使数学家大伤脑筋呢?原来,几千年来,专门研究各种图形的数学分支——几何学,都是以规则而光滑的图形为对象的。如我们在中学里学的平面几何,研究的主要是直线、多边形和圆;立体几何研究的是平面、多面体和球;平面解析几何研究的则是一次曲线(直线)和二次曲线(椭圆、双曲线和抛物线)。就是近代的微分几何、代数几何、拓扑学,研究的也是光滑的具体图形和抽象图形。但现在这些“妖魔”图形,没有一处是光滑的,经典的数学工具完全用不上,数学家们还能对它们做什么呢?

谢尔宾斯基“海绵”
于是,数学家们给这些图形一个“恶号”——“病态”图形,并把它们摒之数学宫殿的大门之外。是的,我们研究的是“健康”的、“正常”的图形,这些“生了病”的图形,不在我们的考虑范围之内。
物体形态的另一种抽象
我们知道,几何图形是现实世界中物体形态的一种抽象,而且同一物体,随着我们考虑问题的层次的不同,可以被抽象为不同的几何对象。就拿我们所在的地球来说吧,当我们在太阳系层次上考虑它围绕太阳的公转时,我们把它看作是一个点;当我们考虑它的自转时,我们又把它看成一个球。然而当我们考虑地球表面的地形时,那绵延起伏的重山峻岭、那一落千丈的悬崖峡谷、那奔腾咆哮的大江急流、那波涛汹涌的深海汪洋,又怎能用光滑的球面来模拟?因此,素以精确严谨著称的经典几何学,研究的事实上是物体形态在一定层次上的一种理想化的抽象形式。当然,几千年来的实践证明,这种抽象使我们得到了许多非常符合实际的结论。
但是,自然界中还有许许多多的物体,它们的形状是极不规则的,如蜿蜒曲折的海岸线、起伏不平的山脉、变幻无常的浮云、令人眼花缭乱的满天繁星,它们也需要一种几何形式来模拟。
在自然界中还存在着一些物理现象,它们的机理同时涉及不同层次上的运动状态,把它们固定在某一层次上考察是不能得到什么有意义的结果的。例如自然界中极为普遍的、看起来十分紊乱的湍流,它在宏观上的流体运动能量,经过大、中、小、微等许许多多层次上的旋涡,最后转化为分子层次上的热运动。这种状况,用经典的模型是无法描述的,它也需要一种不分层次的几何模型来模拟。
现在我们已经知道,这种几何形式或几何模型不但存在,而且就是曾被数学家摒之门外的“病态”图形。如果说,规则而光滑的几何图形是对客观物体形态向简单化方向进行抽象的结果,那么,上述“病态”图形可以说是对客观物体形态向复杂化方向进行抽象的结果。
于是,一门全新的几何学——分形几何学,便在本世纪70年代诞生了。
曼德尔布罗与分形
虽然上述“病态”图形——现在人们称之为“分形”——早在上一世纪就为人们所发现,但是分形几何学的创始人当推当代美籍法国数学家曼德尔布罗。1973年,他在法兰西学院讲课期间,提出了分形几何学的思想。他并且为“病态”图形正命,创造了fractal一词来命名这门几何学所研究的对象。fractal与英语中的fraction及fragment具有相同的词根,据曼德尔布罗的解释,意为“不规则的”、“支离破碎的”。我国大陆地区的学者经过这几年的切磋,现在认为把它译为“分形”比较妥当。
分形几何学借助经典几何学中的一些概念,发展起了自己的一套研究分形的数学工具,其中最主要的就是“分维”。
分维是由经典几何学中的“维数”概念发展而来的。我们知道,在直线上,只有长度这样一个度量,因此我们说直线是1维的,类似地,一般的曲线也是1维的;在平面上,有长和宽两个度量,于是我们说平面和平面图形是2维的,类似地,一般的曲面也是2维的;在空间,则有长、宽、高三个度量,于是空间和空间立体图形是3维的,我们常说3维立体空间,就是这个意思。我们看到,在经典几何学中,维数只能取1、2、3这些正整数。
在分形几何学中,分形的维数称为“分维”,它们可以取为正实数,而且有着好几种不同定义的分维。如在某种分维定义下,科克雪花曲线的分维近似地等于1.2618,谢尔宾斯基“垫片”的分维近似地等于1.5849,谢尔宾斯基“地毯”的分维近似地等于1.8927,谢尔宾斯基“海绵”的分维近似地等于2.7268。
比较这些分形以及它们的分维,可知这种分维是分形复杂程度和空间填充能力的一种量化描述。其他一些分维则从不同的角度刻画了分形的各种特征。
这20多年来,在科学家们的持续努力下,分形几何学的发展十分迅速。它不但在理论研究方面取得了不少重要成果,而且在大地形貌、晶体生长、晶界形貌、催化剂结构、材料断裂机理、凝聚体结构、人体血管分布等方面的研究中得到了广泛的应用。特别在计算机图形生成技术中,用分形几何学原理由计算机绘制出来的图画,别有风味,奇妙无比,可自成一艺术流派。
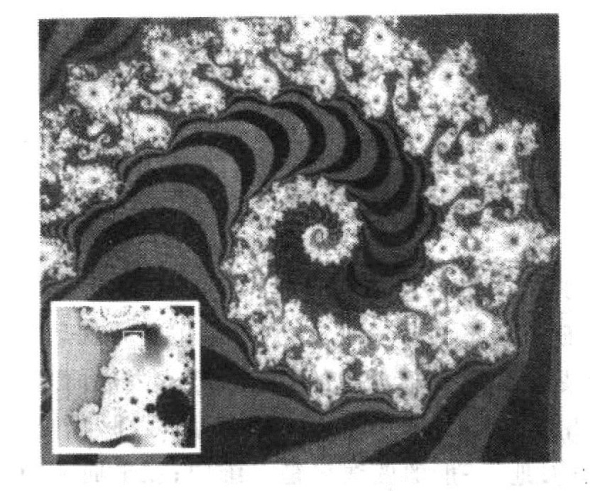
计算机生成的分形图案
分形与非线性
我们在《蝴蝶效应》中曾指出,非线性现象的特点之一是它不能容忍一丁点儿的误差。这个特点也可以说成:非线性过程对初始条件十分敏感。也就是说,只要初始条件有极微小的不同,相应的非线性过程发展到后来就可能会大相径庭。但是,我们又说,非线性过程在总体上还是有规律的。为了探索这种规律,从事非线性科学研究的科学家们就根据非线性过程发展的大致性态对相应的初始条件进行分类。
如果在一个坐标平面上考察初始条件,也就是说,把初始条件表示为坐标平面上的点,一个初始条件对应坐标平面上的一个点,那么,一类初始条件就对应着坐标平面上的一个点的集合。科学家们发现,这些集合在一般情况下就是分形。这样,分形就与非线性科学的研究结上了缘。
其实这也不奇怪。非线性过程是客观世界复杂性的一种表现,而分形则是对客观物体形态复杂性的一种几何模拟,它们之间的联系是十分自然的。如今,在非线性科学研究中,几乎处处遇到分形,分形几何学已成为这个研究领域的必不可少的数学工具。
人类自诞生以来,一直同大自然打着交道。人们不断地探索自然,认识自然。在这一过程中,科学家们以无比的献身精神,以百折不挠的斗志,建立起了庞大的自然科学体系,为人类进一步利用自然、改造自然打下了基础。但是,茫茫宇宙,未揭开之谜是如此之多,而且随着对自然界的不断探索,新问题也在不断地涌现。因此,这种探索是永无止境的。然而,正是在这永无止境的探索中,人类不但逐步地认识着自然,不断地改造着自然,同时也改造着人类自己,从而创造着灿烂辉煌的文明。这本小册子限于篇幅,仅介绍了当今自然科学前沿研究的一部分基本问题。但相信这些介绍,能帮助读者了解自然科学的研究特点和她那艰难曲折的历程。若能引起读者对自然科学知识的兴趣和进一步探求,这将是我们最大的期望。
