一个简单的社会影响模型
如果你认为自己是果断而独立,不会随波逐流,你可能高估了自己的判断力。心理学家Stanley Milgram(对,就是那位以权力服从实验和六度分离理论而闻名于世的社会心理学家!)和他的合作者们在上世纪六十年代末在曼哈顿市中心做了一项实验。在实验中,他们安排了数量不等的实验助手,让其假装为路人朝高楼张望,当然高楼上并没特别之处,而Milgram则在远处观察和记录路人的行为。实验结果发现匆匆而过的路人通常也会驻足张望,而安排的助手越多,停下脚步的路人也越多。社会心理学家Bibb Latane在八十年代初重新分析了连同Milgram实验在内的十多项群体心理的工作,发现几条有意思的规律。社会影响随着周遭人群规模变大而变大,但这种规律并非线性。第一个人对我们的影响是最大的,而后面每加一个人的影响总小于前面一个人。而第20个安插的实验助手对路人的影响几乎可忽略。这种关系的数学表达即是幂率关系(I~Nβ,其中I为个体受到的社会影响程度,N为周遭所持该行为的人群规模,β为介于0,1之间的指数。在Milgram的实验中,β=0.24)。
当然,对于Latane所谓“社会影响”(social influence)并不仅局限于行为模仿(别人驻足朝天张望会增加自己做同样行为的可能性),他发现幂率规律广泛地存在于各种社会行为中。比如当众演讲或表演时,我们都会或多或少的“怯场”,即面对观众时产生的紧张与焦虑,而紧张程度与观众规模的大小紧密联系。实验发现,口吃患者在面对0,1,2,4,8名观众朗诵时,因结巴而读错的字也与观众规模成幂率关系。观众越多,结巴程度越严重,而当观众的数量大到一定规模后,结巴程度并未显著增加。再比如,在遇见灾难或不公事件时,个人勇于站出来承担社会责任的可能性会随着所在群体规模的增加而以幂率降低。这即所谓旁观者效应(bystander effect)。2011年发生在广东佛山的“小悦悦事件”即为旁观者效应的典型案例。2岁女孩小悦悦被汽车撞到并被压在车下,之后的18名路人无一出手帮助,直到第19位路人救起小女孩,随后将其送往医院急救。是国人人性冷漠么?不尽然。类似的著名的旁观者悲剧也发生在纽约和加利福尼亚。Latane在七十年代通过一系列实验证实,当只有你一个人在场的时候,你更容易挺身而出,帮助受难者。但若周围有多位旁观者的时候,你的责任感就“稀释了”,即你伸出援手的可能性大为降低,而这可能性也受幂率支配。
除了周遭群体的规模,个人受到的影响也取决于对方的社会地位,权力,可信度,声望等。我们把这些因素称为影响源强度。影响源强度永远是相对的,因人而异,也因时因地而异。对于一个二年级有厌食症的小女孩,比较有效的改进方法可能不是父母的叮嘱和教导。如果把她与另一个三年级的小女孩组成“lunch buddy”,也许会有意想不到的成效,因为相对于父母,年级稍高的同龄人更能成为参照组。Latane将这个简单的社会影响模型称之为电灯泡模型(light bulb model;见图:4-1)。我们受到的社会影响不是受到某一个变量的控制,而是多个效应的综合。图中我们可以看到影响个体的因素有周遭人群的规模(圆圈数量),源的影响强度(圆圈大小),以及社会关系的强弱与远近(箭头长度与宽度)。在我们做出“理性的”决定前,无论是换何种手机,使用什么样的语言,或是否决定戒烟,我们的潜意识里已经在不同程度上受到了来自他人的影响。这种综合的社会影响可能通过改变我们的注意力,记忆或态度等认知能力来改变最终的决定。其中Source为影响源,即周遭的人群。Target为被影响的个体。图3-1中圆圈数量代表周遭人群的规模,圆圈大小代表源的影响强度,而箭头长度与宽度代表社会关系的强弱与远近。
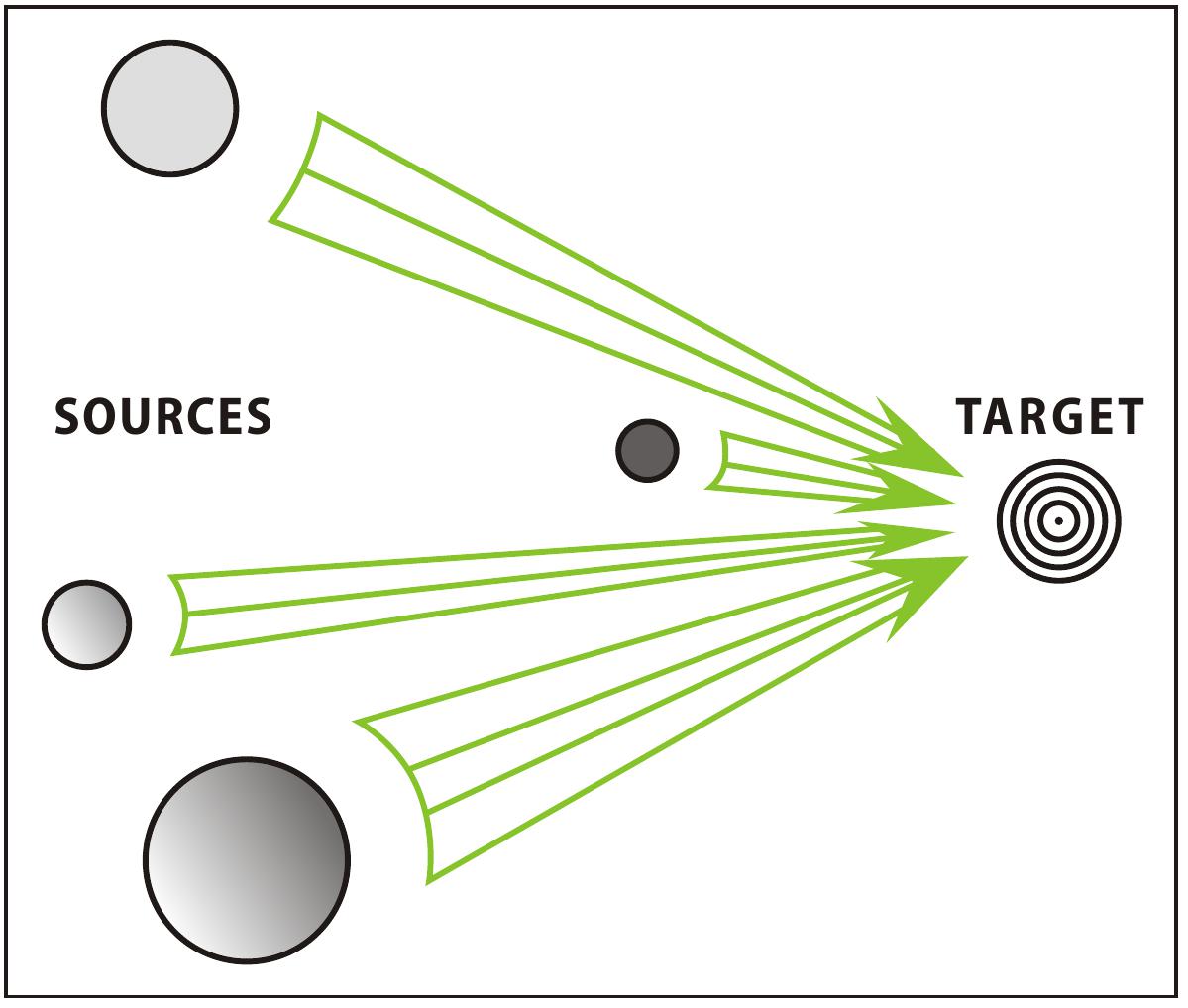
图4-1 社会影响的电灯泡模型
