用社群结构理解“朋友即限制”

我们来讲一个数学故事，有一个农场主拉着自己的奶牛在集市上竞猜，集市上的人如果猜中了奶牛的体重，就把奶牛送给他，路过的人纷纷上前猜测奶牛的体重，统计人们给出的猜测值，发现猜的人越多，猜的人的均值就越逼近奶牛真正的质量，现在来思考一个问题，为什么人越多，均值越逼近奶牛真正的质量呢？你会想到什么，可能有人会想到“正态分布”，正态分布是社会中最常见的一种分布状态，集市上的人们猜测数据的集合很可能服从正态分布，正态分布的均值会不断接近真实值，这个猜测是正确的。在猜奶牛体重的过程中，人们心中会不自觉的把奶牛的体重和自己熟悉的东西的体重相比，可能汤姆的家中刚好有一只奶牛比农场主的奶牛要大一些，那他就觉得奶牛体重应该低一点比较准确，但是低多少呢，不知道，而杰克的家中的奶牛比农场主的奶牛小一些，他就会猜的高些。所以，猜测值相比于真实值可能会大也可能会小，那集市上的人会一直猜的比真实值都大吗，显然不可能，会猜的一直比真实值都小吗，好像出现这样结果的概率也比较小。可能猜多猜少的人近乎一半一半，如果是这样，猜多猜少的部分互相抵消，最终的结果就接近奶牛的真实体重了。

Joshua Becker与Damon Centola等人仔细地研究了“人越多，越能够得到真实值”的这种现象，他们发表在美国国家科学院学报（PANS）的论文《Network Dynamics of Social Influence in The Wisdom of Crowds》中，描述了一项猜泡泡糖的实验。在一个杯子里，放满球形的泡泡糖，邀请很多人过来参加实验，这个实验好像参与实验的人中一部分吃过一模一样的泡泡糖，一部分人没有，实验者根据猜测结果，发现人们在猜的过程中形成了两种社群结构：中心化社群结构与非中心化社群结构。对于中心化结构，群体的猜测结果与中心的人的猜测结果保持一致，如果中心的人猜测比较准确，人们的猜测会越来越接近事实，否则，人们会越来越远离事实，中心的人引导了整个故事的发展，领导的方针正确，公司、国家就会发展的越来越好，否则就会衰落。而对于非中心化结构的社群，没有领导，所以大家的想法是发散的，群体内部人与人之间的影响不大。

图5-2　猜测杯中泡泡糖数量的实验⁽¹⁾

为什么要讲这两个故事呢？其实是想回到最初我们提出的观点：朋友即限制。这两个故事放在一起可以帮助我们去思考，社交圈的限制性与社群内部联系之间的关系。如果是中心化结构的社群，领导人的思想会限制在这个群体里的所有人的思想；而如果是发散型的社群，人们之间的限制关系很弱，一个人有过激的想法不妨碍另外一个人有过于保守的想法，最终，这类社群整体得到的想法将会比较中庸。

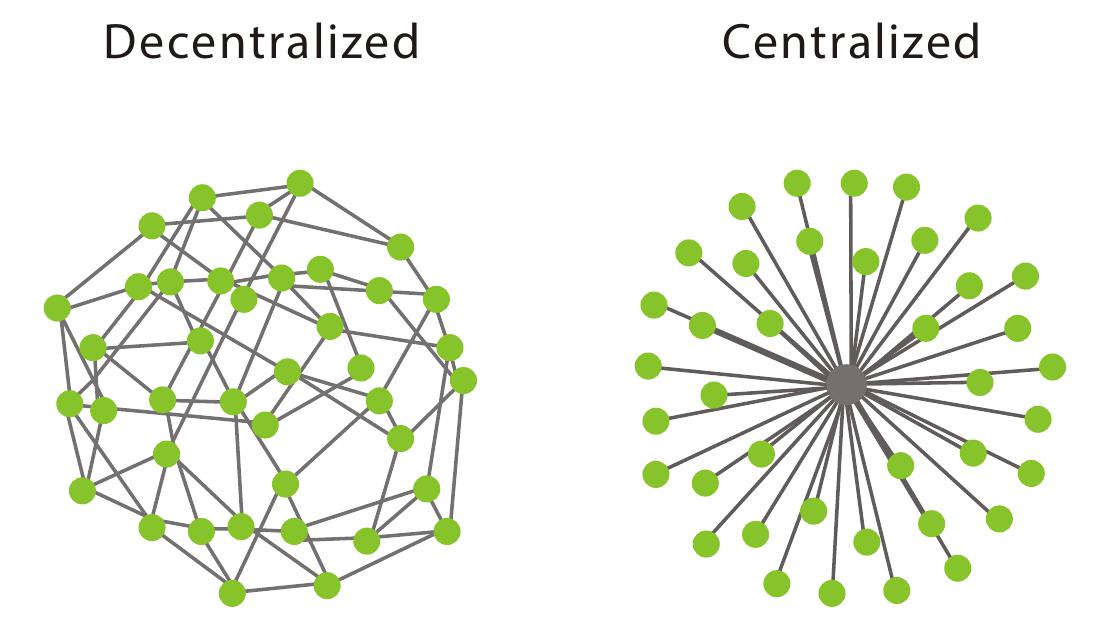
图5-3　两种社交圈的结构