研究工具与方法
本研究在电子科技大学信息医学中心完成。使用GE Discovery 750 3.0-T磁共振系统完成BOLD信号的采集。在开始实验前,我们利用相关问卷详细询问被试的身体与健康状况(如体内是否有金属植入物、体表是否有文身、是否有空间幽闭症等),根据问卷结果剔除身体条件不符合接受磁共振扫描的被试。所有被试在进入扫描前均没有进行任何舞蹈片段的训练。为了保障实验安全与扫描效果,通过筛选的被试在进入扫描前,需要被试换上扫描专用的服装,去除身上的所有金属物品,并接受实验人员使用金属探测仪进行检查确认。被试进入磁共振扫描仓,以尽量舒适的姿势平躺在其中。为了减少头动对数据的影响,实验人员告知被试在整个实验过程中尽量保持头部不动,并使用泡沫固定其头部。为了减少无关任务对BOLD信号的影响,被试要求全程闭眼并被告知尽量避免睡着。实验人员为被试戴上专用耳塞,从而减少机器扫描时的噪音对被试的影响。被试的静息态功能图像扫描使用一个8通道的头部线圈采集,其静息态功能MRI图像由回波平面成像(echo planar imaging,EPI)序列获取。扫描参数为:重复时间(repetition time,TR)=2000ms,回波时间(time echo,TE)=30ms,反转角(flip angle,FA)=90°,扫描视野(field of view,FOV)=240×240 mm2,扫描矩阵(acquisition matrix)=64×64,扫描层数(slices)=32层,扫描厚度(slice thickness)=4 mm(无间隔),体素大小(voxel size)=3.8×3.8×4 mm3。所有被试接受510s的静息态扫描,产生255个体素(每个体素32层)。随后,使用三维快速扰相梯度回波序列(T1-3D FSPGR)采集被试的高分别率T1像。TR=6.008ms,TE=1.984ms,FA=9°,matrix=256×256,FOV=25.6×25.6cm2,扫描厚度=1 mm(无间隔),152 slices。
进一步,我们对研究被试的静息态功能磁共振数据进行处理与数据分析,主要使用功能连接密度计算分析,获取舞蹈家脑内功能连接密度差异区域,进而以以上差异区域为种子点,计算种子点与全脑的功能连接。
(一)fMRI数据预处理
使用SPM8(Statistical Parametric Mapping,http://www.fil.ion.ucl.ac.uk/spm/so ftware/spm8)软件对磁共振数据进行处理。转换DICOM格式的数据为NIFTI格式的数据;丢弃最初5组的数据,避免扫描初始时不稳定因素干扰,建立磁化均衡性;时间校正与头动校正;使用蒙特利尔神经研究所标准人脑模板空间(Montreal Neurological Institute,MNI)系统中的EPI模板对图像进行标准化,然后以3mm×3mm×3mm大小的体素重采样;信号滤波(0.01~0.08 Hz);回归噪音信号(6个头动参数)。空间平滑的主要处理步骤,即使用全宽半高值为8mm的高斯核函数与回归噪音信号(白质、脑脊液、全脑信号),并未在功能连接密度分析中使用,但是在功能连接分析中使用这些步骤。近期研究发现,头动对功能连接有较大影响(Power et al.,2012,Satterthwaite et al.,2012),因此,我们删除了主要方向上的头动超过1.5mm或是角度超过1o的被试的数据。另外,我们使用公式4-1对两组被试头部的平移与转动进行分析。
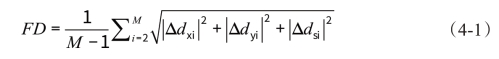
式4-1中,FD是平均头动,M是时间进程的长度(M=250),xi、yi与zi分别为在第i次时间点x、y和z的方向,Δdxi=xi-xi-1,对于yi与zi也如此。
(二)短程与长程的功能连接密度分析
静息态功能连接是一种研究人类大脑可塑性的良好工具(Fox&Raichle,2007)。前期已经有许多研究利用rs-FC分析特殊技能训练所导致的脑功能可塑性改变,尤其是经过长期训练拥有高水平技能的专家,如音乐家(Luo et al.,2012;Li et al.,2014)、高水平运动员(Huang et al;2015)等。近期,随着功能连接分析方法的发展,功能连接密度(FCD)成为一种新的数据驱动研究方法。该方法通过由时间相关和空间连接双重约束的基于体素的功能网络分析,有效地刻画人脑内基于体素分布的长程与短程功能连接密度(Tomasi&Volkow,2010),进而可以实现对全脑的网络度中心性的定义(度中心性是衡量大脑特定体素的网络局部中心性的一个网络属性指标)。相较于基于种子点的功能连接分析方法,功能连接密度避免了定位种子点的偏差。在FCD计算中我们设定大脑灰质模板约束下的大脑体素为节点。针对功能磁共振数据,使用皮尔逊线性相关系数在时域上定量测量各个节点间的功能连接强度。通过在时域上连接强度和每个体素与其他体素空间连通性的双重约束,计算得到大脑静息态功能磁共振短程功能连接密度和长程功能连接密度图谱。
根据Tomasi与Volkaw的方法(Tomasi&Volkow,2010;Tomasi&Volkow,2011),我们使用自编写的程序来估计个体的基于体素的功能连接密度图谱。具体计算流程如下:(https://www.daowen.com)
步骤一:在时域功能连接强度方面设定大脑体素间的约束规则,用于确定大脑每个体素全脑连接个数。在大脑灰质模板内通过皮尔逊相关计算确定特定体素与全脑体素功能连接强度。根据以往研究设定阈值(r=0.6)用于确定全脑连接体素个数N。通过循环运算得到基于体素的全脑功能连接个数图谱。
步骤二:设定体素的空间连通性规则进而得到全脑体素的短程功能连接密度图谱。基于第一步计算得到的目标体素全脑体素连接个数图,在时域连接约束下,在空间上确定与目标体素局部空间连通区域。进而得到目标体素短程功能连接体素个数N_short。通过循环计算得到大脑灰质模板内体素的短程功能连接个数图谱。
步骤三:在前两步分析的基础上,计算灰质模板上各个体素的长程功能连接密度图谱。针对大脑内每个体素,通过计算其全脑连接个数与短程功能连接个数的差值得到目标体素长程功能连接体素个数:N_long=N-N_short。通过循环运算得到基于体素的全脑长程功能连接个数图谱。
步骤四:进一步针对被试短程和长程功能连接密度图谱进行个体图像标准化计算:全脑每个体素的连接个数值除以个体全脑灰质模板内平均连接个数值,得到体素的空间标准化k值,进而通过对大脑连接密度图谱的空间进行平滑处理以减少被试间大脑功能解剖差异性。
(三)基于种子点的功能连接分析
根据前面FCD的结果,我们以FCD全脑组间差异区域作为种子点,进一步计算基于种子点的全脑功能连接图谱。针对预处理之后的图像数据,我们首先从种子点抽取平均时间序列;然后使用皮尔逊相关,计算种子点与全脑所有体素间的线形相关。通过这种方式,制作每个被试的关于差异种子点的功能连接图谱。为了使组上统计数据(相关系数)分布近似高斯分布,我们对相关图谱进行费希尔Z变换。在SPM8中我们进一步使用基于体素的双样本t检验,来进行功能连接图谱的统计分析。
(四)功能连接特性与舞蹈训练变量间的相关分析
我们使用皮尔逊相关分析,对舞蹈组被试舞蹈训练时间与改变的脑功能连接(单个脑区的FCD和脑区间的功能连接)进行相关分析。首先,我们将舞蹈训练变量(每周平均训练时间、开始学习舞蹈的时间、舞蹈累计训练时间)与感兴趣区(Region of Interest,ROI)功能连接密度的k分数做相关分析。进一步,我们计算了改变的功能连接与舞蹈训练变量间的线性相关性,即将每一个改变的功能连接平均z分数与舞蹈训练变量进行相关分析。
