研究工具与方法
（一）基于纤维束示踪的空间统计分析
笔者利用磁共振弥散张量成像（Diffusion Tensor Imaging，DTI）的基于纤维束示踪的空间统计分析（Tract-based Spatial Statistics，TBSS）技术，对舞蹈家、音乐家与正常对照组进行比较研究，寻找舞蹈家与音乐家脑白质纤维束微结构的差异。DTI是在弥散加权成像基础上发展而来的磁共振成像新技术，它能够对大脑细微结构进行定量分析，尤其对大脑白质纤维的成像具有良好分辨性。自由水分子具有随机不规则的弥散性，但在人体组织中由于组织结构的不同将影响水分子自由弥散的方向和速率，因此，水分子的弥散表现出不同程度的各向异性。例如，在白质纤维束中，水分子更倾向于顺着纤维束的方向弥散，具有更高的各向异性。因此，可以根据分析三维空间内白质纤维组织内水分子的弥散特性，反过来追踪刻画白质纤维的形态特征。
在描述弥散程度时，一般用椭球模型来表示。如，纯水中水分子的弥散程度在三个方向上半径相同，因此是一个圆球，其水分子弥散各向异性为零。水分子弥散的各向异性越高，其主要弥散方向上的半径越大，因此，愈发地表现出一种椭球形状，如图5-3所示。
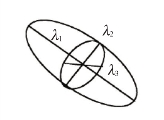
图5-3 弥散度椭球模型
在弥散张量成像研究中，常常使用平均弥散率（Mean Diffusivity，MD）和部分各向异性（Fractional Anisotropy，FA）两个指标来进行描述。其中，MD为椭球模型中三个方向的弥散系数的均值，它反映水分子的弥散水平和弥散受阻情况，但无法刻画弥散的方向。MD值的大小反映出组织中所含自由水分子的多少，如，脑脊液中自由水分子含量高，其MD值很大，而白质纤维所含自由水分子量低，其MD值较小。
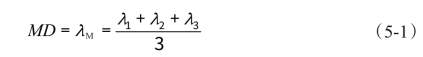
式5-1中，
为椭球模型中三个方向的弥散系数的均值，λ1、λ2与λ3分别为椭球模型中三个方向的弥散系数。
FA值反映的是水分子各向异性成分占整个弥散张量的比例，具有大小与方向，可以刻画出人体组织的结构方向。如，脑脊液的水分子运动接近自由运动，其FA值基本为0，而脑白质纤维因结构的规则排列，其FA值接近1（Le Bihan et al.，2001）。因此，在本研究中我们选取MD值与FA值两个指标来对白质纤维结构进行刻画。选择MD值是因为它能够全面反映体素或区域的弥散状况，选择FA值是因为其信噪比较高，可以反映清晰的灰质白质对比。因此，TBSS统计分析将两种指标结合起来，综合描绘纤维束微结构的变化情况。
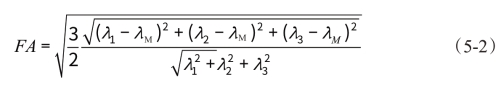
本章中实验工具与实验过程详见第四章。其中，DTI数据使用单次、自旋回波、回波平面序列采集。具体扫描参数设置为：重复/回波时间（repetition time/echo time，TR/TE）=8500ms/70ms；扫描视野（Field of View，FOV）=256×256 mm2；体素大小为2×2×2 mm3；76个轴向切片；64个弥散梯度方向；b=1000 s/mm2，获得全脑DTI数据。
（二）数据处理与分析
采用MRIcron工具包将每个被试的DTI数据转化为4D NIFTI格式的图像。使用FSL（FMRIB Software Library，v5.0；Jenkinson et al.，2012）的BET工具包从dMRI数据中去除非脑组织，并产生各自的脑内Mask；使用FSL中的FDT工具进行涡流和头动校正；使用FDT中的DTIFIT工具，应用弥散张量模型计算每个体素点的各个弥散参数，如三个特征向量（λ1、λ2、λ3）、部分各向异性分数及平均弥散率。在本次实验中，我们主要考察了FA值和MD值，以衡量舞蹈与音乐训练对大脑主干纤维束白质微结构指标的影响。
使用常规TBSS计算流程（Smith et al.，2006），对被试FA图谱进行体素级别的统计分析，如图5-4所示。具体步骤如下：将所有被试的MNI空间的FA图谱平均，生成组平均FA图谱；阈值设为大于0.2，将所有被试的FA图谱填充到由组平均FA图谱导出的FA骨架图谱上；类似于FA图谱，MNI空间的MD图也被投影到骨架上用于进一步的统计分析；在一般线性模型框架内，使用基于排列的非参数检验（迭代置换5000次）进行单因素方差分析，以及非参数事后检验以考察两组之间的详细差异，其中控制变量是舞蹈组和对照组；最后，采用无阈值聚类增强校正（Threshold-Free Cluster Enhancement，TFCE）的方法进行多重对比校正（Smith&Nichols，2009）。根据约翰·霍普金斯大学的白质图集模板（JHU ICBM-DTI-81 White-matter Labels），确定差异区域的所属白质纤维结构的部位。
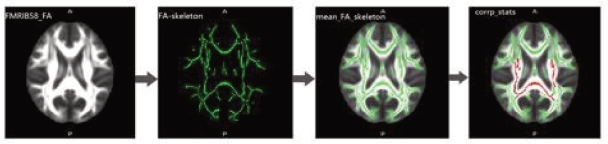
图5-4 基于纤维束示踪的空间统计分析步骤