4.3 最小候选检测器集合
B细胞作为无差异的干细胞在骨髓中产生，最初的差异来自于基因（决定着抗体的片段）的重新排列，该过程（与抗原的出现无关）不断地提供先天的B细胞。先天的B细胞群不与自身发生反应，并以最小的交叠代价完全覆盖非我空间，使免疫系统能对几乎所有的抗原进行不同程度的识别。相应的，在本模型中也有一个类似的起源处理过程，采用最小候选检测器集合类比于免疫系统中先天的B细胞群，以最小的交叠代价完全覆盖整个入侵检测的问题域。
定义4.11：最小候选检测器集合M。在给定ε条件下（0＜ε＜1），任一检测器di的识别域为
，在满足任一
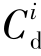不与自我空间S相交的前提下，
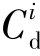以最小的交叠代价覆盖非我空间N，有：
其中k为M的势，即｜M｜=k。
由于M中的任一检测器不与自我空间S相交，所以M是有效的候选检测器集合。新检测器的产生可以无须经历否定选择过程，而是直接产生于M，如果能实现这样一个检测器集将有助于极大地降低模型的训练时间和网络入侵的检测时间。相邻的检测器之间识别区域交叠，我们定义识别域中未交叠区域为d的空间覆盖域C，定义如下。
定义4.12：检测器d的空间覆盖域C。检测器d的空间覆盖域C在不与自我空间S相交的前提下，定义如下：
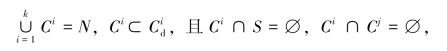
其中i，j=1，2，…，k，i≠j。
C为n维的超级立方体，位于区域Cd内，则C的空间体积CV定义如下
图4-1 检测器的空间覆盖域
虚线框表示检测器的空间覆盖域C，而两个实线球形
分别表示检测器di和dj的识别域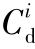
和
其中n为模式空间的维度。当n=2，C的平面示意图如图4-1所示。检测器di和dj相邻，它们的识别域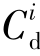
和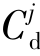
叠交，存在公共的部分，在公共部分内的模式（如图4-1中的s2或s3）对检测器di和dj同时形成刺激作用，我们称为交叉刺激，交叉刺激区对应于那些在Cd区域内但在C覆盖区以外的点，至于哪个检测器能胜出则由活化概率函数决定。
我们假设已知非我空间N的空间体积为NV，根据公式（4-5），最后完全覆盖整个非我空间N所需的最少检测器数L为：
其中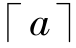
为浮点数a向上取整，以至在小范围内相邻的覆盖域Ci∩Cj≠∅，可以保证非我空间N中的任何一点至少能被一个检测器识别，有L≥k。
为了使新的检测器能直接产生于M，免疫模型首先需要初始化并存储M，然而由公式（4-5）和（4-6）可知，随着空间维度n增加或ε的变小，M的规模成指数式膨胀，因此M的计算与存储成为模型初始化化过程中首要解决的问题。
为了简化问题的复杂性，我们假设在自我空间S=∅、非我空间N=U的特殊情况下来定量描述M的规模，即
由定义4.4可知，模式空间U的体积UV可以认为近似等于1，N=U则有非我空间的体积NV≈1。
第三章中我们选取了网络连接的8个特征属性，并转换到一个14维的单位度量空间，经过数据降维处理后空间维度n=9，表4-1给出了在阈值ε取不同值的情况下L的值。
表4-1 在ε取不同值时L值
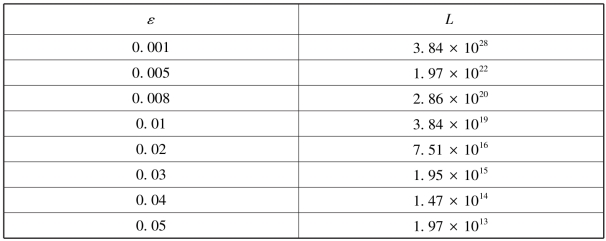
表4-1显示随着ε的减小，而
成指数式递增，反之亦然。显然计算与存储每一个检测器的特征向量（浮点数）所需的系统开销巨大，这在有限资源环境中是不现实。
根据本模型中检测器的特性，我们提出利用检测器的空间位置来描述MS=∅的简化方案。d∈N的空间覆盖域C⊆N为n维的超级立方体，所以d的空间覆盖域C在每一维坐标轴上的间隔大小h为：
由定义4.4可知，U是一个n维的单位特征度量空间，则U在各维方向上的张量或长度I=1，因此我们根据式（4-7）可以计算出在每一维坐标轴上检测器的个数l：
例如n=3和ε=0.08时，则CV=7.9×10-4，由式（4-7）和式（4-8）分别得h=0.092，l≈10.82，l的3次方约等于L。
我们对集MS=∅中每一个元素在各维坐标轴上的位置进行排列编号（从0到L-1），然后将其转换为空间坐标表达形式（a1，…，an），其中ai为整数且0≤ai≤
-1（i=1，…，n），记为整数索引空间A：[0，
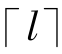-1]n。已知检测器d在A中所处的位置，可由下式计算其在U中各维的特征向量值xi：其中ai为A中第i维的坐标值。
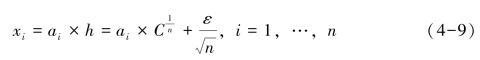
例如已知MS=∅中某一个检测器dj在三维索引空间A中的位置为（5，6，7），则由公式（4-9）可计算出其特征向量为
0.609，0.720）。因此阈值ε确定下来后，最小检测器集MS=∅中每一个检测器的特征向量
也可随之确定下来。
由上分析，免疫模型无须初始化与存储MS=∅中每一个检测器的特征向量，只需计算与存储h和l的值，并由l产生索引空间A即可，每当免疫模型产生新的检测器时，随机在整数索引空间A中选择一点，由公式（4-9）即可得到新检测器的特征向量，算法的时间复杂度与｜MS=∅｜无关，因此MS=∅的初始化与存储问题可以得到解决。
上述的分析结果是在S=∅、N=U的假设环境中得出的，同样也适用于S≠∅的实际环境，因为在免疫模型中，非我空间N虽是未知的，但自我空间S是可预知，由定义4.5可知，N随S的确定而确定。
S≠∅意味着由A中的某些点产生的检测器会发生自身反应，需要避免对这些点的选择。而对这些点的确定，就需要首先确定自我模式在模式空间U中的分布，即S的确定，S可以通过正常模式集即训练集Strn来获得，因此S是可预知。由Strn来界定S的边界，通常的方法是采用聚类的算法，即根据某种准则，将样本空间中的样本数据集合划分为表示不同模式或系统行为的一些子集，使得同一子集中的对象尽可能相近，不同子集之间的对象尽可能相异，聚类算法能较精确的描述样本的空间分布，如分类的个数、各类的中心和各类包含的样本数量等细节。下面结合本模型的特点和要求，就自我空间S的界定方法进行研究。