5.3.1 检测器的活化概率函数
定义5.1:检测器d的活化概率。检测器在某一时刻被激活的概率受到两个方面因素的影响:d识别域内异常事件的直接刺激和d邻域内异常事件的间接激励。
![]()
式中:α为调节系数;a(d,Ti)为Ti时刻d识别域内的异常事件数量;k(Ti)为激励函数。
式(5-4)中引入了3次幂函数(非线性函数),目的是d的活化概率将随着其识别域内异常事件数量的增大而非线性地快速趋于1,调节系数α和激励函数k(Ti)控制概率曲线的斜率,α或k(Ti)越大斜率越陡,k(Ti)=1意味着无激励作用,设α=0.001时,则P(d,Ti)如图5-4所示。
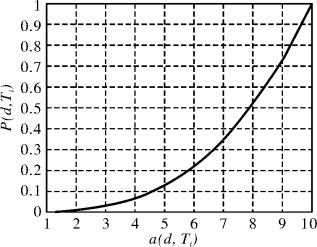
图5-4 Ti时刻检测器的活化概率示意图
k(Ti)=1,α=0.001,且当a(d,Ti)≥10时,P(d,Ti)=1。
入侵行为往往是由某一段时间内的异常事件序列组成,即入侵行为具有时间的关联性,通常以2秒为时间窗口对某一网络行为的连接记录进行扫描,可以得到该网络行为基于时间的统计特征,也可以避免因偶然的事件或噪声数据而影响模型的判断。因此在本模型中异常模式一旦被模型呈现出来,被赋予一个生命周期tab,设定为2秒,同样由此而产生的初始检测器也被赋予一个生命周期T-I(其中I代表初级生命周期,以区别于其他类的检测器)且T-I>tab,记初始检测器为dT-I。检测器与异常事件的生命周期如图5-5所示。
图5-5中abi(i=1,2,…)为检测器识别域内的异常事件。当检测期的某一时刻Ti,系统呈现一个异常模式abi被某一dT-I捕获,即检测器受到最新的一次刺激,式(5-4)中a(d,Ti)是统计在Ti时刻该dT-I识别域内仍存活的异常事件数量。
式(5-4)中k(Ti)为激励函数,模型以SN(di)的识别域为交叉激励的邻域,所谓的激励是指在Ti时刻SN(di)中所有存活异常模式的总数量影响当前受到刺激dT-I的被激活概率,也就是说SN(di)中某一检测器在Ti时刻捕获的异常模式可能与域内其他的检测器中仍存活的异常模式存在关联,通过调节k(Ti)来实现这种关联的强弱。激励函数定义如下:

图5-5 检测器与异常事件的生命周期图(https://www.daowen.com)
![]()
式中:β为激励系数,调节激励的强度;A(Ti)是在Ti时刻SN(di)中所有存活异常模式的总数量,随着A(Ti)-a(d,Ti)的增加激励强度放缓,便于其他的检测器在也有活化的机会。当β=0.768时,k(Ti)的激励曲线如图5-6所示。

图5-6 初始检测器群的激励曲线k(Ti)
图5-6中,A(Ti)-a(d,Ti)=20时,激励强度达到最大,即k(Ti)=2,则检测器的活化概率也增大,概率曲线的变化如图5-7所示。
图5-7显示受邻域异常模式激励的检测器,其被激活的机会增加。为了实现上述机制,检测器集SN(di)需要每一个时间步中维持以下的信息:
(1)SN(di)。生命周期减一,当T-I=0时,SN(di)被清除。
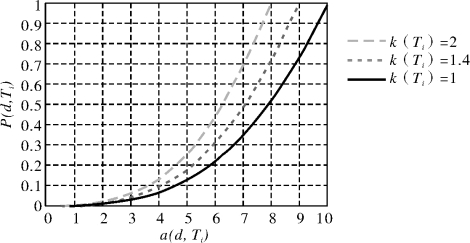
图5-7 受邻域激励的检测器活化概率变化曲线
(2)ab。生命周期减一,当tab=0时,删除。
(3)A(Ti)。统计当前SN(di)中所有ab的数量。
(4)a(d,Ti)。统计当前每一个检测器中的ab的数量。
