4.4.1　聚类算法

4.4.1　聚类算法

4.4.1.1　 K-means聚类算法

K-means聚类算法（K均值聚类算法）是一种基于划分的聚类算法，它尝试找出使聚类性能指标最小化的k个划分，通常使用的聚类性能指标函数是聚类集中的每个数据或对象到该类中心的聚类平方之和，并使它最小化：

（1）设定聚类数k。

（2）让C1，…，Ck，为初始类中心，将数据集划分为k数，使所有样本xi隶属于某一类Cj，即没有任何数据点隶属于2类或多类。引入一组D维向量μk，其中k=1，…，k，且μk是与第k个聚类关联的均值向量（质心）

（3）K-means算法的目标是找到数据点分别属于的聚类，以及一组向量使得每个数据点和与它最近的向量μk之间的距离的平方和最小即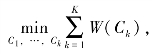其中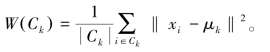

（4）K-means算法基本流程是先将簇初始化为Ck=∅，（t=1，2，…，k），计算样本xi和各个质心向量μk的距离：dik=‖xi-μk‖2，将xi标记最小的为dik所对应的类别λi，此时更新Cλi=Cλi∪{xi}。再重新计算每个质心如果所有的K个质心向量都没有发生变化或达到最大迭代次数N则输出簇划分

K-means算法的优点为：

（1）对处理大数据集，K-means算法是相对可伸缩的和高效率的，因为它的计算复杂度为O（nkt），其中n为对象个数，k为聚类个数，t为迭代次数，通常有k≪n和t≪n。

（2）空间复杂度是O（k＋n），如果可以把所有的数据储存在内存里，存取所有元素则非常快，因此，效率非常高。

（3）不依赖于顺序。给定一个初始类分布，无论样本算法的顺序如何，分区过程结束后生成的数据分区都一样。

K-means算法的缺点为：

（1）生成的聚类数是要预先给定的，不能动态添加新的聚类。

（2）对噪声和异常点很敏感，即使是少数这样的数据对平均值的影响也很大。

（3）需要给出类平均值，因此它不适合处理有分类属性的数据。

由于网络行为十分复杂，其正常模式集的样本空间分布可能呈任意形状，如采用K-means聚类算法会对自我空间S边界的界定产生较大的误差，严重降低候选检测器集产生的有效性和可靠性；另一方面随着网络环境的变化或时间的迁移，正常模式集会有较大的变动，而K-means聚类算法不具备增量式动态更新的特点，需要更新整个样本空间，而Strn的尺寸巨大，其时间开销很大。

4.4.1.2　 DBSCAN聚类算法

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）是具有噪声的基于密度的聚类方法。其基本思想是：对于一个聚类中的每一个对象，在其给定半径ε的邻域中包含的对象不能少于某一给定的最小数目（MinPts），然后对具有密度连接特性的对象进行聚类。在该算法中，发现一个聚类的过程是基于这样的事实：一个聚类能够被其中的任意一个核心对象所确定。假设样本集是则DBSCAN具体的密度描述定义如下：

（1）ε-邻域。对于xj∈D，其ε-邻域包含样本集D中与xj的距离不大于ε的子样本集，即Nε（xj）={xi∈D｜distance（xi，xj）≤ε}，这个子样本集的个数记为｜Nε（xj）｜。

（2）核心对象。对于任一样本xj∈D，如果其ε-邻域对应的Nε（xj）至少包含MinPts个样本，即如果｜Nε（xj）｜≥MinPts，则xj是核心对象。

（3）密度直达。如果xi位于xj的ε-邻域中，且xj是核心对象，则称xi由xj密度直达。注意反之不一定成立，即此时不能说xj由xi密度直达，除非且xi也是核心对象。

（4）密度可达。对于xi和xj，如果存在样本序列p1，p2，…，pT，满足p1=xi，pT=xj，且pT＋1由pT密度直达，则称xj由xi密度可达。也就是说，密度可达满足传递性。此时序列中的传递样本p1，p2，…，pT-1均为核心对象，因为只有核心对象才能使其他样本密度直达。密度可达也不满足对称性，这个可以由密度直达的不对称性得出。

（5）密度相连。对于xi和xj，如果存在核心对象样本xk，使xi和xj均由xk密度可达，则称xi和xj密度相连。密度相连关系是满足对称性的。

DBSCAN聚类算法的基本流程：针对样本集D设置邻域参数（ε，MinPts），初始化核心对象集合Ω=∅，初始化聚类簇数k=0，初始化未访问样本集合Γ=D，簇划分C=∅，对于j=1，2，…，n，按下面的步骤找出所有的核心对象：①通过距离度量方式，找到样本xj的ε-邻域子样本集Nε（xj），②如果子样本集样本个数满足｜Nε（xj）｜≥MinPts，将样本xj加入核心对象样本集合Ω=Ω∪{xj}；在核心对象集合Ω中，随机选择一个核心对象o，初始化当前簇核心对象队列Ωcur={o}，初始化类别序号k=k＋1，初始化当前簇样本集合Ck={o}，更新未访问样本集合Γ=Γ-{o}；当前聚类簇Ck生成完毕，更新簇划分更新核心对象集合Ω=Ω-Ck；在当前簇核心对象队列Ωcur中取出一个核心对象o′，通过邻域距离阈值ε找出所有的ε-邻域子样本集Nε（o′），令Δ=Nε（o′）∩Γ，更新当前簇样本集合Ck=Ck∪Δ，更新未访问样本集合Γ=Γ-Δ，更新Ωcur=Ωcur∪[Nε（o′）∩Ω]。

DBSCAN算法的优点是可以挖掘任意形状的聚类，对数据输入顺序不敏感，并且具有处理异常数据（噪音）的能力。由于它是根据一个密度阈值来控制类的增长，DBSCAN算法具备增量式动态更新的特点。其缺点是该算法的效率低，时间复杂性为O（n×n）；在空间索引如k-d树的支持下，其复杂性为O（n×logn），需要指出的是，DBSCAN算法没有考虑建立索引的时间，而建立索引通常需要消耗大量的时间，严重影响网络入侵检测系统的性能。

4.4.1.3　 CLIQUE聚类算法

CLIQUE（clustering In QUEst）聚类算法是采用一个多分辨率的网格数据结构，把对象空间量化为有限数目的单元，形成了一个网格结构。所有的聚类操作都在这个网格结构上进行。其核心思想是：首先扫描所有网格。当发现第一个密集网格时，便以该网格开始扩展，扩展原则是若一个网格与已知密集区域内的网格邻接并且其自身也是密集的，则将该网格加入到该密集区域中，直到不再有这样的网格被发现为止。（密集网格合并）算法再继续扫描网格并重复上述过程，直到所有网格被遍历。以自动地发现最高维的子空间，高密度聚类存在于这些子空间中，并且对元组的输入顺序不敏感，无须假设任何规范的数据分布，它随输入数据的大小线性地扩展，当数据的维数增加时具有良好的可伸缩性。

定义k维空间S=V1×V2×…×Vk为有界定义域，其中Vi是空间S第i维（属性、字段），算法的输入是一个k维空间中的点集其中的第j个分量通过输入一个参数ε，可以将空间S的每一维分成相同的ε个区间，从而将整个空间分成有限个不相交的类矩形单元，每一个这样的矩形单元可以描述为其中是一个前闭、后开的区间。一个xi落入区间ui当且仅当对于定义一个单元格u的选择率selectivity（u）=单元格中点的个数/数据空间中总的点个数。对应输入参数τ，称数据单元u是密集的，当且仅当selectivity（u）＞τ。聚类可以定义为在k维空间中由一些连通的密集单元格组成的连通分支。两个k维中的单元格ui、uj称为连通的当且仅当这两个单元格有一个公共的面，或ui、uj都跟另一个单元格um连通。两个单元格有一个公共的面则存在一个k-1个维度有成立（t=1，2，…，k-1），并且对于第k维有或者成立。CLIQUE聚类步骤如下：

（1）对n维空间进行划分，对每一个维度等量划分，将全空间划分为互不相交的矩形单元，并且识别其中的密集单元。

CLIQUE采用自底向上的识别方法，利用关于维度的聚类准则的单调性来修剪搜索空间。该算法与用于挖掘关联规则的Apriori算法（先天算法）相似。单调性是指如果点集S是k维空间中的一个聚类，则S也是该空间的任何（k-1）维投影中的聚类的一部分。

首先确定低维空间的数据密集单元，当确定了k-1维中所有的密集单元，k维空间上的可能密集单元就可以确定。因为，当某一单元的数据在k维空间中是密集的，那么在任一k-1维空间中都是密集的。如果数据在某一k-1维空间中不密集，那么数据在k维空间中也是不密集。由k-1维的密集单元格集合Ck-1生成k维的候选密集单元格集合Ck，候选集合生成算法G如下：

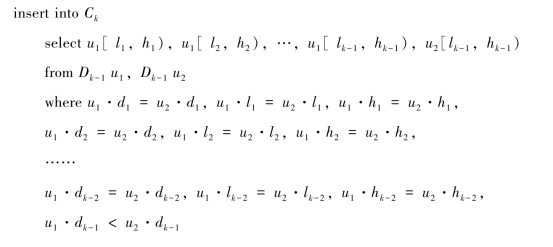
其中，Dk-1是k-1维密集单元集，u1.dk表示u1单元的第k维。算法的缺点在于可能产生大量候选集，并且会频繁使用数据点。虽然这种算法减少了需要验证的密集单元个数，但随着维数的增加，这个数量级依然很大。时间复杂度分析：如果密集单元存在于k维中，则k维子集中的所有投影O（2k）个不同的组合也是密集的。因此算法的运行时间是任何密集单元的最高维数的指数。算法G过程产生的候选数量最少，可以保证找到所有密集单元。令k是任何密集单位的最高维数，m是输入点的数量，算法运行时间为O（ck＋mk），其中c是一个常数。

（2）CLIQUE采用了基于“覆盖”的修剪原则来对子空间进行修剪。利用MDL（Minimum Description Length）原理，对候选集进行剪枝。MDL基本原理是如果k维空间存在一个聚类，那么k维空间的所有子空间都应该包含聚类的所有点。所以对k维空间的所有子空间从大到小进行排序，然后剪枝，在给定MDL模型下对输入数据进行编码，并选择使代码长度最小化的编码。

假设密集子空间为S1，S2，…，Sn，修剪技术首先将位于同一子空间中的密集单元组合在一起，对于每个子空间，它计算数据集中由密集单元覆盖的部分：表示一个子空间Sj中所有稠密单元内数据点的个数。选择具有大覆盖的子空间，并对其余空间进行修剪，理由是如果在k维中存在簇，那么对于这些k维的每个子空间，在该子空间中存在密集单元（覆盖在原始k维中的簇的密集单元的投影），其至少覆盖簇中的点。按照其覆盖的降序对子空间进行排序，把子空间的排序列表分成两组：选择集I和修剪集P。对于每个集合，计算覆盖分数的平均值，并且对于该集合中的每个子空间，计算与平均值的差值，代码长度是存储的位数的长度之和。如果决定修剪子空间Si＋1，…，Sn，平均值：uI（i）=则log2[uI（i）]和log2[uP（i）]计算平均值uI（i）和uP（i）的位数，子空间的编码总长度为：

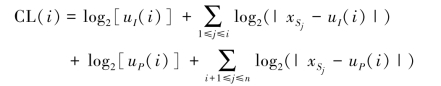
最小化CL（i以确定最佳切割点i值，即剪枝点：留下剪枝点左边的，去掉剪枝点右边的），如图4-2所示。

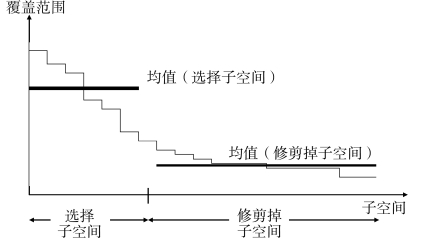
图4-2　子空间修剪

（3）识别聚类。利用DFS（Deep First Search）来发现空间中的聚类。即从D中一个密集单元u开始，按照深度优先遍历的原则，查找连通的集合。图顶点对应于密集单元，并且当且仅当对应的稠密单元具有公共面时，在两个顶点之间存在边缘。在图的同一连通分量中，对应于顶点的单元是连通的，因为在它们之间有一个具有共同面的单元的路径，因此它们在同一个簇中。另一方面，对应于不同连通分量中的顶点的单元不能连接，因此不能在同一个簇中。使用深度优先搜索算法来找到图的连通分量。从D中的某个单元开始，给它分配第一个簇号，并找到它所连接的所有单元。然后，如果D中仍然有尚未访问的单元，找到一个并重复该过程。算法描述如下：

（4）为每个簇生成最小化描述。k维的区域是一个轴平行的矩形k维集合，每个簇需确定覆盖相连的密集单元的最大区域，再确定最小的覆盖区域。最大区域是指区域R包含于一个聚类C，当且仅当R∩C=R，并且不存在R的超集R也包含于C。图4-3显示了2维空间（age，salary）分为10×10的单元格。

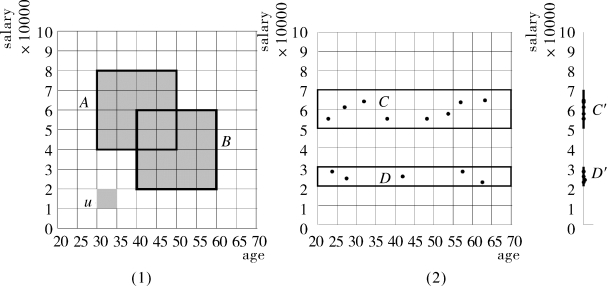
图4-3　原始数据空间的子空间（投影）中识别簇

图4-3（1）中u=（30≤age＜35）∧（1≤salary＜2），A和B是由多个u组成的矩形区域。假设阴影单元是密集的，A∪B是一个簇，A是包含在该簇中的最大区域，而A∩B不是最大区域，簇最小化描述：[（30≤age＜50）∧（4≤salary＜8）]∨[（40≤age＜60）∧（2≤salary＜6）]。

图4-3（2）中假设τ=20%，没有2维密集单元且原始数据空间中没有簇。但是，如果点数投影在salary维度上，则有三个1维密集单元。其中两个是连接的，所以在1维salary子空间中有两个簇：C′=5≤salary＜7，D′=2≤salary＜3。age子空间中由于没有密集单元则没有类。

利用贪心算法找到覆盖每个子聚类的最大区域覆盖，然后再确定最小覆盖区域是指每一边都与坐标轴平行的类矩形。首先选择一个密集单元，找到包含该密集单元的最大区域，然后再选择该聚类中没有包含在已有最大区域中的密集单元，找到包含密集单元的最大区域，知道所有密集单元都包含在最大区域集中。因为最大区域集中存在重叠的子空间，所以根据最大区域集，来确定最小覆盖。

贪心算法：从任意密集单元u1∈C开始，贪心地生长覆盖u1的最大区域R1。将R1加入到R中，然后找另一个u2∈C还没有被R中的任何最大区域覆盖，贪心地生长覆盖u2的最大区域R2。重复这个过程，直到C中的所有单位被R中的某个最大区域覆盖为止。

为了获得覆盖密集单元u的最大区域，从u开始并沿着维度d1，将其生长到单元的左侧和右侧。根据C中所包含的连接密集单元在两个方向上尽可能多地覆盖u，产生结果是矩形区域，然后沿着该区域的维度d2上继续生长这个区域。再次从C中取连接的密集单元，以获得可能较大的矩形区域。对于所有的维度重复这个过程，产生一个覆盖u的最大区域。

图4-4说明了算法原理，密集的单位出现阴影。从密集单元u开始，首先沿着水平维度生长，发现矩形A由4个密集单元组成。然后在垂直维度上扩展A。当它不能被进一步扩展时，得到最大矩形，在这种情况下，下一步是寻找另一个最大区域，该区域从没有被B覆盖的密集单元开始，例如W。

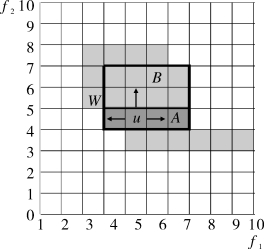
图4-4　贪心增长算法示意

时间复杂度分析：对于每个最大区域R，贪心算法必须完成是区域R中密集单元的数量）数量级的密集单元的访问。设S是R中的子空间，包含一个具有n个密集单元的簇，由两个平行超平面和一个平行于一个维度的圆柱组成。由于超平面不平行于任何k维，所以碰到超平面的簇的边界由O（n（k-1）/k）个凸顶点组成，每个顶点必须被最大区域覆盖。因为每个区域必须到达另一个超平面，则区域的大小也是O（n（k-1）/k）。在这种情况下，贪心算法必须执行O（n（k-1）/k）密集单元访问。

CLIQUE聚类算法的主要优点是它的处理速度很快，其处理时间独立于数据对象的数目，只与量化空间中每一维的单元数目有关。同时CLIQUE聚类算法拥有DBSCAN的多个优点，如能挖掘任意形状的聚类、对数据输入顺序不敏感、处理异常数据（噪音）的能力等，同时还具有算法效率高的优点以及可以处理高维的数据等特点。不过它用一个网格内的统计信息来代替该网格内的所有点，会导致聚类质量的下降。