4.7.2 增量式动态更新算法
由于时间因素而导致自我空间的不完整描述，进而增加e＋，因此需要动态更新加以修正。由上节的分析可知，新增加的自我模式对自我空间的影响体现在自我空间的边界上，对其主体结构的影响不大，因此更新是各个子类空间的边界拓延。然而针对新增样本的加入，传统的聚类方法需要更新整个样本空间，由于训练集本身的尺寸巨大，其时间开销很大，对于IDS是不现实的，因此必须采用增量式动态的更新方式。
结合MBNSA算法的特点，本节讨论针对时间因素的更新策略。假设新增自我模式集Enew映射到模式空间U中，引发部分单元空间c的密度变化为m′（c），会出现4种不同的情况，相应的更新策略如下：
（1）ifm（c）≥δlow，m′（c）＞δlow：记录密度的变化。
（2）ifm（c）＜δlow，m′（c）≥δlow且near（c）≠∅：记录密度的变化，将c并入相应的自我子空间，MBNSA算法更新检测器集。
（3）ifm（c）＜δlow，m′（c）≥δlow且near（c）=∅：记录密度的变化。
（4）ifm（c）＜δlow，m′（c）＜δlow：记录密度的变化。
可见只有当新增的模式影响到网格密度发生如情况（2）的变化时，MBNSA算法才会工作，在（3）和（4）的情况下，新增模式被视为噪声或异常数据而被忽视，也就是说只有当曾被遗漏的自我模式在更新期内频繁出现且发生在某一自我子空间的边界上时，才会引发自我空间的更新。
MBNSA算法的特点，可以从正反两个方面来考虑：其不利的一面是修正e＋的效果有所下降；其有利的一面是，排除了偶然事件对有效检测器的影响，同时使得入侵者企图诱导训练模型的恶意行为变得更加困难，这体现了MBNSA算法的鲁棒性。通过降低密度阈值δlow可以提升修正e＋的效果不，但如前所述这样会导致e-的增加，因此需要均衡考虑。
MBNSA算法采用网格密度来界定检测器的有效性，实际上已具备了增量式动态更新的特点，即一个空间单元在更新后仍保持其密度属性，将不会对MBNSA算法产生任何影响，因此只需考虑那些密度属性发生变化的单元。这里提出了一种基于MBNSA的增量式动态更新算法IMBNSA（Incremental Algorithm of MBNSA）来解决自我空间的不完整问题，下面给出具体的实现。
设原有的训练集为Etrn，新增自我模式集为Enew，则更新后E′trn=Etrn∪Enew。让Δs表示新的模式插入，一个空间单元c中如至少有一个点被插入，即表示该单元被更新，因为插入行为只是影响该单元的密度，所以我们只是关心单元的更新状况而不必考虑单个数据的更新，更新后的密度为m′（c）。
定义密度属性发生变化的单元集合为
且c∉Cself}，原有的自我集合为Cself，则更新后C′self=Cself∪ΔCself。IMBNSA算法描述如下：
在表4-7的基础上，将上节Echeck中10000个记录作为新增自我模式集，归一化处理后映射到模式空间中，有119个单元的密度属性发生变化即｜ΔCself｜=129，采用算法IMBNSA更新各个子空间，更新结果如表4-8。
表4-8 各个子空间的更新结果
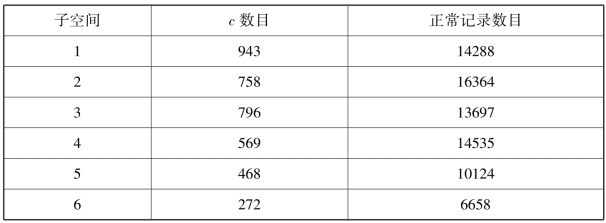
自我空间新增127个c，其中ΔCself中有101个c被归入子类空间（其余18个c为孤立点），另外26个c是在未更新前的孤立点而新更新后它们的near（c）≠∅则被归类，大约占总正常记录集2.08%的数据被滤掉。自我空间得到更新，进一步趋于完整。
算法IMBNSA增量式地动态更新发生变化的局部样本空间，使入侵检测系统能迅速适应网络环境的变化。而针对网络结构的变迁，网络服务的增减、网络行为的方式或习惯的改变等原因造成正常网络行为模式的剧烈变化，导致最小有效候选检测器集的覆盖域发生较大范围的迁移，则有必要更新整个样本空间。