5.2.2 反向判定规则集的遗传算法GAND
在IAIDM模型中自我模式在模式空间U中只占有很小的一部分区域，由定义4.5将模式空间的绝大部分区域划为非我空间N，但实际上在非我空间N中每一点不可能都是入侵的特征模式点，也就是说非我模式和自我模式一样不是随机分布在模式空间中任何一处，而是聚集分布在模式空间中的某几个区域内，也只是占据U中很小的一部分区域，不同的是非我模式分布的时间和空间未知而已。如前所述，典型的入侵行动会影响10～20个审计记录，而这些审计记录即是非我的模式，所谓的异常呈现就是在第一时间内将这些异常的记录呈现出来，并触发初始检测器的产生。
在本模型中采用一个空间网格c内的统计信息来代替该网格内的所有点，即一个网络行为模式x∈c，如果c⊂N，则异常；如果c⊂S，则正常；因此鉴别一个网络行为是否异常有两种方式：正向判定PD（Positive Distinguish）和反向判定ND（Negative Distinguish）。
PD是将网络行为模式x映射到模式空间U中，计算其所属单元空间的信息，即
将其映射到索引空间A中，借鉴MBNSA算法的第7步，首先检查该点是否落在某一
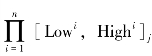中，否则判定为异常；是则进一步检查该点是不是属于该Aj，是则判定正常，否则判定为异常，PD的时间复杂度计算见小节4.5.1，免疫模型为了及时发觉异常行为，需要实时审核监视网络事件，而通常情况下入侵事件只占到整个网络事件的很少一部分，如果自我空间的结构紧凑简单，正向判定不失为一种方便的方法，但网络的环境通常比较复杂，其自我空间的分布较广且复杂，采用正向判定时系统开销较大，无法在第一时间内呈现异常事件。
ND是首先将非我空间N划分为多个大小不等的空间矩阵集合，划分的标准是在不与集合Cself相交的前提下其覆盖的区域尽可能的大。空间矩阵集合确定后，检验某一网络行为模式是否落在该空间矩阵集合内，是则判定为异常并呈现出来，否则判定为正常。设空间矩阵集合B={B1，…，Bm}，非我空间N=B1∪B2∪…∪Bm且Bi∩S=∅，检验的规则为：
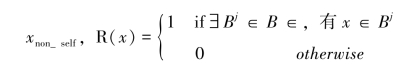
其中
（x1，…，xn）是模式x在各维坐标轴上的特征分量
1.0]（j=1，2，…n）规定了空间矩阵Bi在各维方向上的上边和下边，n为空间维数。
ND的时间复杂度为O（｜B｜）。由公式（4-5）和（4-6）可知，｜Cself｜对ε很敏感，即使ε发生较小的变化，｜Cself｜成指数增长，则PD的时间复杂度也会随之成指数增长，而｜B｜只与整个自我空间分布情况有一定的关系如分布的规则性和子空间数等，与｜Cself｜无关，即使较大的变化ε，｜B｜只会在一定范围内发生较小的波动，因此有O（｜B｜）≪O[m＋max（｜A1｜，｜A2｜，…，｜Am｜）]，另外不必每次都要计算x所属单元空间的信息c：
以及空间的转换，所以ND的判定速度很快，同时集合B还有加速入侵模式被相应检测器识别的功能，我们将在后面具体分析。例如空间维数为2，空间矩阵Bi的划分如图5-2所示，Bi之间可以部分相互覆盖。
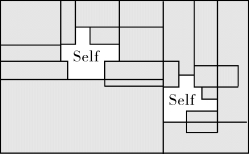
图5-2 非我空间N的矩阵空间划分
Self表示自我空间，Self外的空间用矩阵覆盖
由于Self是基于网格密度形成的，所以其边界不是任意的形状
这里我们将空间矩阵集合B称为反向判断规则集B，其可以视为通用的、非专门化的检测异常行为的检测器，执行功能类似于免疫系统中的T细胞。采用遗传算法来进化空间矩阵集合B来覆盖非我空间N，遗传算法的进化目标是在不与集合Cself相交的前提下使Bi尽可能的覆盖更多的区域。Bi的划分受到三个因素的约束：①Bi内包含c∈Cself的数量；②Bi覆盖的面积；③Bi间的交叠面积。
很明显这是一个多模多目标的优化问题。遗传算法中的每一个个体（染色体）代表Bi在各维方向上的上边和下边，染色体的组成为：low1，…，lown；high1，…，highn。由前所述，模型将模式空间U网格化，并将各个空间单元的位置信息
映射到整数索引空间A：[0，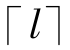
-1]n中，包括了Cself中的各单元，即自我点集Aj（j=1，…，m），同样B在各维方向上的
映射到空间A，则lowj和highj取区间[0，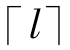
-1]内的整数，约束条件（1）转为包含点a∈Aj的数量。染色体中的各段用固定长度的二进制串表示，通过计算（highj＋1）×h或（lowj＋1）×h将二进制串转换到区间[0.0，1.0]中，其中h为间隔宽度。我们称集合B生成算法为反向判定规则集的遗传算法GAND（Genetic Algorithm of ND），具体描述如下：
适应度评价：
其中V（Bi）为Bi的空间体积：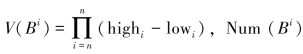
为Bi包含自我点的数量：Num（Bi）={aj∈R｜aj∈Bi}；P为惩罚系数，P越大，惩罚力度越大。算法中Cover（b，Bi）是用于约束条件3，降低覆盖域的交叠，定义如下：
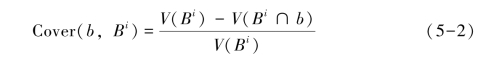
在小节4.6.1的实验中，当ε=0.005及δlow=10时，采用MBNSA算法对E1进行处理，共产生10个子空间区域，如表4-4所示。我们将其中6个自我子空间映射到空间A中，形成自我点集Aj（j=1，…，6）作为算法GAND的输入，间隔宽度
有l=316.27，则lowj和highj取区间[0，316]，染色体的长度设为16bit，相关参数设定：T=2000，f=200，Pm=0.1，P=1.0。运行10次，实验结果见表5-1。
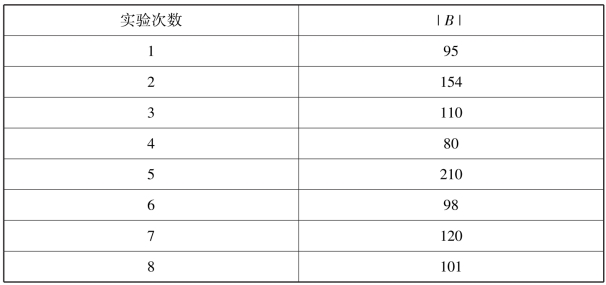
表5-1 算法GANS的实验结果
续 表
反向判定规则集B的大小平均为116.3，表4-4中子空间1、4和6的投影空间发生重叠，因此PS需要扫描比较的最大样本数为2867，消耗的时间比ND高出约25倍，随着ε减小，这个比例会非线性扩大。实验评估PD和ND的判别性能，我们从评估数据集中随机抽出5000个事件记录对象，其中正常连接记录4500个，入侵记录500个，进行10次实验并取其平均结果，则PD和ND的正确判别率TD（Ture Distinguish）和运行时间t结果见表5-2。
表5-2 PD和ND的TD和t
表5-2实验结果表明PD虽然效率较低，但其正确判别率TD较ND的高，这是由于算法GAND输出的反向判定规则集B可能未能完全覆盖N或与集合Cself有相交的部分。均衡考虑两种算法的精度和效率，本模型拟采用反向判定ND作为异常呈现算法以适应入侵检测系统实时性的要求。