4.7.1 非完备性分析
由于免疫模型训练期时间的限制,遗漏了部分自我模式的收集,导致自我空间的描述不完整,这里引入离散随机过程的分析方法来估计e+发生概率。
训练期间,模型收集的自我模式数据集为Etrn,而检验期间出现的自我模式数据集为Echeck。假设所有的自我模式x皆由随机过程X产生,x定义为一组随机变量![]() 同时假设所有随机变量在整个时间段内都服从相同的分布,即:
同时假设所有随机变量在整个时间段内都服从相同的分布,即:
![]()
在这段时间内同一模式可能出现多次,模型中自我模式是多维的实向量,为了简化统计分析的复杂性,结合IAIDM用空间网格内的样本统计信息来代替该网格内所有点,即落在同一空间网格c内的样本点具有很高相似度的特性,将落在同一空间网格c内的所有自我模式x视为是同一模式,记为c。同样假设所有的c由随机过程Q产生,c定义为一组随机变量![]() 且在整个时间段内都服从相同的分布,即:P(Qi=c)=P(Qj=c)=p(c)(i,j=1,2,…),训练集
且在整个时间段内都服从相同的分布,即:P(Qi=c)=P(Qj=c)=p(c)(i,j=1,2,…),训练集![]() 并以网格密度m(c)作为c出现的频率。因此根据Q的输出可以定义一个样本分布
并以网格密度m(c)作为c出现的频率。因此根据Q的输出可以定义一个样本分布![]() 假设其样本分布近似于实际分布
假设其样本分布近似于实际分布![]() 设训练集Etrn的收集时间为t=1到t=T,在训练期收集的唯一的自我模式集为
设训练集Etrn的收集时间为t=1到t=T,在训练期收集的唯一的自我模式集为![]() 其中g(T)=|Etrn|。设模型的检测期为t=T+1到t=∞,即
其中g(T)=|Etrn|。设模型的检测期为t=T+1到t=∞,即![]() 其间出现的唯一自我模式集为
其间出现的唯一自我模式集为![]() 其中g(∞)=|Echeck|+g(T)。
其中g(∞)=|Echeck|+g(T)。
在最坏的情况下,Echeck中的所有模式皆未在训练期间出现过,即ct∈Echeck,但ct∉Etrn,其中t=g(T)+1,g(T)+2,…,g(∞)。给定随机过程Q的样本分布![]() 第一次出现的概率服从以P˜(ct)为参数的几何分布,即:
第一次出现的概率服从以P˜(ct)为参数的几何分布,即:
![]()
那么ct是一个e+的概率为:
![]()
则检测期内发生e+的概率为:
![]()
若ct的产生相互独立,则有:
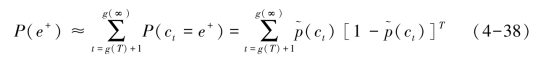
用泰勒级数展开式(4-38)得:
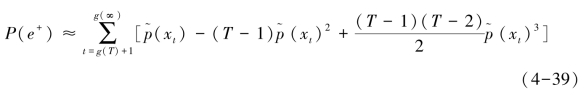
当T足够大时,T-2≈T-1≈T,有:(https://www.daowen.com)
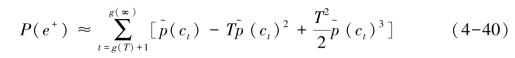
若随机过程的随机变量都服从相同的分布,且训练集的样本分布近似于其实际分布,在给定训练时间和训练集的情况下,式(4-40)可以用来估计e+发生概率。
在小节4.5.2中实验数据集E包含67278个正常记录,这里用作训练集Etrn,另外从评估数据集中随机取10000个记录用作自我检验集Echeck。这里暂不考虑噪声或孤立点的问题,将Etrn中的每一个点归一化处理后映射到模式空间中,则训练期中唯一的自我模式集变为![]() 其中g(T)为出现频率高于0的c数量,即g(T)=|Cne|。检测期间,将Echeck中的每一个点归一化处理后映射到模式空间中,会影响到原有c的m(c)发生变化,有以下两种情况:
其中g(T)为出现频率高于0的c数量,即g(T)=|Cne|。检测期间,将Echeck中的每一个点归一化处理后映射到模式空间中,会影响到原有c的m(c)发生变化,有以下两种情况:
(1)ifm(c)>0,m′(c)>0:该自我模式c曾出现在Etrn中;
(2)ifm(c)=0,m′(c)>0:该自我模式c未出现在Etrn中。
则![]()
当ε=0.005时,Etrn和Echeck经过上述转换后,Etrn中共有唯一的模式3969个。Echeck中共有唯一的模式1561。比较Etrn和Echeck,Echeck中有73个模式没有出现在Etrn中,则唯一自我模式集E的总数为4042,其中最低的发生概率为1.294×10-5{min[m(c)]/77278,min[m(c)]=1},而最高的发生概率为![]() 有281个c的出现频度较高[m(c)>89],它们包含的样本点数占总样本数的91.32%,其余3761个则占样本总数的8.68%,图4-8给出了样本分布的逻辑图。
有281个c的出现频度较高[m(c)>89],它们包含的样本点数占总样本数的91.32%,其余3761个则占样本总数的8.68%,图4-8给出了样本分布的逻辑图。
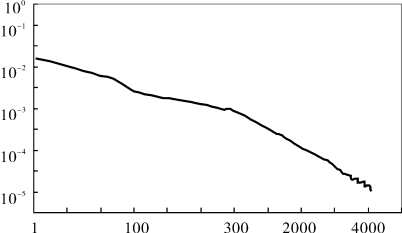
图4-8 c样本分布的逻辑图
样本的出现频度经归一化处理来表示样本产生概率
较高频度出现的c形成各个子类空间的中心区域,即样本密集分布区,而低频出现的自我模式c通常散布在各个中心区域的周围,也就是说训练集的非完备性问题对自我空间的影响主要体现在自我空间的边界上,即低频出现的自我模式才会导致e+。所以针对训练集非完备性的问题,实验中只需要分析上述3761个出现频度相对较低的c发生概率,按出现的频度,将c从大到小排序,可以用一个静态的指数过程较精确的描述其分布,即p(ci)=ai-b描述,其中a=16.11,b=1.69,i∈[282,4042]。用c的实际分布p(ci)代入式(4-40),替换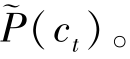

由上可知g(T)=3969,g(∞)=3969+1561=5530,Etrn中有模式67278个,即T=67278,则P(e+)≈0.0096。模型检测到所有Echeck中的自我模式,则有e+≈0.0096×10000≈96,即误检错误为96次。Etest中有73个模式没有出现在Etrn中,式(4-40)估计的误检错误比实际结果要高些。由于模型训练中,训练集Etrn中少量c是孤立点[near(c)=∅且m(c)≥δlow]或其出现频率小于δlow而作为噪声被滤掉,因此实际的e+发生概率要接近于或高于式(4-40)的估计值。
随着检测周期的延长,出现的自我模式越来越多,发生误检错误的次数也随之增多,使模型的有效性下降,因此有必要对模型的自我空间进行不定期的更新,保持检测器集的有效性。
