4.4.2 降维算法
AIS中抗体被定义为检测器，抗原代表输入样本空间中的特征向量，训练成熟的人工免疫检测器被用于对非自体抗原（即采集到的异常样本特征）进行检测与识别，因此，免疫检测器的性能决定了AIS检测结果的准确性和有效性，然而高维空间下检测器超球体的覆盖体积将迅速减少，在高维度特征空间下，覆盖同样体积的非自体空间需要的检测器数量将随样本维数的增加呈指数氏增长，同时如上分析自我空间的聚类算法如CLIQUE的时间复杂度与样本维数呈指数增长。数据降维有利于有效信息的提取及无用信息的摈弃，降低计算复杂度。
数据降维主要是通过线性/非线性的方式将原来高维空间变换到一个新的空间。一种是基于从高维空间映射到低维空间的投射方法，其中代表算法就是PCA、LDA、自编码等，主要目的就是学习或者算出一个矩阵变换A，用这个矩阵与高维数据相乘得到低维数据。另一种是基于流形学习的方法，流形学习的目的是找到高维空间样本的低维描述，它假设在高维空间中数据会呈现一种有规律的低维流形排列，但是这种规律排列不能直接通过高维空间的欧氏距离来衡量，如果能够有方法将高维空间中流形描述出来，那么在降维的过程中就能够保留这种空间关系。为了解决这个问题，流形学习假设高维空间的局部区域仍然具有欧氏空间的性质，即它们的距离可以通过欧氏距离算出（Isomap），或者某点坐标能够由临近的节点线性组合算出（LLE），从而可以获得高维空间的一种关系。而这种关系能够在低维空间中保留下来，从而基于这种关系表示来进行降维，因此流形学习可以用来压缩数据、可视化、获取有效的距离矩阵等。线性映射方法的代表方法有：PCA、LDA等，而非线性映射方法的代表方法有：KPAC、t-SNE、ISOMap、LLE、LPP、LE等。
4.4.2.1 1PCA
主分量分析PCA（Principal Component Analysis）由卡尔·皮尔逊在1901年发明，是一种线性降维方法。高维空间（维数为D）的某个点xi=（x1，x2，…，xD）通过与矩阵A相乘映射到低维空间M中的某个点yi=ATxi，其中A的大小是D×M，得到N个从D维空间映射到M维空间的点。PCA的目标是让映射得到的点{yi}尽可能的分开，即{yi}的方差尽可能大，方差是{yi}协方差矩阵的轨迹：
其中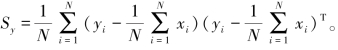
设Sx是{xi}的协方差矩阵，由于tr（Sy）=tr（ASxAT），使用拉格朗日乘数并取导数得到：
其中uk是Sx特征向量，则：
取M个最大特征值λk的特征向量uk，计算xi的估计值：
4.4.2.2 LDA
线性判别分析LDA（Linear Discriminant Analysis）是一种监督学习的降维技术，也就是说它的数据集的每个样本是有类别输出的。LDA的思想是投影后类内方差最小，类间方差最大。
设数据集有k个类，每个类有Nj个节点，每个类的均值节点为uj，所有节点的均值节点为u，则计算类间散度矩阵：
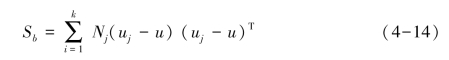
类内散度矩阵：
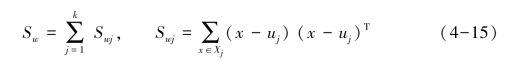
其中Xj为第j类样本的集合。
目标函数：
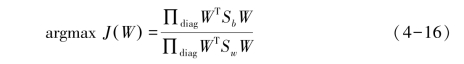
其中∏diagA是A的主对角线元素的乘积，W为m×d的矩阵。投影矩阵W：计算
取最大的M个特征值和对应的M个特征向量得到投影矩阵W，于是
4.4.2.3 KPCA和KECA
在实际应用中，样本特征间往往呈现出较为复杂的非线性关系，在线性子空间中不能很好地表示，核成分分析法KPCA（Kernel PCA）PCA推广到非线性降维。
对于线性不可分的数据集，可以将其映射到高维上，再进行划分。假设非线性变换Φ（x）将原始D维特征空间变换到M高维特征空间（M≫D）。每个数据点xi被投影到新的特征空间中的点Φ（xi）且均值为0：
投影特征的协方差矩阵：
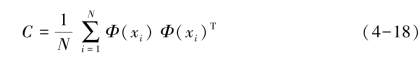
C的特征值和特征向量：
其中k=1，2，…，N。由公式（4-18）和（4-19）得：
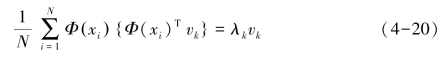
由定理：空间中任一向量（包括基向量），都可以由空间中的所有样本线性表示，将特征向量vk利用样本集合Φ（xi）线性表示：
由公式（4-20）和（4-21）得：
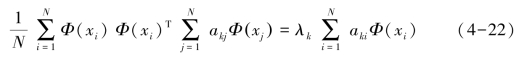
定义核函数如下：
公式（4-22）两边乘以Φ（xi）T有：
公式（4-24）用矩阵表示：K2ak=λkN Kak，其中ak=[ak1，ak2，…，akN]T可以由下式解得：
可以计算得到的核主成分如下：
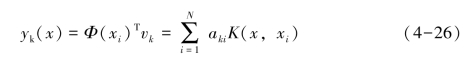
KPCA以数据服从正态分布为前提，以特征值大小作为所携带信息量的评价指标，因此，KPCA所选择的降维投影方向可能并不是对分类信息贡献率最大的投影方向。
核熵成分分析法KECA（Kernel Entropy Component Analysis）是一种基于信息论的数据降维方法。KECA在特征空间进行核熵成分分析从而实现数据降维，具有良好的非线性处理能力，由于熵能够反映据所携带的信息量，因此KECA并不以保持特征空间中数据的方差最大化（如KPCA）作为特征选择的目标，而是以在降维后的特征空间中保持原数据的二次瑞利熵坐标轴作为投影方向，维数约减过程中选择前k个对瑞利熵贡献最大的特征向量，再将数据映射到这k个核主元方向上构成新的数据集。目前KECA已广泛应用于数据聚类、分类等模式识别应用中，并取得了良好的效果。核熵成分分析过程如下：
给定样本集D=（x1，x2，…，xN），p（x）为样本的概率密度函数，则样本的二阶瑞利熵为：
令V（p）=∫p2（x）dx，由于对数函数是单调函数，因此只需估计V（p）的值，进而估计H（p）。采用具有高斯分布帕尔森窗函数对p（x）进行估计，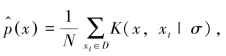
利用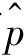
对V（p）进行估计得到：
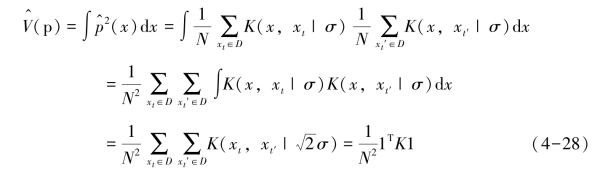
其中，1为全为1的N×1维向量，K为N×N的核矩阵，从而转为以核矩阵的形式描述2阶瑞利熵。将式（4-27）中的核矩阵K分解为K=EQET，其中E是特征向量[e1，…，eN]，Q是特征值
则有
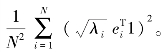
上述几个聚类算法和降维算法各有优缺点。由上节可知检测器集MS=∅将模式空间U划分为L个边长为
的n维超级立方体C，每一个C代表了一个检测器的覆盖域，也即是对模式空间U进行了网格化。在S≠∅的实际环境中，设某一正常模式s∈S为U中的一个点，如果该点被某一个C包含，即s∈C，我们说该C对应的检测器d识别模式s，即identify（d，s），也就是说检测器d的识别域与自我空间S相交，发生了自身反应，那么该检测器d就不是一个有效的检测器。免疫模型在产生新检测器时应避免对其在空间A中索引值的选择，这是一个否定选择的过程。
由于正常模式集即训练集Strn来自复杂且庞大的审计数据源，不可避免地包含一些噪声数据和异常数据，为了使该否定选择的过程不敏感于这些噪声数据和异常数据，必须设定某一噪声阈值来屏蔽这些干扰，当Strn中的样本点落在某一C中数目达到某一规定的噪声阈值时，则对应的检测器无效，即认为该C是一个自我子空间，否则该C对应的检测器是有效的。结合IAIDM模型中最小候选检测器集合M的特点，本书借鉴基于KECA的CLIQUE的聚类方法，提出了基于最小候选检测器集的否定选择算法MBNSA（M-Based Negative Selection Algorithm Based），并对MNSA的算法性能如精度、效率以及模糊性和动态更新等诸方面进行了详细的分析，下面的章节给出了具体描述。