4.5.1 算法描述
模式空间U⊆[0.0，1.0]n是一个n维的单位特征度量空间，其各维方向上的张量或坐标轴长度l=1，将模式空间U划分为一簇互不交叠的矩阵空间，即将各维坐标轴等距离划分为l个间隔，间隔宽度为h，设h=2ε/n，则各维方向上的间隔总个数
被划分为L=ln个矩阵空间C，每个C代表了一个候选检测器的覆盖域，则｜MS=∅｜=L。给各维上的间隔依此从0到l-1进行编号，用{r1，r2，…，rn}来确定各个C在U中的位置，其中ri=0，2，…，l-1，记为C：{r1，r2，…，rn}。
设训练集
是n维模式空间U中的一个点集，其中点
代表自我模式，其中
1，2，3，…，n）为点sj在第i维的坐标分量。如果一个矩阵空间C：
包含点sj，则有
其中1≤i≤n。所谓的网格密度是指矩阵空间C中包含的样本点sj的数目，记为m（c）。
设定一个密度阈值δlow来消除噪声数据和异常数据对否定选择结果的影响，则自我集合定义为
对应的检测器集是无效，因此M的范围为
M的空间覆盖整个N，即N=M，N是未知的。已知自我空间S=Cself，且MS=∅=U，由N=U-S，则M确定为：
从样本的空间分布来看，各样本点在各个聚类的中心区域呈密集分布，沿各维方向向边界移动时，样本的分布逐渐变得稀疏，也即集合Cself中各单元的空间位置是有规律的，在U中形成几个子空间，子空间的边界为m（c）等于δlow的c集合。MBNSA首先对集合Cself中各元素进行聚类处理以规律化Cself的空间位置信息。这里相关的定义。
定义4.13：设c1、c2为两个空间单元，c1与c2间的距离定义为：
dist（c1，c2）=Euclidean-distance[mean（c1），mean（c2）]，其中mean（c）为空间单元c的几何中心。
给定一个距离阈值τ，则c的邻域可定义为
在本模型中设
二维平面中，near（c）的示意图如下。
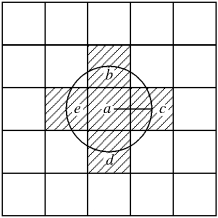
图4-5 空间单元的领域示意图
τ=2ε/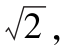
空间单元a的领域包括b、c、d、e几个单元
定义4.14：给定距离阈值τ和密度阈值δlow，c与c′之间有如下的一些关系：
（1）若c′∈near（c）且c′，c∈Cself，则称c′是从c出发关于τ直接密度可达（directly density reachable）。
（2）若存在一个空间链c1，c2，…，ck∈Cself，且c1=c，ck=c′。若ci＋1是从ci出发，是关于τ和δlow直接密度可达，则c′是从c出发，关于τ和δlow密度可达（density reachable）。
（3）若存在c′，c，c″∈Cself，若存在c′和c都是从c″出发，关于τ和δlow密度可达，则称c′和c是关于τ和δlow密度相连（density connected）。
（4）若c∈Cself，而near（c）=∅，则称c包含的样本点为孤立点，暂时不属于任何样本类。对于入侵检测系统来说，可能是由于训练集的不完备性造成的，或是较强的噪声区。
定义4.15：关于τ和δlow密度可达和相连的空间单元所形成的所有集合F1，F2，…，Fm⊂Cself，则F1∪F2∪…∪Fm称作一个关于τ和δlow基于密度的簇（density_based cluster）
下面给出自我空间集合Cself的聚类步骤：
步骤1：预处理过程。将训练集Strn中的每一个点映射到各个空间单元中，形成非空的集合
并存储Cne中各个空间单元的信息：m（c）及
可采用k-d树索引结构。
步骤2：聚类过程。给定距离阈值τ和密度阈值δτ，基于密度可达和密度连接对Cne中的各个单元进行聚类。在初始情况下，所有的单元皆处于未分类状态，设置聚类条件V：m（c）≥δlow且处于未分类。
（1）搜索k-d树，选择一个满足条件V的单元c且near（c）≠∅作为某类的聚类起始点。将集合
且满足条件V}归于c所属的类，并从集合R中随机选择某一c′作为下一步的搜索出发点，将集合R′=
且满足条件V}归于c′所属的类，再选一c″为出发点，直至near（ci）中没有满足条件V的空间单元为止，则形成同一类的空间集合c1，c2，…，ck。
（2）如果Cne中存在满足条件V的单元c，则转到（1）。
（3）结束。自我空间集合Cself经上述处理，聚为m个类F1，F2，…，Fm，有F1∪F2∪…∪Fm=Cself。
在4.3节中，利用整数索引空间A，由公式（4-9）从MS=∅中十分简便地产生了新的检测器，而不必让系统记忆MS=∅中的每一个元素，MBNSA算法同样利用了整数索引空间A来产生新的检测器。将各聚类集合F1，F2，…，Fm中各单元的位置信息{r1，r2，…，rn}映射到整数索引空间A：[0，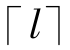
-1]n中，形成m个点集Aj（j=1，…，m），Aj中各点在空间A中连续。由这些点产生的检测器会发生自身反应，需要避免对这些点的选择。通过对点集Aj的分布性质进行分析，可以进一步规律化A中自反应点的空间位置信息，提高MBNSA的算法效率。
定义4.16：Aj分布的投影区。某一个点集Aj中的所有点在i维上投影区域的下限和上限分别为Lowi和Highi，则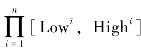
是A空间中一个包含该点集所有点的、连续且最小的区域，即有以下条件成立：
（1）对于任意的点a=（a1，a2，…，an）∈Aj，有a∈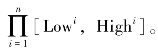
（2）对于任意的点
有x∉Aj。
（3）不存在任何超立方体区域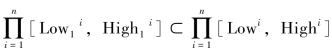
能够包含该点集的所有点。
定义
为该点集Aj的投影区，Lowi和Highi分别为投影区在向量维上的下界和上界。
当模型随机在空间A中选择的一点a=（a1，a2，…，an），检查该点是不是自反应点，通过定义4.16可以较大地缩小搜索范围，提高MBNSA的算法效率。这里应注意到由于Aj的空间分布不规则，它们的投影区可能发生部分重叠的现象。MBNSA算法的整个过程为：
MBNSA算法的实现可分为两个阶段：训练期和检测期，在训练期主要是完成自我空间的界定，其时间复杂度为O（NS＋｜Cself｜log｜Cne｜），其中NS表示训练集Strn中样本数目，通常地｜Cself｜和｜Cne｜≪Ns，空间复杂度O（｜Cne｜）。在检测期主要是完成有效检测器的产生，其时间复杂度的计算与Aj的空间分布有关，如果Aj的空间分布极不规则，即所有的投影区间存在公共的重叠区域，则最大时间复杂度为O（｜Cself｜）；如果Aj的空间分布规则，即所有的投影区间不发生重叠的现象，则最小时间复杂度为O[m＋max（｜A1｜，｜A2｜，…，｜Am｜）]，m为自我子空间的个数。
MBNSA算法结合免疫模型检测器d的空间覆盖域C定义，来网格化模式空间U，用空间网格内的样本统计信息来代替该网格内的所有点，样本聚类的效率高，并且可以处理高维的数据。MBNSA只是寻找大于一定密度阈值的集合Cself，其数量远小于Strn中的样本总数。因此MBNSA与传统免疫模型中复杂繁重的否定选择过程相比，有效检测器的产生效率得到很大的提高。