蒸散发遥感模拟结果精度验证

遥感蒸散发模型的精度不仅取决于蒸散发模型本身，也取决于遥感对地表信息反演的广度和深度。长久以来对蒸散发量的验证分析，都是蒸散发研究工作中的重点与难点，不仅需要高端的设备仪器，也需要大量的野外调查工作。

Penman-Monteith模型虽属于经验公式，却具有坚实的物理基础，作为统一的、标准的计算方法，无须进行地区校正和使用当地的风函数，也无须改变任何参数即可用于世界各地，估值精度较高且具有良好的可比性。同时，Penman-Monteith模型全面考虑影响蒸散发量的大气物理特性和植被的生理特性，具有很好的物理依据，能比较清楚地了解蒸散发量的变化过程及影响机制，为非饱和下垫面蒸散发的研究提供了良好对比参照。因此，在现有条件的基础上，对Penman-Monteith模型所计算出的蒸散发数据作为参照，对精河地表蒸散发模型进行验证，主要采用“面”的验证和“点”的验证相结合的方法。

“面”的验证对Penman-Monteith模型、SEBAL模型、SEBS模型反演的研究区整体蒸散发数据进行验证，并且横向与蒸发皿数据进行对比，探讨分析蒸散发量模拟结果是否处于准确范围，并对模拟精度做出评价。Penman-Monteith模型、SEBAL模型、SEBS模型蒸散发数据都小于蒸发皿数据0.32～2.461 mm，说明反演数据是符合实际的。SEBAL和SEBS两个模型的蒸散发数据较为接近，相差不足10％，平均比Penman-Monteith模型蒸散发数据低0.679 mm，且多年趋势与Penman-Monteith模型较为一致。但从总体精度来看SEBS模型蒸散发数据的精度高于SEBAL模型9.01个百分点（图7-20）。

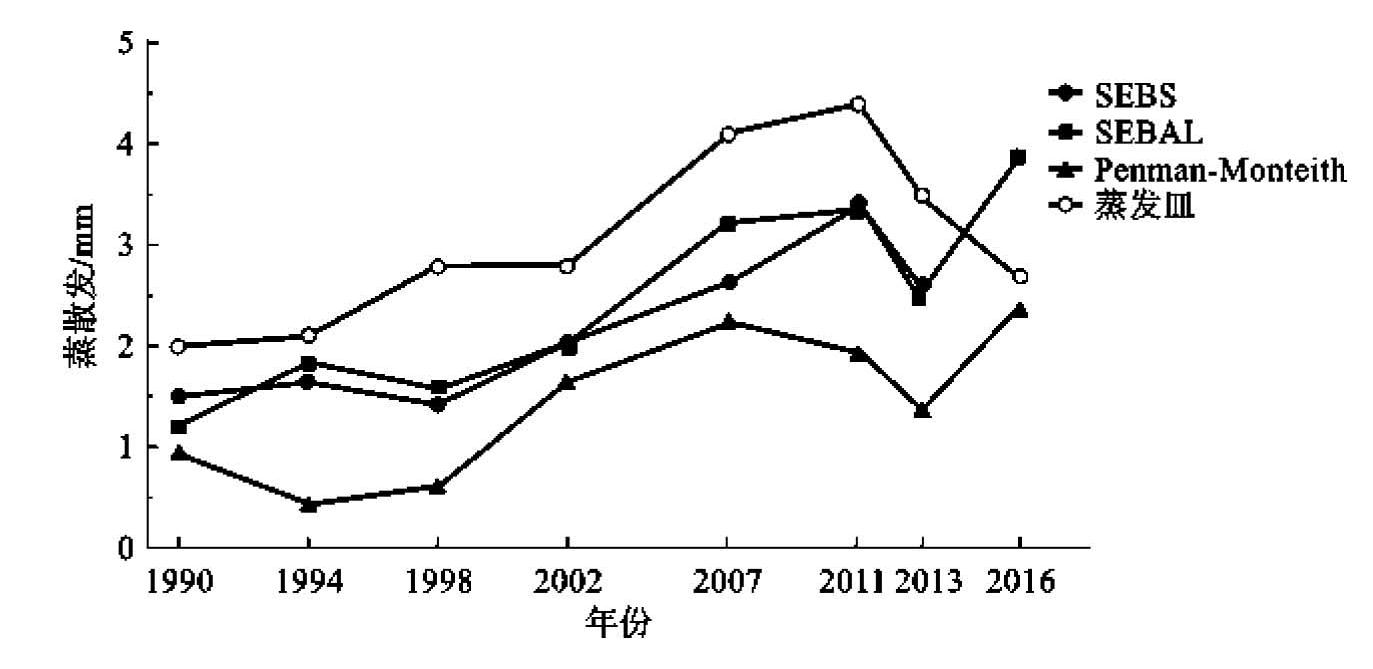
图7-20　精河县蒸散发数据精度验证

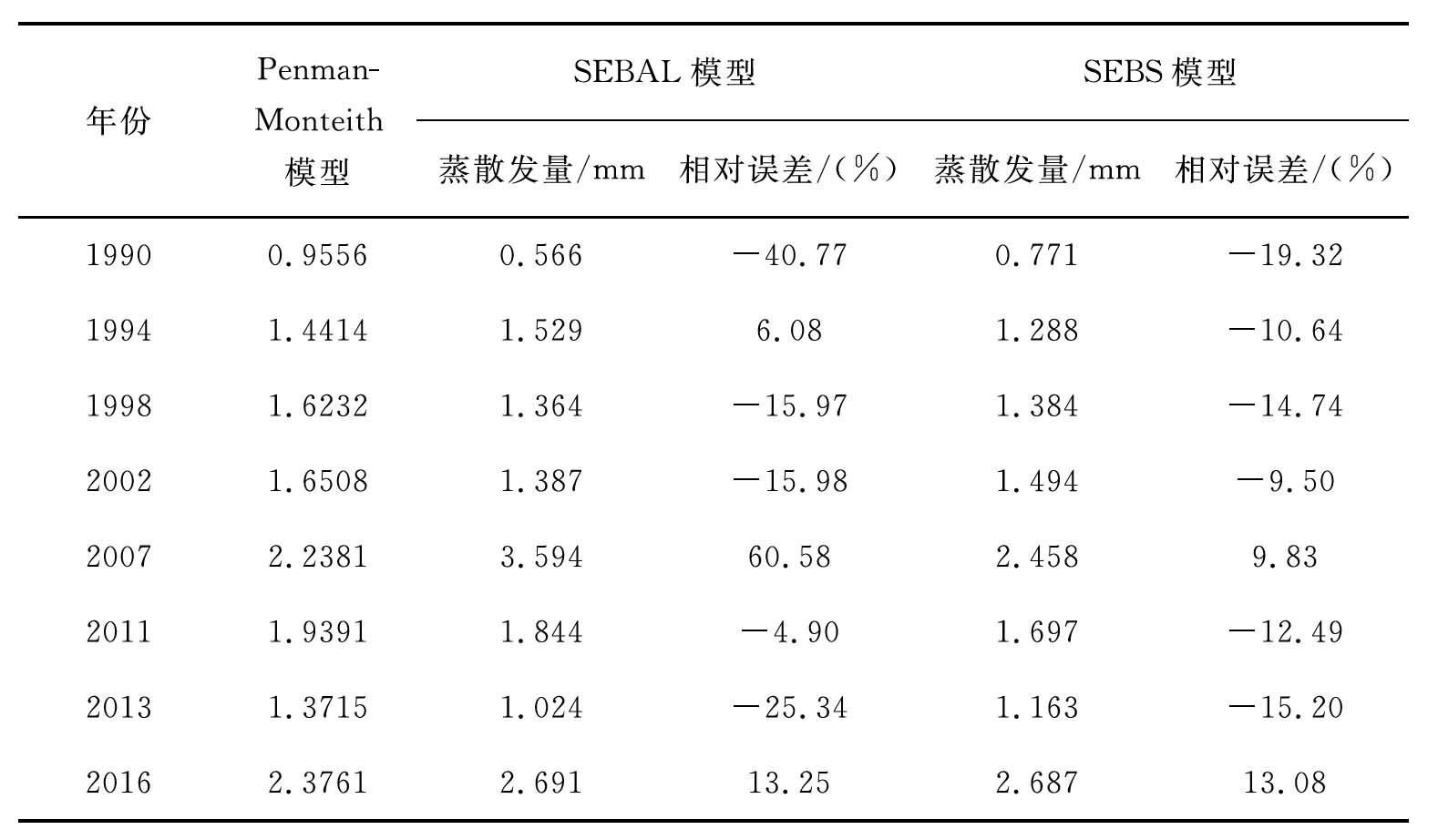
“点”的验证主要通过将气象站点精河站（站点编号：51334）的实测蒸散发数据与在该坐标下的Penman-Monteith模型、SEBAL模型、SEBS模型结果对比进行验证分析（表7-6）。其中，SEBAL模型蒸散发量相对误差最高为60.58％，最低为-4.90％，平均误差率为22.85％，大于20％，而SEBS模型蒸散发量相对误差最高为-19.32％，最低为-9.50％，平均误差率为13.09％，均在20％之内。

表7-6　Penman-Monteith、SEBAL、SEBS模型蒸散发数据精度验证

无论是“面”的验证还是“点”的验证，SEBS模型与其他研究者的验证精度都相近，相对于SEBAL模型而言，该模型有很好的适应性，能够达到本研究区尺度上蒸散发量的扩展要求，对于精河地区是适用的。