2.5.1 应召搜潜时潜艇位置散布建模
反潜巡逻机应召搜潜,是指反潜巡逻机根据其他兵力(包括其他反潜飞机)、兵器得到的潜艇部分信息(通常是发现潜艇(或可疑潜艇)的时刻及其位置(初始位置)、位置误差(初始位置误差)等),前往潜艇(或可疑潜艇)存在区进行的搜索,首要目的是发现潜艇(或可疑潜艇)。
执行应召搜潜任务时,在搜索海域内某一时刻,在概略的位置上存在过潜艇的活动,但由于潜艇活动的随机性,潜艇的当前位置呈一定分布,这使得反潜兵力到达搜索区域后需要再次搜索定位。反潜巡逻机执行应召搜潜任务抵达搜索海域时,潜艇散布区域的大小主要由潜艇初始位置误差、航速、航向、应召延误的时间长短决定。潜艇的速度越快,延误时间越长,潜艇的散布范围就越大;反之,则越小。因此,应根据执行任务时所获得的潜艇初始位置等信息和上述影响因素来确定潜艇位置散布。
2.5.1.1 应召搜潜时潜艇的初始位置散布模型
通常以潜艇初始位置为基准点,并设为坐标原点,设定潜艇的初始位置服从二维N(0,σ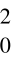
)正态分布[51],则数学期望值E(x)=0,初始位置(x0,y0)的联合概率密度函数为
式中,x0、y0相互独立且同分布,当σ0x=σ0y=σ0时,均服从N(0,σ2 0)分布。σ0通常由其他兵力测量和计算潜艇的位置误差产生。当σ0=2 000m时,潜艇目标初始位置散布如图2-5所示。
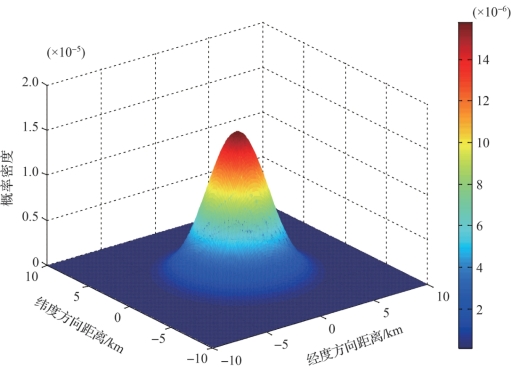
图2-5 应召搜潜时潜艇目标初始位置散布规律仿真图(附彩图)
把直角坐标系变换到极坐标系(R,Θ),可得(R,Θ)上的联合密度函数:
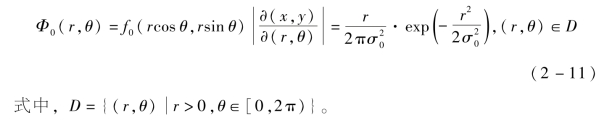
假设I是单位函数,则R、Θ的概率密度函数计算为
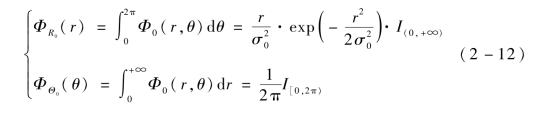
综上,ΦR0(r)ΦΘ0(θ)=Φ0(r,θ),R和Θ相互独立,R服从瑞利分布,Θ服从[0,2π)区间上的均匀分布。
2.5.1.2 应召搜潜时潜艇运动后的位置散布模型
反潜巡逻机获得潜艇的初始信息后,待到达作战海域使用搜潜设备进行搜索作战时,已经延误t0时间,目标潜艇的位置已发生变化。潜艇的位置将以初始位置散布为中心,以机动速度继续扩大。位置散布区域扩大的大小与潜艇的速度和延误时间(从获得潜艇初始位置到反潜巡逻飞机开始探测的时间)有关[51]。因此,潜艇的位置散布包含初始散布和运动不确定性引起的散布两部分。在此对潜艇速度未知(或已知)和以任意航向(或已知概略航向)的三种最常见的潜艇位置散布情况建模。
1.潜艇速度未知,航向在[0,2π)区间服从均匀分布时
反潜巡逻机经过t0时间开始搜索后,潜艇位置的概率密度函数为[51]
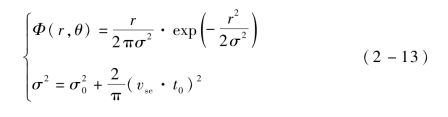
式中,vse——潜艇的经济航速,即潜艇速度的数学期望值;
t0——反潜巡逻机从获知潜艇初始信息到飞往作战海域开始搜索的时间。
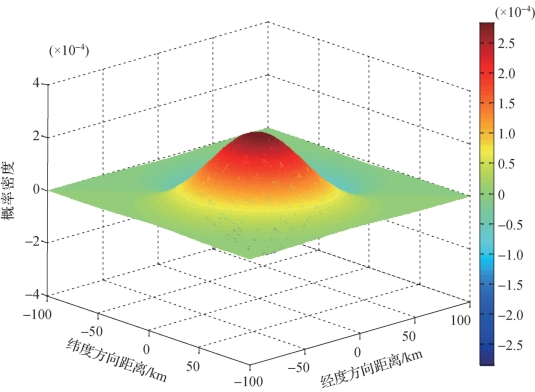
图2-6所示为速度未知条件下,潜艇位置概率密度分布的仿真情况,由图可知,存在潜艇的概率最大的位置在峰顶。
图2-6 速度未知条件下,潜艇位置概率密度分布示意图(附彩图)
潜艇经济航速(即潜艇速度的数学期望值)的相关计算如下:设潜艇的速度为v,则r=v·t0,σ0=σv·t0,代入式(2-11)可得
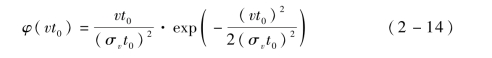
式中,t0为常量,因此可得潜艇速度的概率密度函数为
若潜艇保持恒向恒速航行,取潜艇的水下经济航速vse作为潜艇分布函数的数学期望,即
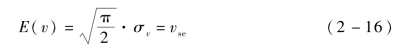
求得
2.潜艇速度已知,航向在[0,2π)区间服从均匀分布时
假设潜艇匀速直线运动,速度是v,初始位置散布服从N(0,σ
),则潜艇位置散布的概率密度为
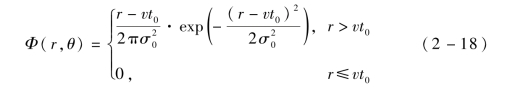
假设反潜巡逻机应召延迟时间为t0=0.8 h,取v=11 km/h,则已知潜艇速度条件下,潜艇位置概率密度分布的仿真情况如图2-7所示,由图可知,存在潜艇的概率最大的位置在环形峰顶。
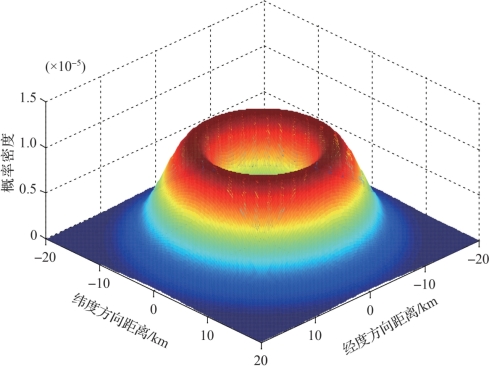
图2-7 速度已知条件下,潜艇位置概率密度分布示意图(附彩图)
3.已知潜艇速度和概略航向时
假设潜艇作匀速直线运动,速度是v,潜艇初始位置散布服从N(0,σ
),当已知概略航向α时,考虑航向误差服从正态分布,根据“3σ”原则,其标准偏差σα=Δα/3,而速度与航向误差两者是独立的,故潜艇位置散布的概率密度为
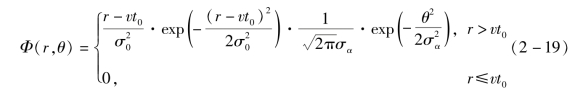
假设反潜巡逻机应召延迟时间为t0=0.8 h,取v=11 km/h,σα=0.1π,则已知潜艇速度和概略航向条件下,潜艇位置概率密度分布的仿真情况如图2-8所示。
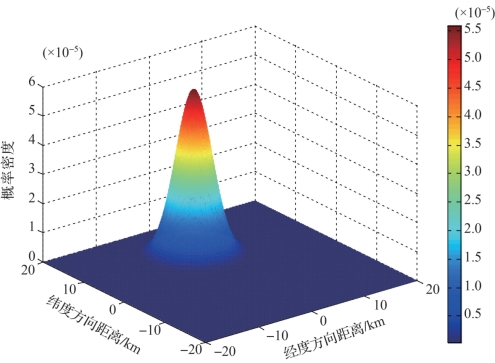
图2-8 已知潜艇速度和概略航向条件下,潜艇位置概率密度分布示意图(附彩图)