6.2.1　贝叶斯粗糙集

粗糙集(rough set,RS)理论是波兰数学家Paw lak于1982年提出的一种数据分析理论[122],现已成为一种新的处理模糊不精确、不确定或不完全数据的数学工具。粗糙集理论的中心问题是分类分析,而粗糙集模型在实际应用中存在一定的局限性,它所处理的分类必须是完全正确的或肯定的,即“包含”或“不包含”,而没有某种程度上的“包含”或“属于”[123]。这限制了它在实际中的应用,因为大部分指标之间并不一定存在严格的函数依赖关系,而是表现出近似依赖关系。于是,Ziarko对粗糙集模型进行推广,于1993年提出变精度粗糙集模型(variable precision rough set,VPRS)[124],该模型在粗糙集模型的基础上引入阈值β,并将其定义为错误分类率且β∈[0,0.5),即允许一定程度上错误分类的存在,所以变精度粗糙集具有很强的抗干扰能力。然而,在一般情况下,我们只需要根据所获得的信息去处理问题,而不受预先给定某个参数的限制,所以在大多数的实际应用中,变精度粗糙集也有其局限性,这限制了它的应用范围。于是学者们从不同的角度对其进行推广,其中,文献[125]把变精度粗糙集中的参数β用先验概率代替,提出了贝叶斯粗糙集(Bayesian rough set,BRS)模型。

定义6.1　假设(U,A∪D)是信息系统,U是对象的非空有限集合,U={x1,x2,…,xn},A是条件属性的非空集合,A={a1,a2,…,ap},D是决策属性集合,D={d1,d2,…,dp},对于B⊆A,记:

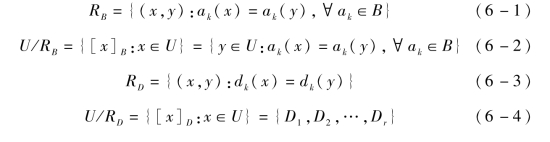
式中,ak(x),dk(x)——属性ak和dk在U中x处的取值,k=1,2,…,p。

对于∀X⊆U,β∈(0.5,1],记:

对于0＜P(x)＜1,记: