5.3.5 仿真验证与分析
基于所建决策模型的实用性以及对海洋环境的适应性,选取存在跃变层的Ⅲ型声速梯度,海区深度为400m,海底平坦,底质淤泥。夏季,海况2级,不考虑受到海流影响引起的浮标位置变动,以两架反潜巡逻机自主模式协同搜索静音潜艇为例。仿真过程如下:
第1步,进行指标归一化处理。因为搜索能力、隐蔽性、可操作性、经济性指标的物理量纲不同,所以必须先进行归一化处理。一般情况下,指标可以分为效益型、成本型、固定型和区间型。效益型指标的值越大越好;成本型指标的值越小越好;固定型指标的值不能太大,也不能太小,其值越接近某个固定值越好,该固定值为其最佳值;区间型指标是其值越接近某个固定区间越好,该固定区间是其最佳区间值。搜索能力、隐蔽性、可操作性、经济性4个指标都是越大越好,是效益性指标。设方案集为C={c1,c2,…,cn},指标集为H={h1,h2,…,hm},决策矩阵为H=(hij)m×n,hij是方案cj的第i个指标值。在此把决策矩阵转变为相对隶属矩阵(即T=(Tij)m×n)归一处理,处理如下:
![]()
式中,pi——由决策者确定的参数;
![]()
第2步,通过专家和决策者打分,确定常权情形下属性Shapley值的判断矩阵R。
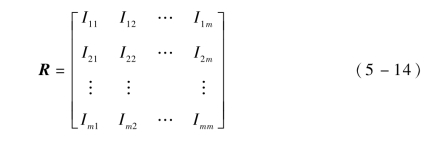
式中,Iij——指标hi与hj的Shapley值之比,显然Iii=1。
然后,采用层次分析法[121]判定矩阵R的一致性。当矩阵R满足一致性时,就依据矩阵R计算常权情形下各指标的Shapley值。
第3步,指标的模糊测度计算。根据式(5-11),用MATLAB编程求解各指标(集)的模糊测度。
第4步,用Choquet模糊积分计算各个方案的优势值,依据方案的优势值对方案进行排序和选优。
(1)假设目标潜艇处于深度工作状态,两架反潜巡逻机携带数量充足的声呐浮标(满足任务需求),潜艇目标散布范围很广,隐蔽性较好,进行验证性分析。基于5.3.1节介绍的6个协同搜索方案,所得决策方案仿真结果如表5-2所示。
表5-2 6个决策方案的仿真结果

由表5-2可知,6个方案中的最优方案是方案1,即最优方案是雷达、红外搜索仪、电子支援系统和声呐浮标组合的搜索方案,在对水下目标搜索的同时,对水面情况进行监控,及时捕捉可能上浮的潜艇。实际上这也是大中型反潜飞机最典型的搜索方式。(https://www.daowen.com)
(2)假设目标潜艇处于深度工作状态,声呐浮标的存有数量不充足,潜艇目标散布范围很小,隐蔽性中等,进行验证性分析。基于5.3.1节介绍的6个协同搜索方案,所得决策方案仿真结果如表5-3所示。
表5-3 6个决策方案的仿真结果

由表5-3可知,6个方案中的最优方案是方案6,在声呐浮标数量不充足的情况下,推荐只使用磁探仪进行目标潜艇的搜索。
(3)假设目标潜艇处于水面航行状态,声呐浮标携带数量充足(满足任务需求),潜艇目标散布范围很小,隐蔽性好,进行验证性分析。基于5.3.1节介绍的6个协同搜索方案,所得决策方案仿真结果如表5-4所示。
表5-4 6个决策方案的仿真结果

由表5-4可知,6个方案中的最优方案是方案2,虽然声呐浮标数量充足,但对于水面目标还是推荐雷达、红外搜索仪和电子支援系统组合协同进行搜潜。
(4)假设目标潜艇处于水面航行状态,声呐浮标存有数量不充足,潜艇目标散布范围很小,隐蔽性好,进行验证性分析。基于5.3.1节介绍的6个协同搜索方案,所得决策方案仿真结果如表5-5所示。
表5-5 6个决策方案的仿真结果

由表5-5可知,6个方案中的最优方案是方案2。综合表5-4、表5-5可知,对处于水面状态的目标潜艇,都应该采用水面搜潜设备进行协同搜索,且与声呐浮标的数量无关,该结果与实际情况相符合。
本方法不需要确定各指标的权重,评估结果不依赖各指标的权重,可以在各指标权重完全未知的情况下对方案进行选择,从而解决了多指标方案优选过程中指标权重难以确定的问题,而且能较好地描述各决策指标之间的相互关联现象,使决策更加客观和准确,可为合理、科学地选择决策方案提供参考。
综上,基于模糊测度与模糊积分的反潜巡逻机协同搜潜智能决策方法可有效解决在信息不确定的情况下,快速有效地对多个方案进行最优决策的问题,可以选出最优方案,而且该方法简单、易行。
