4.3.2 云贝叶斯网络
4.3.2.1 模糊贝叶斯网络方法
模糊贝叶斯网络方法可以对模糊域和概率域数据进行融合处理,符合人的思维推理,便于理解,具有数据表示力强、数据连续和时间累计等特性,因此具有一定的实用性。
结合模糊逻辑和贝叶斯网络在知识表示和推理上的优点,我们可以引入模糊概率转换公式,运用该公式,也可以将模糊逻辑和贝叶斯网络集成为模糊贝叶斯网络。
设U={u1,u2,…,un}是一个离散有限集合,A是U的一个模糊集合,又称模糊子集,可以由其隶属度函数定义,X是取自U中的一个变量,p(ui)表示X=ui时的概率,π(ui)表示X=ui时的可能性,μ(ui)是模糊集合A上的隶属度函数,是ui对A的隶属度。
Zadeh[93]认为可能性理论是模糊集理论的扩展,因此可能性理论中可能性分配π可以由模糊集上的隶属函数决定。于是得到
![]()
Geer等[94]认为信息中的不确定性在一两种理论的相互转换过程中应保持不变,并在可能性概率转换过程中提出“信息转换保护”(information preserving transformation)。其转换公式为
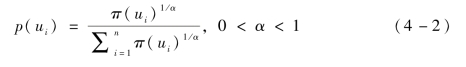
式中,α——可能性概率转换一致性条件满足的程度,0<α<1。α趋向0,则转换的概率p(ui)间差异较大;α趋向1,则p(ui)间差异较小。
将式(4-1)与式(4-2)合并,得到
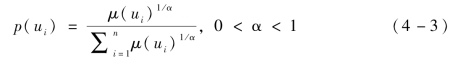
根据式(4-3),可以把模糊逻辑和贝叶斯网络集成为模糊贝叶斯网络,用以解决态势评估问题。
4.3.2.2 云贝叶斯网络方法
云贝叶斯网络[95-97]是由模糊贝叶斯网络启发而来的,是对模糊贝叶斯网络的一种改进。把模糊集理论和贝叶斯网络[98-99]相结合,建立模糊贝叶斯网络,对实际问题进行分析推理,这已成功应用在态势评估中[100-101]。但是以模糊集理论为基础的贝叶斯网络在不确定知识表达上,只能对知识在模糊性方面进行解释,不能在随机性方面进一步解释。云模型是在定性概念和定性概念的定量表示之间形成某种映射,是一种双向认知模型,揭示了模糊性和随机性之间的关系,而且能够用模糊数学和概率论给出合理的解释,在知识的表示上有很大优势,并在很多学科领域得到应用[102]。贝叶斯网络与人类思维模式相近,实质上是一种不定性的因果关联模型,它本身是将多元知识可视化为一种知识表达和推理模型,但其模型的结构主要包含各节点之间的因果关系及条件相关关系,是众多不确定推理方法中应用最为广泛的一种理论方法[103]。这两者各有优势,云理论在知识表示上优于贝叶斯网络,而贝叶斯网络在推理能力上优于云推理,因此云贝叶斯网络模型克服了单一的云模型在推理能力上的不足以及贝叶斯网络在知识表示上的缺陷,综合了云理论所具有的模糊性和随机性的知识表达能力以及贝叶斯网络所具有的推理能力,成为一种新的能够同时考虑模糊性、随机性的不确定性推理模型。
云贝叶斯网络的基本思想:首先,对网络中的连续型变量进行归一化处理;然后,运用云模型转换对归一化变量进行离散化处理,使网络统一为离散型贝叶斯网络,同时通过确定度-概率转换公式把确定度转换为概率。其本质是把云模型融入贝叶斯网络节点参数,把云模型转换为单个贝叶斯网络节点的条件概率表(CPT),从而利用云的知识表达能力实现了用尽量少的专家参数表达复杂条件概率表的目的,大大降低了专家设计条件概率表的工作量,提高了贝叶斯网络的设计效率。云模型的条件独立关系,即贝叶斯网络结构(有向无环图),可由专家根据因果关系设计,其条件概率表可根据图4-9所示的过程生成。该过程分为权值计算、云模型转换、条件概率转换三部分。

图4-9 条件概率表生成过程
1.状态组合权值
权值共分为4部分:父节点权值(WA)、状态权值(WS)、状态影响因子(WAS)、状态组合权值(WCS)[104]。权值计算的最终结果是状态组合权值,它是构建云族及生成条件概率表的基础。(https://www.daowen.com)
WA表示单一父节点对子节点的影响程度;WS表示父节点的状态变化对子节点的影响程度,每种状态划分对应一组状态权值。这两种权值均由专家知识构建,WA和WS是整个云贝叶斯网络参数生成模型的输入。
WAS是父节点权值与其各状态权值的乘积,它表示单个父节点各状态分别对子节点的影响程度。设第i个父节点的权值为WAi,且该父节点有S种状态,WSj表示第j种状态的状态权值,则该父节点各状态的影响因子为:{WAi×WS1,WAi×WS2,…,WAi×WSS}。
WCS表示所有父节点的状态组合对子节点的影响程度,其值为该状态组合下各节点状态的WAS之和。设节点B有n个父节点,其第q个状态组合中各父节点状态的状态影响因子分别为{was1,was2,…,wasn},则该状态组合的状态组合权值为

2.云贝叶斯网络模型转换
云贝叶斯网络模型转换包括两部分——云模型转换、条件概率转换[104]。云模型转换是指在状态组合权值的论域中定义一个云族,并根据云族的定义设计一组云发生器,每个云发生器与所求节点的状态划分一一对应。条件概率转换是把父节点的状态组合权值代入云发生器,得到一个云滴,即该状态组合权值下所求节点的确定度;然后,将各状态的确定度归一化,得到条件概率表的一个表项;重复上述步骤,计算得到所有表项,即可求出整个条件概率表。生成CPT的具体步骤流程如图4-10所示,详细描述如下。
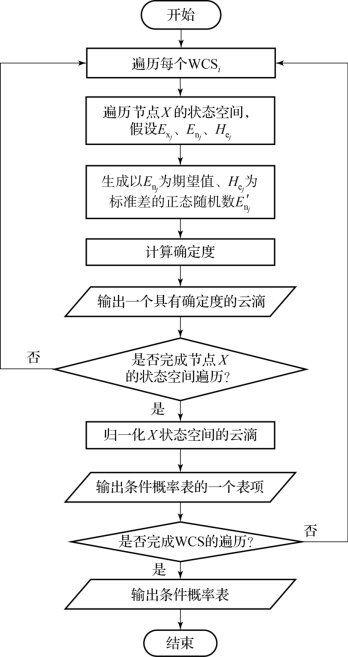
图4-10 生成CPT过程示意图
第1步,遍历WCS的每个WCSi。
第2步,遍历节点X的状态空间,假设第j个状态云发生器的数字特征为Exj、Enj和Hej。
第3步,生成以Enj为期望值、Hej为标准差的正态随机数E′nj。
第4步,计算WCSi的确定度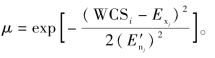
第5步,输出一个具有确定度的云滴drop(WCSi,μ)。
第6步,如果完成节点X的状态空间的遍历,则执行第7步,否则继续遍历。
第7步,归一化X状态空间的云滴。
第8步,将归一化的结果输出到条件概率表,作为其中一个表项。
第9步,如果完成WCS的遍历,则执行第10步,否则继续遍历。
第10步,输出条件概率表。
云贝叶斯网络构建完成后,根据收集到的证据进行评估推理运算。云贝叶斯网络推理算法与贝叶斯网络推理算法的区别只有条件概率表的构建过程不同,因此云贝叶斯网络算法可以使用贝叶斯网络推理算法进行概率推理,求得查询变量的后验概率,完成最终的任务。
