附录C　模糊测度与模糊积分

附录C　模糊测度与模糊积分

1.模糊测度

测度是数学的基本概念之一,通常分为经典测度与模糊测度。经典测度主要研究一般集合上的测度,是勒贝格测度的进一步抽象和发展。简言之,测度是可测的几何区域上的某种测量尺度,概率论中的概率测度是经典测度的一个特例,并且满足可加性。经典测度之所以受关注,主要是因为其具有可加性,但在具体实践中,这种可加性的约束可能太强,所以难以把握。虽然可加性能够很好地描述没有误差的理想情况下的测量问题,但是实际情况下测量误差经常是不可避免的,所以经典测度并不能充分描述一些实际物理条件下的测量问题。另外,一些主观评判、非重复性试验的测量,本质上是非可加的。相较于经典测度,模糊测度的表现特征无法直接进行加减性运算,所以也被称为非可加性测度,属于模糊数学的范畴。模糊测度包括似然测度、信任测度、可能性测度、2-可加测度、λ-模糊测度等。从集合的角度看,模糊测度可视为经典概率测度中集合点对集合集在隶属关系研究上的一种延伸,通过模糊测度可以描述某一集合点对于该集合集的隶属程度,或者说以模糊测度对该集合集进行某种度量。而当这种描述或度量可通过一组集合数来表示时,传统的集合逻辑与方法便进一步推广为以研究隶属函数与隶属度为基础的模糊集概念。由此,模糊测度在应用解决实际问题中的优势便显现出来。其定义如下:

定义C.1[109]　设X是一个非空集合,Y为X的所有子集组成的σ-代数,Y上的一个非负广义实值集函数μ:Y→[0,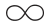)称为一个模糊测度,如果它满足以下条件:

①(平凡性)μ(∅)=0;

②(单调性)∀A∈Y,B∈Y,A⊂B⇒μ(A)≤μ(B);

③(下连续性)∀An∈Y,A1⊂A2⊂…⊂An⊂…,n=1,2,…

④(上连续性)An∈Y,A1⊃A2⊃…⊃An⊃…,n=1,2,…,且∃n0,使得: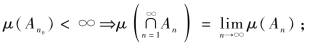

则称(X,Y,μ)是模糊测度空间,(X,Y)称为可测空间。如果μ只满足条件①～③,则称μ是可测空间(X,Y)的下半连续模糊测度;如果μ只满足条件①、②、④,则称μ是上半连续模糊测度;如果μ(X)=1,则称μ为正则模糊测度;如果μ(X)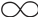＜,则称μ是有限测度。当X是一个有限集合时,Y是X的幂集P(X),条件③、④自动满足。

由上述可见,模糊测度就是舍弃了经典测度的可加性,由更广泛的单调性取代,从而更符合解决实际中的问题。

1974年,Sugeno提出了λ-Fuzzy测度,即gλ模糊测度,其定义如下:

定义C.2[109]　设X是一个非空集合,Y为X的所有子集组成的σ-代数。(X,Y)为一可测空间,λ∈(-1,+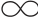),集函数gλ:Y→[0,1]称为(X,Y)上的gλ测度,如果它满足以下条件:

①gλ(X)=1;

②A,B∈F,A∩B=∅⇒gλ(A∪B)=gλ(A)+gλ(B)+λgλ(A)gλ(B);

③{An,n≥1}⊂Y,An↑A(An↓A)则gλ即gλ模糊测度。把模糊测度扩展到gλ模糊测度是又一个新开辟的研究课题。

定义C.3[109]　若对∀E1∈Y,E2∈Y,E1∩E2=∅,有μ(E1∪E2)=μ(E1)+μ(E2)成立,则称μ是可加的。

若对∀E1∈Y,E2∈Y,E1∩E2=∅,有μ(E1∪E2)≤μ(E1)+μ(E2)成立,则称μ是次可加的。

若对∀E1∈Y,E2∈Y,E1∩E2=∅,有μ(E1∪E2)≥μ(E1)+μ(E2)成立,则称μ是超可加的。

若对∀E∈Y,F∈Y,E∪F∈Y,E∩F=∅且μ(F)=0,有μ(E∪F)=μ(E)成立,则称μ是零可加的。

显然,模糊测度是正规单调集函数,且空集的函数值为零。从决策角度来看,对任意准则子集E1∈Y,模糊测度值μ(E1)可以解释为集合E1的权重或重要性,单调性意味着子集的权重不能因为新准则的加入而减少。

定义C.4[109]　μ满足σ-λ律是指:存在使得对任意的E∈Y,F∈Y,E∪F∈Y,E∩F=∅,有μ(E∪F)=μ(E)+μ(F)+λμ(E)μ(F)成立,使得Y中任意不相交序列{E1,E2,…,En}的并集也在Y中,有

当且仅当μ满足σ-λ律,并且至少存在一个E∈Y使得时,称μ是Y上的gλ模糊测度。当gλ(X)=1且任意E∈Y有gλ(E)∈[0,1]时,称其为正则的gλ模糊测度。gλ模糊测度在单点集上的值gλ({xi})也称为模糊密度,记作gi,有下列性质:

定理C.1[109]　设X={x1,x2,…,xn},μ是Y上的gλ模糊测度,μ至少在两个单点集上的值大于零,即

①当＜1时,λ＞0,gλ模糊测度是超可加的;

②当=1时,λ=0,gλ模糊测度是可加的,退化为经典测度;

③当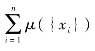＞1时,-1＜λ＜0,gλ模糊测度是次可加的。

由上可知,正则gλ模糊测度中未知参数λ的值完全由式(C-1)确定。

若X={x1,x2,…,xn}为有限集合,对于P(X)={E⊂X}上的gλ模糊测度,λ≠0,则任意E∈P(X),即映射:xi→gi=g({xi}),i=1,2,…,n,称为模糊密度函数。gλ模糊测度可完全由其模糊密度函数确定,即

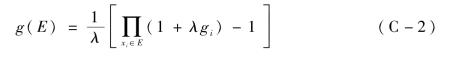
2.模糊积分

德国数学家Riemann研究傅里叶级数时,曾经尝试可以用傅里叶级数表示更广泛一类的函数。1853年,他撰写了论文《用三角级数来表示函数》,在文中给出了定积分的定义以及可积性准则,其中体现的积分思想使得他成为对近代积分学影响最大的数学家之一。但是,Riemann积分中存在一些缺陷,如积分与极限可交换顺序的条件太严、积分运算不完全是微分运算的逆运算等。于是,人们对其进行了改进。1902年,法国数学家Lebesgue成功引入一种新的积分,即Lebesgue积分[120]。

模糊积分的理论研究由来已久。美国计算机与控制论专家Zadeh提出了模糊集的概念,1965年,他在杂志Information and Control上的著名论著[110]标志模糊理论的诞生。1974年,Sugeno[111]提出了模糊测度的概念,在此基础上,Sugeno还定义了一种泛函,即Sugeno模糊积分。定义如下:

定义C.5　假设(X,Y)为一可测空间,μ:Y→[0,1]是模糊测度,f:X→[0,1]是可测函数,A∈Y,则f在A上关于μ的Sugeno模糊积分为

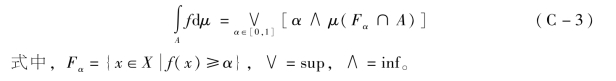
模糊积分主要在于把Lebesgue积分中的运算“+”“·”取代为“∨”“∧”,因而积分性质也就失去了可加性。Sugeno最早把模糊积分应用于主观评判过程,取得了较好的效果,因而这一理论也就备受人们重视。赵汝怀[129]把“∧”代之以普通乘法“·”,于1981年给出(N)模糊积分;张文修[130]给出T模糊积分,即用三角模“T”代替“∧”,Suarez与Alvarez[115-116]用“三角半模”代替“∧”,于1986年得到半模模糊积分。吴从炘[117]研究了模糊积分运算的特点,于1990年提出了一种称之为“广义三角模”的运算,即一个二元函数如果满足下述条件:

①当S[x,0]=0,x∈[0,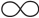),并且∃e∈(0,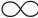)使得S[x,e]=x,x∈(0,);

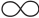②S[x,y]=S[y,x];

③x1≤x2,y1≤y2蕴含S[x1,y1]≤S[x2,y2];

④xn↑x,yn↓y蕴含S[xn,yn]→S[x,y];则称此二元函数为广义三角模。用广义三角模“S”代替Sugeno模糊积分中的运算“∧”,就得到广义模糊积分,因而它是Sugeno模糊积分的推广。基于gλ模糊测度的理论,俞新贞等[131]定义了gλ模糊积分。但Sugeno模糊积分不是Lebesgue积分的推广,当测度满足可加性时,Sugeno模糊积分并不能还原为Lebesgue积分,即使是广义模糊积分也不是一类特殊的Lebesgue积分[132],这样就限制了其在实际中的应用,为弥补缺陷,人们又进一步进行了研究,近年来,模糊积分得到迅猛发展。

3.模糊测度与Choquet模糊积分

法国数学家Choquet针对其提出的容度,又定义了一种积分,现被广泛称作Choquet模糊积分[118]。当模糊测度有经典的可加性时,Choquet积分就退化为Lebesuge积分,所以Choquet积分是Lebesuge积分的推广。随着Murofushi与Sugeno等人后续在模糊测度上的研究和对Choquet模糊积分的改进,其得以在传统Lebesuge积分的研究基础上严格拓展,并在模糊测度理论与应用中深化发展,成为模糊积分的一种。基于模糊测度的Choquet模糊积分有多种数学定义方式,在此如定义C.6、定义C.7所示。

定义C.6　设f:X→[0,+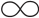),μ是定义在X上的模糊测度,f关于μ的Choquet模糊积分定义如下:

式中,Fα={x f(x)≥α,x∈X},X是一个有限集合。

当f:X→[0,1]时,Choquet模糊积分如定义C.7所示。

定义C.7　设有限集合X={x1,x2,…,xn},函数f为离散值函数,函数值分别为{f(x1),f(x2),…,f(xn)},且假设f(x1)≤f(x2)≤…≤f(xn),则f在X上关于测度μ的Choquet模糊积分模型[111,120]为

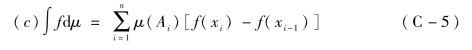
式中,f(x0)=0,Ai={ai,ai+1,…,an}。

对于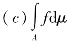有两种表示方式:

在此,μA是μ对A的限制。当f是非负时,式(C-6)和式(C-7)是相同的。

定理C.2　假设f和g是定义在X上的集合函数,A是X的子集,则(c)∫f dμ的性质如下:

①若μ是模糊测度,并且f≤g,则(c)∫f dμ≤(c)∫g dμ;

②若a是一个非负实数,b是一个实数,则(c)∫(af+b)dμ=a(c)∫dμ+bμ(X);

③(c)∫f dμ=(c)∫f+dμ-(c)∫f-dμ,其中,f+(x)=max{f(x),0},f-(x)=min{-f(x),0};

④若μ和v是定义在X上的模糊测度,μ≤v,那么对于在X上的所有函数f:(c)∫f dμ≤(c)∫f d v。

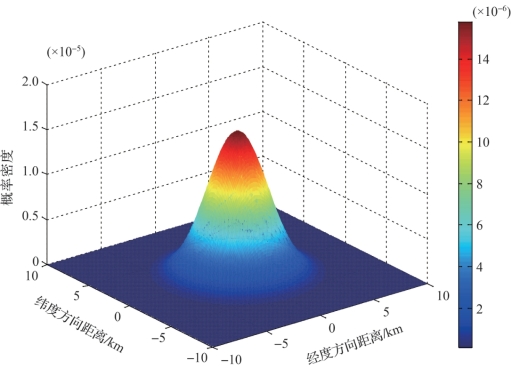
图2-5　应召搜潜时潜艇目标初始位置散布规律仿真图

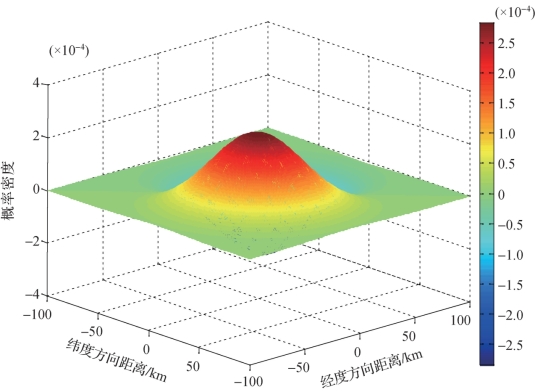
图2-6　速度未知条件下,潜艇位置概率密度分布示意图

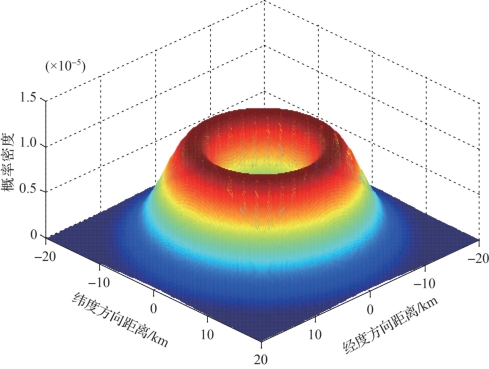
图2-7　速度已知条件下,潜艇位置概率密度分布示意图

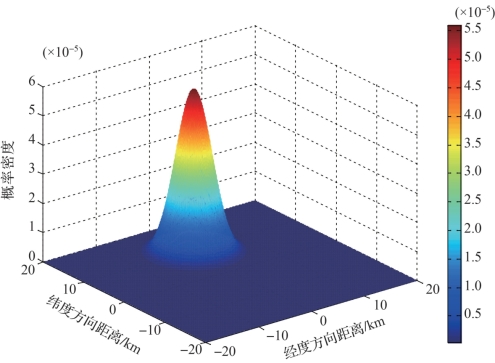
图2-8　已知潜艇速度和概略航向条件下,潜艇位置概率密度分布示意图

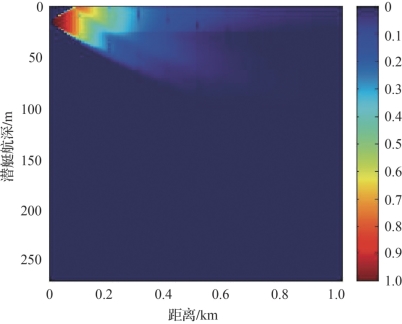
图4-25　工作深度15m时对极静型潜艇的瞬时探测概率

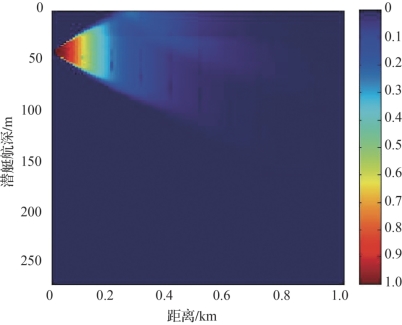
图4-26　工作深度40m时对极静型潜艇的瞬时探测概率

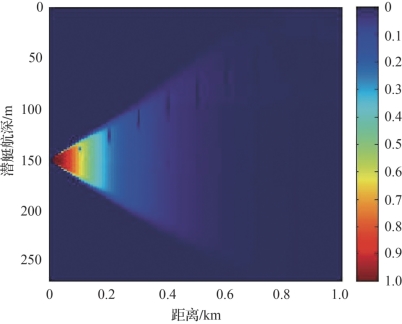
图4-27　工作深度150m时对极静型潜艇的瞬时探测概率

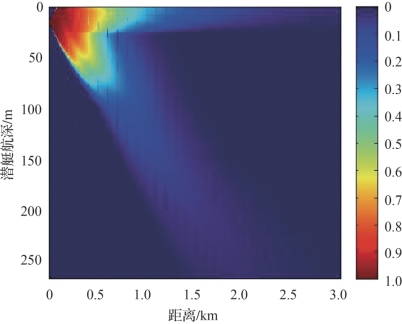
图4-28　工作深度15m时对静音潜艇的瞬时探测概率

图4-29　工作深度40m时对静音潜艇的瞬时探测概率

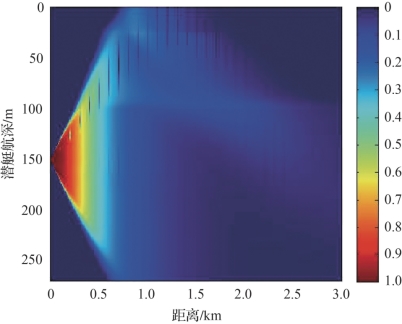
图4-30　工作深度150m时对静音潜艇的瞬时探测概率

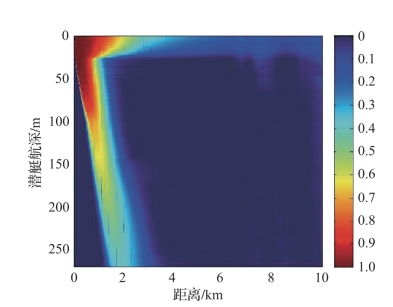
图4-31　工作深度15m时对噪声潜艇的瞬时探测概率

图4-32　工作深度40m时对噪声潜艇的瞬时探测概率

图4-33　工作深度150m时对噪声潜艇的瞬时探测概率

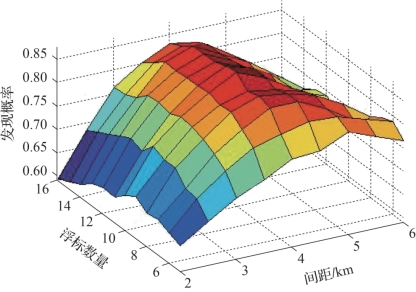
图4-37　圆形包围阵发现概率

图4-38　覆盖阵应召反潜发现概率

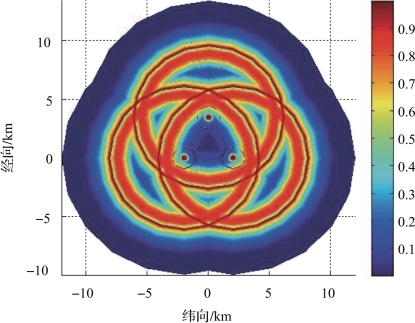
图4-41　对航深为45m敷瓦潜艇的瞬时探测概率覆盖范围

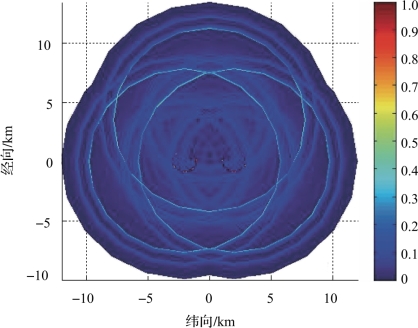
图4-42　对航深为150m敷瓦潜艇的瞬时探测概率覆盖范围

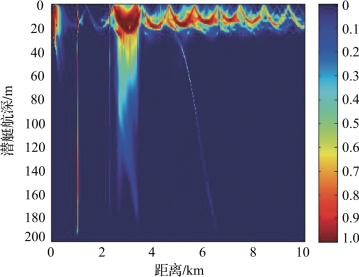
图4-43　工作深度15m时对敷瓦潜艇的瞬时探测概率

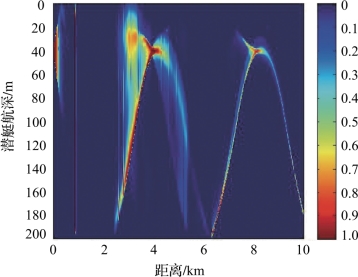
图4-44　工作深度40m时对敷瓦潜艇的瞬时探测概率

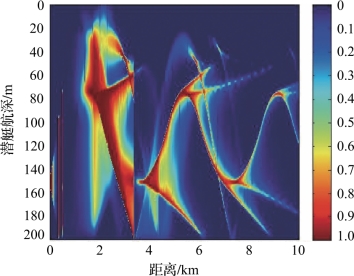
图4-45　工作深度150m时对敷瓦潜艇的瞬时探测概率

图4-46　工作深度15m时对未敷瓦潜艇的瞬时探测概率

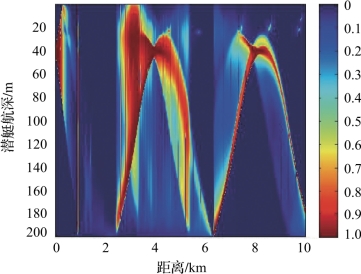
图4-47　工作深度40m时对未敷瓦潜艇的瞬时探测概率

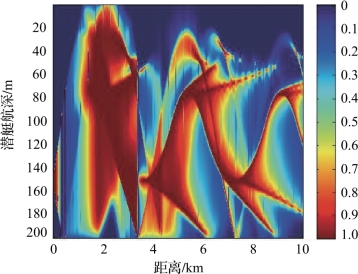
图4-48　工作深度150m时对未敷瓦潜艇的瞬时探测概率

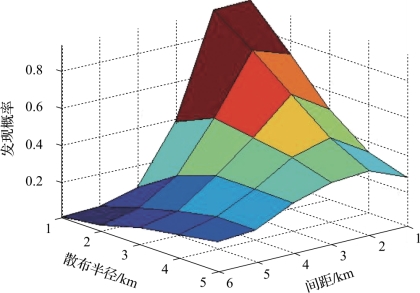
图4-51　三角阵对敷瓦潜艇的发现概率

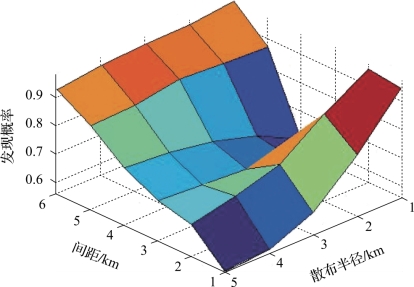
图4-52　三角阵对未敷瓦潜艇的发现概率

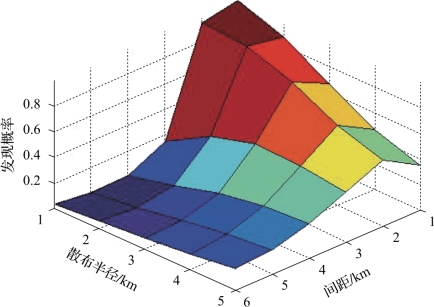
图4-53　十字阵对敷瓦潜艇的发现概率

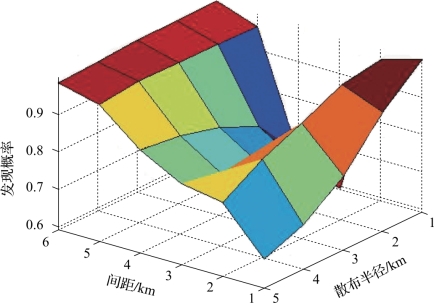
图4-54　十字阵对未敷瓦潜艇的发现概率