附录A 云模型理论
1.云和云滴
定义A.1 假设U是一个用精确数值量表示的定量论域,C是U上的定性概念。若定量值x∈U,且x是定性概念C的一次随机实现,x对C的确定度μ(x)∈[0,1]是具有稳定倾向的随机数,
![]()
则将x在论域U上的分布称为云,将每个x称为一个云滴,表示为drop(x,μ(x))。
云是由云滴组成的,一个云滴是定性概念在数量上的一次实现,云滴越多就越能反映该定性概念的整体特征。其中,云滴的确定度通常用模糊集理论中的隶属度概念来表示,反映了模糊性;同时,这个值自身也是一个随机值,可以用其概率分布函数描述。因此,云将模糊性和随机性有机地结合。
2.云的数字特征
云的数字特征反映了概念在整体上的定量特征[91-92],描述了云的形态分布。云有3个数字特征——期望(expected value)Ex、熵(entropy)En、超熵(hyper entropy)He,这3个数字特征共同决定了云图的分布。期望Ex是云滴在论域空间分布的期望,是云的重心位置,也是云滴最具代表性的数字特征,它在云图上表征为最高点,是最能代表定性概念的点,也是概念量化的最典型样本。熵En是云模型中用来衡量定性概念的模糊程度,其值的大小直接决定定性概念所涵盖的论域范围。熵值越大。则定性概念横跨的论域范围越大。超熵He是熵的不确定度量,即熵的熵,主要体现云滴的离散程度,表征为论域空间代表该语言值的所有点的不确定的凝聚度,反映为云形的厚度。超熵越大,云滴分布越离散,云层也就越厚。当超熵为0时,隶属云退化为模糊理论中的精确隶属度函数曲线。
3.云发生器
云的生成算法称为云发生器,所以在云模型中,定性概念与定量数值之间的转换是通过云发生器来实现的。云发生器按照功能来划分,可分为正向云发生器和逆向云发生器。
1)正向云发生器
正向云发生器(forward cloud generator,FCG)表示由定性概念到定量数值表示的过程(图A-1),是实现从定性概念到定量数据的转换模型,即定性到定量的映射。当云滴数是N时,其数值之间算法流程如图A-2所示。
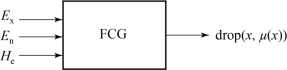
图A-1 正向云发生器示意图
正向云发生器的具体算法步骤如下:
第1步,生成一个以En为期望值、He为标准差的正态随机数E′n。
第2步,生成以Ex为数学期望值、E′n为均方差的随机数x。
第3步,令x为定性概念C的一次具体量化值,即(x,μ(x))。
第4步,计算x的确定度μ(x):
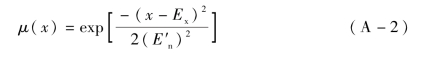
第5步,输出一个具有确定度μ(x)的云滴。
第6步,重复第1步~第5步,直至产生N个云滴。
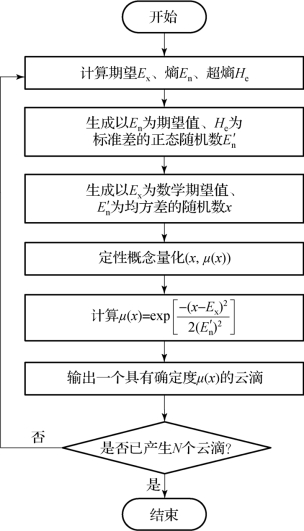
图A-2 正向云发生器算法流程示意图
2)逆向云发生器
逆向云发生器(backward cloud generator,BCG)表示由定量表示到定性概念的过程(图A-3),是实现定量数值到定性概念的转换模型,能够把精确的数据转换成用云模型数字特征(Ex,En,He)整体表示的定性概念,是基于云模型的连续数据离散化的一种方法,即从连续的定量数值区间到离散的定性概念的转换过程。BCG基本算法有两种,一种是利用确定度信息的逆向云算法,另一种是不需要确定度信息的逆向云算法。(https://www.daowen.com)
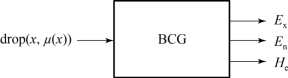
图A-3 逆向云发生器示意图
(1)基于确定度信息的逆向云算法流程如图A-4所示。
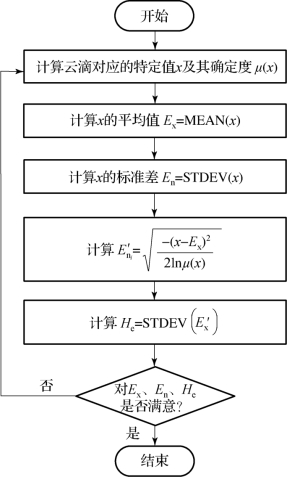
图A-4 基于确定度信息的逆向云发生器流程示意图
具体算法步骤如下:
第1步,计算x的平均值Ex=MEAN(x),求得期望Ex。
第2步,计算x的标准差En=STDEV(x),求得熵En。
第3步,对每一数对(x,μ(x)),计算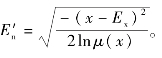
第4步,计算E′n的标准差He=STDEV(E′x),求得超熵He。其中,MAEN(·)和STDEV(·)分别是求平均值和标准差的函数。利用确定度信息的逆向云算法适用于数据值和确定度信息充足的情况。
(2)在确定度信息未知的情况下,采用的逆向云算法流程如图A-5所示。
该定量到定性的映射算法具体步骤如下:
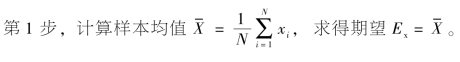
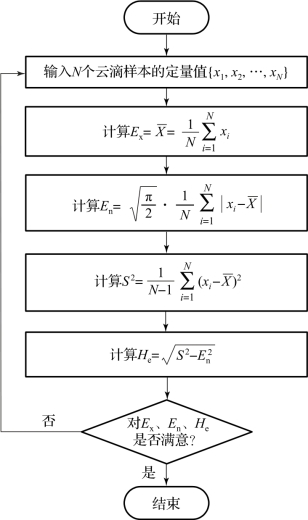
图A-5 不需要确定度信息的逆向云发生器流程示意图
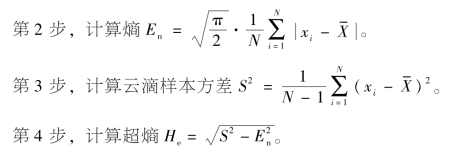
其中,xi(i=1,2,…,N)是N个云滴样本的定量值,云滴样本表示的定性概念有数字特征期望Ex、熵En、超熵He。
已知评估区间范围时,可采用指标近似法,即通过云模型进行表征定性语言值时,对于双边约束[Cmin,Cmax]的一些表达比较具有模糊性。可以选择下面的算法计算云参数[12]:
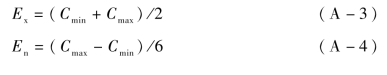
![]()
式中,k的取值可以根据实际场景中评估项所出现的可能情况作相应调整;熵En的度量方法服从3σ正态分布,即样本点的分布在判定区间中的概率为99.7%。当实际评估数据取到接近于阈值时,相对应的隶属程度也会趋近于0,此时样本点在边界区域的分布较为混乱,所以评估结果不易判断[12]。
4.云模型运算法则
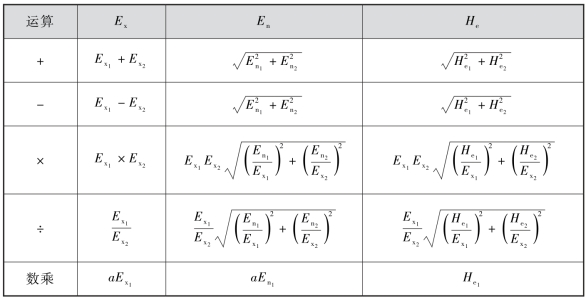
云模型之间有一定的运算规则,其四则运算法则以及与常数a的数乘运算法则如表A-1所示。
表A-1 云模型运算法则