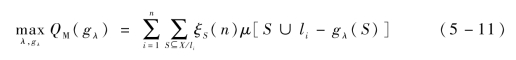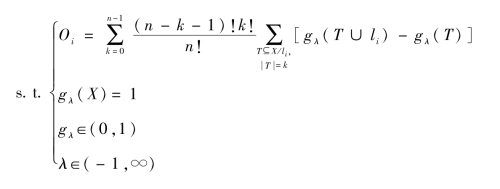5.3.3 模糊测度确定决策指标的重要性
模糊测度是经典测度的延续,不要求可加性的测度即模糊测度。模糊测度是描述事物重要程度的广义框架,可以更好地融合基本信息,有利于解决实际问题。1954年,法国数学家Choquet提出了关于容度的理论,这是最早对非可加性测度的系统研究。Choquet容度[109]是一种连续的且关于集合包含单调的集函数。在Choquet研究的启发下,由DemPster提出,后来经过Shafer深化,得出两种不同类型的非可加测度,即信任测度和似然测度。同时,DemPster和Shafer对信任测度和似然测度又进行了深入研究,进而形成了DemPster-Shafer理论或显著性理论[109]。然而,模糊测度理论的开创性工作是Zadeh在20世纪60年代后期完成的[92,110]。1974年,Sugeno在其博士论文中首次提出用较弱的单调性和连续性来代替可加性的另一类集函数,称为模糊测度[111](非可加测度)。模糊测度是对因素集的建模,可以表示一个(或多个)指标的综合重要程度,从而更加准确地刻画多个指标之间的相互关系[112]。
5.3.3.1 决策指标重要程度的模糊测度模型
模糊测度可以解决指标之间存在关联而又不具备可加性的多属性决策问题,基于模糊测度的指标重要性模型可以更准确地表示各指标的重要程度。搜潜能力、隐蔽性、可操作性和经济性作为反潜巡逻机协同搜潜决策的指标,不是各自孤立的,而是相互关联的。因此,引入gλ模糊测度描述反潜巡逻机协同搜潜决策的各指标重要程度。其定义如下:
定义5.1 设(X,F)为一可测空间,F为X的所有子集组成的σ-代数,g是F上的一个模糊测度,如果存在λ>-1,∀L,N⊆X,L∩N=∅,满足:
![]()
则称g为gλ模糊测度。若∀s∈X,则gλ(s)为属性集s的权重或重要程度;若λ=0,则说明各属性之间各自独立,相互没有关系;若-1<λ<0,则说明各属性之间冗余关联;若λ>0,则说明各属性之间互补关联;若X={x1,x2,…,xn}为有限集合,则映射:xi→gi=g({xi}),i=1,2,…,n,称为模糊密度函数。gλ模糊测度可完全由其模糊密度函数确定,即
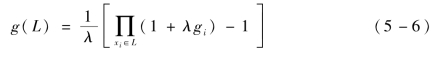
5.3.3.2 模糊测度的计算模型
gλ模糊测度的计算方法有很多,如Marichal熵算法、二次规划算法、神经网络算法、遗传算法都是常用的计算模糊测度的方法。其中,Marichal熵算法通过数据学习得到模糊测度,是一种比较客观的计算方法,在此采用Marichal熵算法。
1.计算指标的Shap ley值
Shapley值方法能够解决相关问题,是合作博弈中最重要的收益指标之一,它以严格的公理为基础,满足有效性公理、对称性公理、可加性公理,在处理合作对策的分配问题时具有公正、合理等优点。采用模糊测度对反潜巡逻机协同搜潜决策指标的权重建模时,由于指标间的不可加性,所以指标权重由Shapley值取代,用以描述决策指标在决策中的综合贡献。因此,在求解指标(集)权重之前,应确定常权情形下指标的Shapley值。根据多人博弈中Shap ley函数[113]的定义,以及Grabisch[114]对广义Shapley函数的定义,基于gλ模糊测度的Shap ley值计算如下:
若∀li∈X,gλ为定义在X上的模糊测度,那么基于gλ模糊测度的Shapley值Oi表示为(https://www.daowen.com)
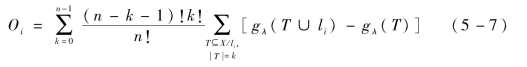
式中,n——X中元素个数;
k——T的基数;
Oi——属性li在整个指标集中的贡献,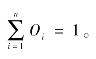
2.M arichal熵计算模糊测度
Marichal熵算法采用构建优化模型,通过最大化Marichal熵来计算实现指标和指标集的重要程度,即指标和指标集的模糊测度。具体如下:
定义5.2 设X为指标集,n为X中元素的个数,gλ为定义在X上的模糊测度,则Marichal熵为
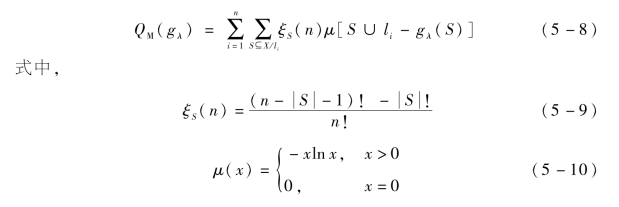
依据不同状态下决策指标的Shapley值、Marichal熵和gλ模糊测度的定义和性质,以Marichal熵最大为目标函数,依据优化模型(式(5-8))求解各指标的模糊测度: