5.3.4 Choquet模糊积分确定决策结果
2026年01月16日
5.3.4 Choquet模糊积分确定决策结果
模糊积分的理论研究由来已久,García、Álvarez、吴从炘等学者对模糊积分的发展进行了研究[115-117]。近年来,模糊积分得到迅猛发展。Choquet模糊积分是法国数学家Choquet针对他提出的Choquet容度定义的一种积分,因为模糊测度与容度的相似性以及Choquet积分的单调性,就把关于模糊测度的Choquet积分看作一种模糊积分,现被广泛称为Choquet模糊积分[118-119]。当模糊测度有经典的可加性时,Choquet积分就退化为Lebesuge积分[120],所以,Choquet积分是Lebesuge积分的推广。早在1989年,Murofushi和Sugeno就把Choquet积分和模糊测度联系起来研究,可以说,正是模糊测度的发展带给了Choquet积分新的生命力。随着Murofushi与Sugeno等人后续在模糊测度上的研究和对Choquet模糊积分的改进,其得以在传统Lebesuge积分的研究基础上严格拓展,并在模糊测度理论与应用中深化发展,成为模糊积分的一种。
采用模糊测度对指标(集)的重要性建模时,决策指标(集)的集成计算(即相关指标(集)的集结算子)通常采用Choquet模糊积分。对决策方案集合X={x1,x2,…,xn},ρ是定义在X上的模糊测度,函数f(·)为归一化的离散值指标函数,函数值集合为{f(x1),f(x2),…,f(xn)},且假设f(x1)≤f(x2)≤…≤f(xn),则反潜巡逻机协同搜潜指标集成计算如下:
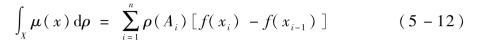 (https://www.daowen.com)
(https://www.daowen.com)
式中,f(x0)=0,Ai={xi,xi+1,…,xn}。
运用Choquet模糊积分集结各指标函数后,所得结果即方案的最终优势排序,从而选出最优或近似最优方案。
