附录B　贝叶斯网络

附录B　贝叶斯网络

1.贝叶斯网络基本概念

1985年,Judea Pearl首先提出贝叶斯网络(Bayesian network,BN),亦称信念网络、信度网络、因果网络,是贝叶斯方法的扩展,是一种基于概率分析和图论的不确定性知识的表达和推理模型。贝叶斯网络采用网络描述事件和假想之间的相互关系,以条件概率描述节点之间的关联程度。贝叶斯网络以表示因果关系的有向无环图来表示。图中的节点表示变量或事件,有向边表示变量之间的依赖关系,这种关系用条件概率P表示。贝叶斯网络的节点变量既可以是离散型,也可以是连续型。有向边出发的节点称为双亲节点,到达的节点称为孩子节点。孩子节点依赖于双亲节点。一旦双亲节点的状态确定,孩子节点的状态也就确定。贝叶斯网络规定:对于任意一个节点,在给定该节点的直接父节点条件下,该节点与任意除该节点及其后代节点以及直接父节点以外的其他节点条件独立。图B-1所示为一个简单的贝叶斯网络,A是双亲节点。B、D和E是孩子节点。C是A的孩子节点,且是D和E的双亲节点。节点变量可以是任何问题的抽象,如测试值、观测现象等。每一个节点都附有与该变量相联系的条件概率分布函数,如果变量是离散的,则它表现为给定其父节点状态时该节点取不同值的条件概率表(根节点的条件概率用其先验概率表示)。

图B-1　贝叶斯网络

如果一个节点的状态是可以观测的,则该节点称为可观测节点;否则称为隐藏节点。离散静态贝叶斯网络的一个重要性质就是条件无关性,即在给定双亲情况下,孩子节点的状态与其他节点无关。

贝叶斯网络能够以图形的模式直观描述变量之间的概率关系,是一种将概率论和图论完美结合、可用于不确定事件分析和推理的工具,其最显著的特点是直观、准确,其特性有条件独立性、基于概率论的严格推理、知识表示。

1)条件独立性

贝叶斯网络求某个变量概率信息时,只考虑与该变量有关的变量,从而大大降低了问题的复杂度。

2)基于概率论的严格推理

贝叶斯网络是不确定性知识表达和推理模型,它的推理原理就是贝叶斯概率论。

3)知识表示

贝叶斯网络知识表示分为定性知识表示和定量关系表示。定性知识是指网络结构表示的事件之间的因果关系;定量关系是指节点的条件概率表,主要来源于专家经验等途径。

2.贝叶斯网络参数和结构的学习

一个贝叶斯网络由两部分构成——网络结构S、节点X的条件概率P。S是一个有向图,每个节点代表一个数据变量Xi,Pai为S中节点Xi的父节点集合。条件概率P中每个元素为数据变量Xi的条件概率密度ζ为观测者的先验知识,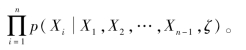对于任一数据变量Xi,必可找到一个与Xi条件都不独立的最小子集πi∈{X1,X2,…,Xi-1},使得此时πi中的变量就是贝叶斯网络中Xi的父节点Pai,故

贝叶斯网络的学习[13]就是找出一个能够真实反映数据库中的数据和变量之间关系的网络结构。记变量集X={X1,X2,…,Xn},对于每一个变量Xi,其值域为为数据样本集,S h为网络结构S所产生的事件。贝叶斯网络的学习过程也就是根据数据样本D和先验知识ζ找出后验概率最大的贝叶斯网络结构S的过程。由贝叶斯概率公式可知,样本D的先验概率不依赖于网络的结构S。记先验概率的参数变量θijk=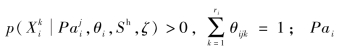的值域为为Pai的所有的状态,则

对于贝叶斯网络的学习,有以下3个假设条件[94]:

(1)随机样本D是完整的,即D中没有丢失的数据。

(2)参数变量相互独立,即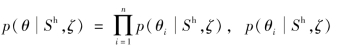为第i个变量χi的先验概率密度,为变量xi的父节点为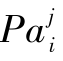时的先验概率密度。

(3)参数变量Dirichlet分布,即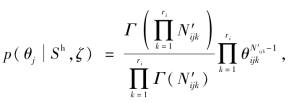其中N′ijk＞0为Dirichlet分布的指系数,它的大小与S h和ζ有关,当ri=2时,Dirichlet分布即β分布。最后可得

式中,Nijk——数据库中满足且父节点状态组合为j的样本数;

此时联合概率只由Dirichlet分布的指系数N′ijk决定,这表明,贝叶斯网络的学习过程即寻找指系数N′ijk,使联合概率最大。

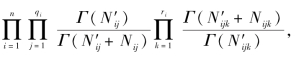记g(Xi)=则,g(Xi)为数据变量Xi对联合概率密度的贡献值,每个g(Xi)是独立的,我们对每个Xi逐个计算,找出能使g(Xi)增大的数据变量Xi,直到g(Xi)不再增加,找到的这些g(Xi)就为Xi的父节点。

3.贝叶斯网络推理

贝叶斯网络推理是指利用贝叶斯网络的结构及其条件概率表,在给定证据后,计算某些节点取值的概率。它是在一个不确定环境和不完全信息下进行决策支持和因果发现的工具。贝叶斯推理提供了一种以概率为基础的推理算法,它针对人们感兴趣的并受概率控制的变量,结合观察到的数据,对这些概率进行推理并做出最优的决策。贝叶斯网络推理提供了一种通过加权证据支持可用假设的定量方法,这不仅为那些直接操纵概率的算法提供了理论基础,而且为分析未明确运算概率的算法提供了理论构架。

贝叶斯网络的推理算法分为精确算法和近似算法。常用的贝叶斯网络的精确推理算法有桶消元法、连接树算法、信息传递算法。其中,连接树算法(junction tree algorithm)是应用最为广泛和计算速度最快的方法。该算法首先把贝叶斯网络转化为一个连接树,将联合概率分解为局部概率的因式形式,以此减小联合概率的计算量;然后,通过连接树上节点之间的消息传递来进行计算,消息会依次传遍整个连接树,直到连接树满足全局一致性。对变量进行消除、道义化及三角化后,就形成一个删除树[95](elimination trees);删除的节点满足运行交叉属性(running intersection property,RIP)后,便可以从中构造一个连接树。RIP是指一个有序的集合序列C1,C2,…,Ck,对所有的1＜j≤k,存在一个i＜j,使得Cj∩(C1∪C2∪…∪Cj-1)⊆Ci。

Pearl提出的算法在贝叶斯网络的推理中也应用较广泛,其基本思想是:为每个节点分配一个处理器,每个节点既可以发送证据(distribute evidence)也可以收集证据(collect evidence)。因此,经过这样的过程后,每个节点的信度就会发生改变从而得到更新。如图B-2所示,在一个简单的贝叶斯网络中,子节点与父节点之间存在一个固有的概率关系(称为先验概率),这个关系不会因为节点信度的改变而发生变化。在推理过程中存在两种信息形式:从子节点传来的诊断信息λ;父节点向子节点发送的因果信息π。当节点得到这两种信息后,就可以更新自身的信度。以节点M为例,其诊断信息λ(M)=λM(R)×λM(F),其因果信息π(M)=πM(S)×其中为节点S和节点M之间的条件先验概率,以及的含义同理,故此时节点M的信度为BEL(M)=λ(M)×π(M)。

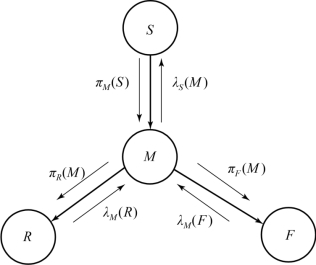
图B-2　贝叶斯网络信息传递图

贝叶斯网络推理的依据就是贝叶斯公式:

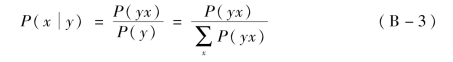
对一个具有n个隐藏节点和m个观测节点的离散静态贝叶斯网络应用贝叶斯网络的条件独立特性[96],得到其推理公式为

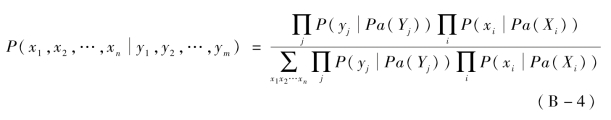
式中,i∈[1,n],j∈[1,m];xi表示隐藏节点Xi的一个取值状态;yj表示观测节点Yj的取值;Pa(Yj)表示观测节点Yj的双亲节点集合;分母求和符号∑下的x1 x2…xn为隐藏变量的一种组合状态。式(B-4)分母的含义是对观测变量组合状态和隐藏变量组合状态的联合分布求和,实际是计算确定的观测变量组合状态的分布。