6.3　基于贝叶斯粗糙集与模糊理论的智能决策方法研究思路

双/多反潜巡逻机自主模式协同搜潜作战过程中,进行协同搜潜发挥最大效能,选出最优决策方案,需要考虑很多因素。对应不同的潜艇状态和战场态势、水文环境条件,每一种搜潜行动方案都有其自身的特点。因此,需要根据反潜巡逻机协同搜潜作战的特点,基于海洋战场环境和目标潜艇出现状态的不确定性及搜索设备的不同特点,通常从搜索能力、成本、隐蔽性和实施难度等方面综合选取决策指标。但在建立决策指标模型时,有些指标的属性值很难得到或者测量这些属性值的代价很高,就需要将这些指标从决策表中去掉,得到尽可能最少的决策规则;而且,不可能建立包括所有影响决策结果的参数方程体系,应该选择尽可能少的参数或选择参数的某种组合来建立模型。粗糙集仅利用数据本身提供的信息,无须任何先验的专家知识,可以从决策系统的指标中去掉不必要(或不重要)的指标,因而在实际决策中得到较广泛的应用。但是经典的粗糙集在处理分类关系时过于严格,容易将有用的信息也剔除,不利于决策分析。贝叶斯粗糙集在判断集合间的隶属关系时,引入了一个不确定度,能够更好地描述集合间的依赖关系,可以弥补经典粗糙集的不足,而且贝叶斯粗糙集不需要任何预备或额外的有关数据信息。贝叶斯粗糙集的属性简约方法[126-128]可以在保持知识库分类能力不变的条件下,删除其中不相关(或不重要)的知识,即可以从决策表系统的指标中去掉不必要(或不重要)的指标,在去除冗余数据的同时,可以提高算法的速度,从而可以更高效、快速地解决反潜巡逻机协同搜潜作战决策过程中指标的冗余问题。因此,本章引入贝叶斯粗糙集指标简约算法,挑选关键特征参数,解决决策指标冗余问题。

指标依赖度表示两个指标集合之间的相互依赖程度,指标重要度表示不同指标对于条件指标和决策指标之间的相互依赖关系起着不同的作用。在剔除决策冗余指标的过程中,指标依赖度和指标重要度的计算方法是确保整个算法有效、可行的关键环节。

因此,基于贝叶斯粗糙集和模糊测度、模糊积分构建反潜巡逻机协同搜潜作战智能决策模型,首先确定相关的决策指标,将决策问题转换为组合优化求最优的问题,再结合贝叶斯粗糙集、模糊测度、模糊积分理论,求解反潜巡逻机协同搜潜作战智能决策问题。在求解过程中,可以通过贝叶斯粗糙集的知识简约从决策表系统的指标中去掉不必要(或不重要)的指标,以提高算法的收敛速度。另外,在综合决策指标过程中,每个决策指标设置的加权系数会直接影响决策的效果,而且有些决策指标是相互依赖、相互矛盾的,所以引入模糊测度。模糊测度是对指标集的建模,可以表示一个或多个指标的综合重要程度。相对其他计算方法,模糊测度能更加准确地刻画多个指标之间的相互关系,而且设置加权系数被计算Shap ley值取代,从而可以公正、合理地分配决策指标权重,使其更符合实际作战的情况,可以用来解决反潜巡逻机协同搜潜作战决策过程中指标的相互关联问题。具体研究思路如图6-1所示。

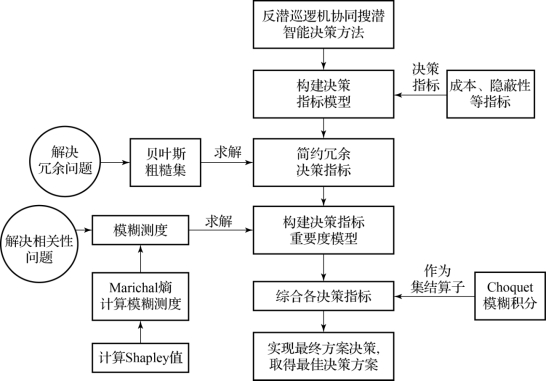
图6-1　反潜巡逻机协同搜潜智能决策方法研究思路示意图