4.3.1 云的数字特征对云图影响分析
云模型[90]是李德毅院士于1995年在概率论和模糊数学理论两者交互的基础上提出的一种不确定关系的转换模型。云模型从自然语言的基本语言单位入手,对定性概念进行一种量化的定义,从而使得自然语言中的定性概念和其对应的定量数值之间能够进行不确定性转换,表达了自然语言的不确定性属性。解决模糊性问题通常采用模糊数学理论,解决随机性问题通常采用概率论,而云模型通过特定的结构算法,将模糊性与随机性的概念较为有效地融合,组成定量与定性之间的映射,能够兼顾模糊性和随机性,从而很好地表达数据的不确定性以及专家知识,比模糊集理论更胜一筹。
云有3个数字特征:期望(expected value)Ex、熵(entropy)En、超熵(hyper entropy)He。云的数字特征反映了概念在整体上的定量特征[91-92],共同决定了云的形态分布。正态云是最重要的一种云模型,它具有普适性。在此以正态云为例,分析其数字特征对云图的影响,取不同参数的正态云模型进行MATLAB仿真。
(1)Ex=18,En=2,He=0.2,云滴数N=1 000时,仿真云图如图4-1所示。
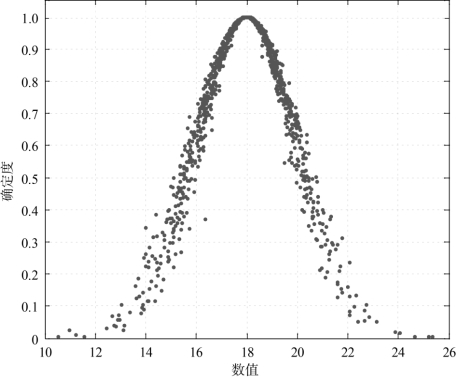
图4-1 Ex=18,En=2,He=0.2,N=1 000,正态云图
(2)Ex=18,En=2,He=0.2,云滴数N=3 000时,仿真云图如图4-2所示。
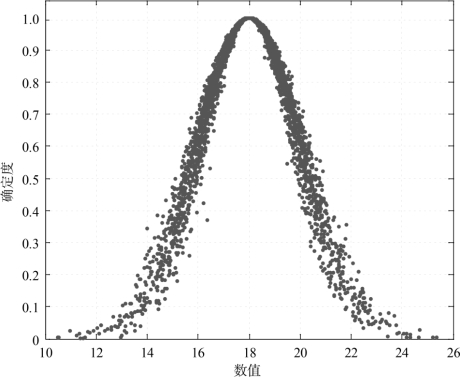
图4-2 Ex=18,En=2,He=0.2,N=3 000,正态云图
(3)Ex=28,En=2,He=0.2,云滴数N=3 000时,仿真云图如图4-3所示。
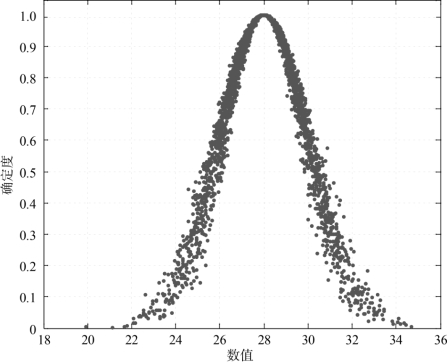
图4-3 Ex=28,En=2,He=0.2,N=3 000,正态云图
(4)Ex=0,En=2,He=0.2,云滴数N=3 000时,仿真云图如图4-4所示。
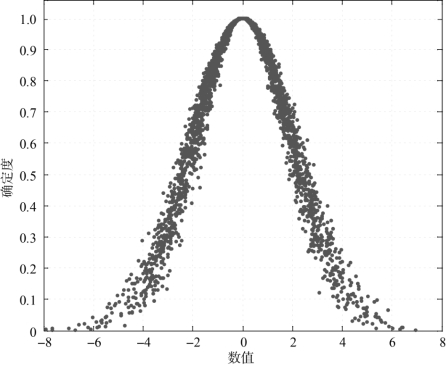
图4-4 Ex=0,En=2,He=0.2,N=3 000,正态云图(https://www.daowen.com)
(5)Ex=0,En=1,He=0.2,云滴数N=3 000时,仿真云图如图4-5所示。
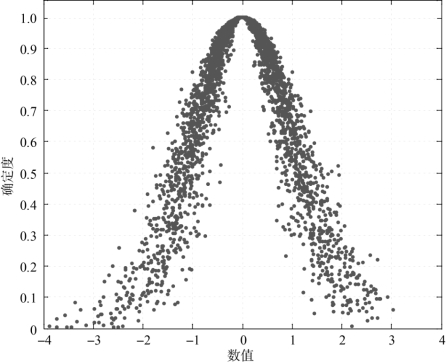
图4-5 Ex=0,En=1,He=0.2,N=3 000,正态云图
(6)Ex=0,En=0.5,He=0.2,云滴数N=3 000时,仿真云图如图4-6所示。
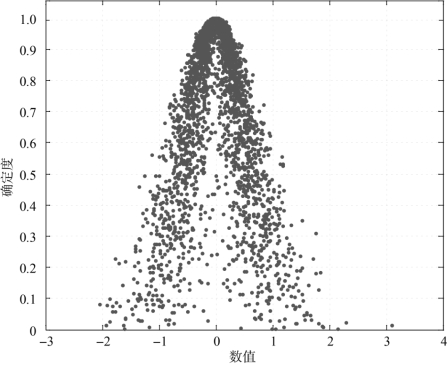
图4-6 Ex=0,En=0.5,He=0.2,N=3 000,正态云图
(7)Ex=0,En=1,He=0.1,云滴数N=3 000时,仿真云图如图4-7所示。
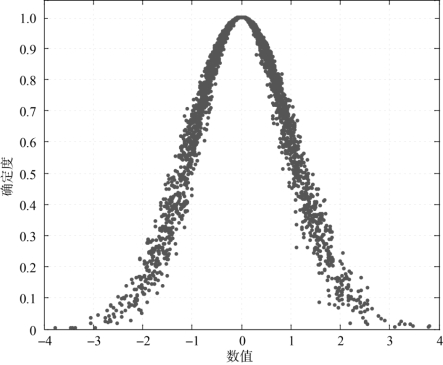
图4-7 Ex=0,En=1,He=0.1,N=3 000,正态云图
(8)Ex=0,En=0.5,He=0.1,云滴数N=3 000时,仿真云图如图4-8所示。

图4-8 Ex=0,En=0.5,He=0.1,N=3 000,正态云图
由上述仿真云图可以看出,熵反映了云滴在论域中的离散程度,超熵反映了云层的厚度和离散度。熵越大,云滴分布范围越大;反之,云滴的分布范围就会越小。超熵越小,云层就越薄、越集中;反之,超熵越大,云层就越厚、越离散。
