6.4.1 简约决策指标
反潜巡逻机协同搜潜过程中,获得的数据信息往往具有不完全性和不确定性,遇到不完整信息时,尽可能给出问题的最大可能解往往具有很大的实际意义。贝叶斯粗糙集模型[128]用事件发生的先验概率代替变精度粗糙集中的精度参数β,既可以克服粗糙集模型的完全精确划分的困难,又可以避免变精度粗糙集模型需要预先给定参数,是基于变精度和概率论的无参数模型。贝叶斯粗糙集的简约方法有多种,在此利用全局增益函数来求简约,假设信息系统S=(U,C∪D,V,f),U是对象的非空有限集合,C是条件指标集,D是决策指标集,V=∪Va,a∈C∪D,Va是指标a的值域,f是信息函数。对E⊆C,U/D={X1,X2,…,Xr},则称
![]()
为E相对于决策指标D的全局相对增益函数[128]。
假设X和E是等价关系,a∈E,如果RE-{a}(X)=RE(X),则称a为E中X不必要的,否则a为E中X必要的。E中所有X必要的集合称为E的X核[128]。
对于∀X⊆U,子集B⊆C,则称B为X的R简约[128],且满足RB(X)=RC(X),并且去掉B中的任意一个指标都会使该等式不成立。
综上,假设Core(C)是条件指标的核指标集合,RC(D)是每个指标的全局相对增益函数值,Rrc(D)是Core(C)相对决策指标D的全局相对增益函数值,对于∀Ci∈C,RCi(D)是Ci相对决策指标D的全局相对增益函数值,则贝叶斯粗糙集指标简约算法的具体思路如图6-2所示。
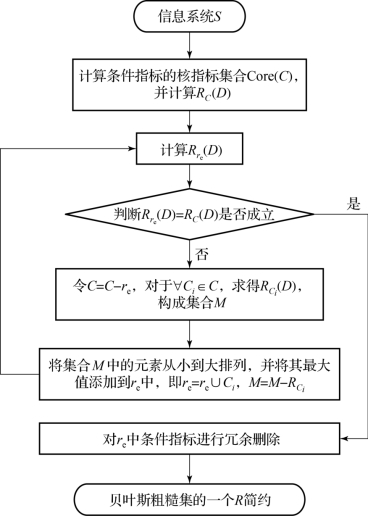
图6-2 贝叶斯粗糙集指标简约算法流程(https://www.daowen.com)
该算法编程实现的基本思路:首先,把决策表条件指标的各种组合编成二进制编码;其次,把所有编码组合对应的指标集、条件指标分别相对于决策指标的分类质量进行比较,如果相等则将该指标集作为矩阵的一行;再次,根据准则,对子集已经是简约的行进行删除,并删除全为零的行;最后,计算所有R简约,并组成矩阵,即得到所有R简约。具体步骤如下:
第1步,假设n=2m-1,M是矩阵n×m的零矩阵,并且假设j=2m-1。
第2步,对j进行二进制编码,每个二进制编码中1所对应的指标组合是P,根据P(X)用轮盘赌的形式从大到小依次计算P的全局相对增益函数值RP(X)。
第3步,如果RP(X)=PC(X)成立,则用P所对应的二进制编码替换M中的第j行,否则继续运算。
第4步,执行j=j-1,如果j≥1,则返回第2步,否则继续。
第5步,根据准则,删除M中冗余的行,并删除全为零的行。剩余的行对应的指标集即贝叶斯粗糙集的所有指标简约。
第6步,计算出核。
该算法的时间复杂度为![]()
