现代化经济体系评价指标体系的构建逻辑
基于大量文献研究，在相关学者的研究基础上，本研究将现代化经济体系与新发展理念对照结合，把现代化经济体系解构为八个子体系，主要从这八个方面对现代化经济体系评价指标体系进行构建，具体指标的选择根据八个子体系的具体特征进行选择。在总结相关学者的大量研究基础上，本研究将创新体系的现代化特征概括为：创新动力不断增强、创新水平逐渐提升、创新人才培育体系逐渐成熟。市场体系的现代化特征包括市场准入畅通、开放有序、竞争充分、秩序规范、商品和要素自由流动等；经济体制现代化的特征包括市场机制有效、微观主体有活力、宏观调控有度等，具体包括经济增长、物价稳定、就业稳定；产业体系的现代化特征包括科技创新对实体经济的贡献份额不断提高、现代金融服务实体经济的能力不断增强、人力资源支撑实体经济发展的作用不断优化、三大产业结构合理且服务业占国内生产总值（GDP）的比重不断提升；绿色发展体系的现代化特征包括绿色循环低碳、人与自然和谐发展、资源节约、环境友好、环境治理能力稳步上升；共享发展体系的现代化特征包括人均GDP逐步提高、全体人民共同富裕、收入分配差距合理、贫富差距缩小、基本公共服务均等化；城乡区域发展体系的现代化特征包括城乡居民可支配收入日趋合理、区域优势互补、城乡融合发展和陆海统筹整体优化；全面开放体系的现代化特征包括结构优化、合作深化和效益提高。
本研究将现代化经济体系解析成一个有序的递阶层次结构，其指标体系分为8个目标层、29个准则层和40个指标层。
目标层反映现代化经济体系中创新体系、市场体系、经济体制、产业体系、绿色发展体系、共享发展体系、城乡区域发展体系和全面开放体系的整体发展水平，其中创新体系构成现代化经济体系的动力系统，市场体系和经济体制构成现代化经济体系的传动系统，产业体系、绿色发展体系、共享发展体系、城乡区域发展体系和全面开放体系构成现代化经济体系的运行质量系统。
准则层是对8个目标层的进一步分解，反映其具体内容或特征，例如创新体系可以分解为创新动力发展、创新水平提升和创新人才培养；市场体系可以分解为政商和谐、市场竞争充分和市场环境良好；绿色发展体系可以分解为资源节约、环境友好和环境治理能力改善等。
指标层反映现代化经济体系各子体系的具体发展水平，是本研究构建现代化经济体系评价指标体系的关键，它能有效衡量经济体系现代化的动态变化趋势。本研究将新发展理念融入现代化经济体系评价指标体系的构建当中是一大特色和创新，充分体现了指标选择的系统性和科学性，各目标层体系之间通过指标层传达出较强的逻辑联系。例如：对于创新体系和产业体系的逻辑联系，创新体系中的计算机、信息及软件业固定资产投资强度既能衡量创新动力发展，也体现了产业体系的转型升级；而产业体系中的产品质量优等品率则体现技术创新在产业朝着微笑曲线两端提升过程中的重要作用。现代化经济体系评价指标体系的构建充分结合系统性、科学性、可量化性、简明性和动态性的指标构建原则，吸取现代化经济体系的具体内核，融合创新、协调、绿色、开放、共享五大新发展理念的核心观念，构建了一套系统全面、简明有效、科学合理、动静结合的指标体系，力求准确充分地反映现代化经济体系的发展水平和变化。
在指标层级及指标体系确定的条件下，本研究将进一步对各项指标采用层次分析法来赋权。层次分析法（analytic hierarchy process，AHP）是一种将定性与定量指标相结合的决策分析方法，是一种将复杂问题分解成各个组成因素，再将这些因素按照支配关系分组形成递阶层次结构，以两两比较的方式确定各个因素的相对重要性，通过求解相对重要性判断矩阵来确定权重的方法。层次分析法的基本思路是将所要分析的问题层次化，根据问题的性质和所要达成的总目标，将问题分解为不同的组成因素，并按照这些因素的关联影响及其隶属关系，将因素按不同层次凝聚、组合，形成一个多层次分析结构模型，最后对问题进行优劣比较并排列。
第一步，建立层次结构模型。将决策的目标、考虑的因素（决策准则）和决策对象按照它们之间的相互关系分为最高层（目标层）、中间层（准则层）和最低层（指标层），绘出层次结构图。其中最高层（目标层）是决策的目的、要解决的问题；中间层（准则层）是决策要考虑的因素、决策的准则；最低层（指标层）是决策时的具体指标。层次分析法所要解决的问题是关于最低层对最高层的相对权重问题，按此相对权重可以对最低层中的各种方案、措施进行排序，从而在不同的方案中作出选择或形成选择方案的原则。
第二步，构造判断矩阵。对同一层次的各个指标关于上一层次中某一准则的重要性进行两两比较，构造两两比较的判断矩阵（通常需要结合专家经验对指标的两两相对重要性作出判断）。层次分析法中构造判断矩阵的方法是一致矩阵法，即不把所有因素放在一起比较，而是两两相互比较；此时采用的是相对尺度，尽可能减少性质不同因素相互比较的困难，以提高准确度，如表3-1所示。
表3-1 判断矩阵标度方法
第三步，求解判断矩阵的特征向量（各指标的相对权重），并对层次排序做一致性检验。各指标的相对权重计算公式如下：
（1）计算每个指标的几何平均数：
，其中ai，j为判断矩阵的元素。
（2）标准化处理：多指标评价体系中，由于各评价指标的性质不同，通常具有不同的量纲和数量级。指标的标准化（normalization）是将数据按比例缩放，使之落入一个小的特定区间。在某些比较和评价的指标处理中经常会用到，去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行比较和加权。当各指标间的水平相差很大时，如果直接用原始指标值进行分析，就会突出数值较高的指标在综合分析中的作用，相对削弱数值水平较低指标的作用。因此，为了保证结果的可靠性，需要对原始指标数据进行标准化处理。目前数据标准化方法有多种，归结起来可以分为直线型方法（如极值法、标准差法）、折线型方法（如三折线法）、曲线型方法（如半正态性分布）。其中最典型的就是数据的归一化处理，即将数据统一映射到[0，1]区间上，常见的数据归一化的方法有：min-max标准化法（min-max normalization）、log函数转换法、atan函数转换法、Z标准化因子得分法（此方法最为常用）、模糊量化法。在指标标准化处理中，W i=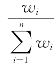
，其中Wi是每个指标的相对权重。
（3）一致性检验：构建一个正互反矩阵列A，当A满足aijajk=aik，i、j、k=1，2，3，…，n时，A为一致性矩阵。检验上述第二步构造的矩阵是否与一致性矩阵有太大差别，如果差距太大则一致性检验不通过，需要重新构建判断矩阵，直至通过一致性检验为止。
最后，进行层次总排序的一致性检验。计算某一层次所有因素对于最高层（总目标）相对重要性的权值，称为层次总排序。这一过程是从最高层次到最低层次依次进行的。若A层有m个因素：A 1，A2，…，Am，其对总目标Z的权重分别为W1，W2，…，Wm；B层有n个因素对上层A中因素Aj的层次，单权重为b1，j，b2，j，…，bm，j（j=1，2，…，m），B层的层次总权重为：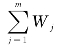
·bij。层次总权重的一致性比率为
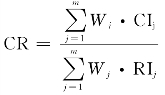，当CR＜0.1时，层次总权重一致性检验通过。