指标的权重设置
1.建立层次结构模型
根据现代化经济体系评价指标体系建立层次分析结构模型,如表3-3所示。目标层为现代化经济体系,准则层为8个子体系(对应的矩阵为A1~A7),方案层为各具体指标(标度为B1~B40)。
表3-3 AHP层次结构
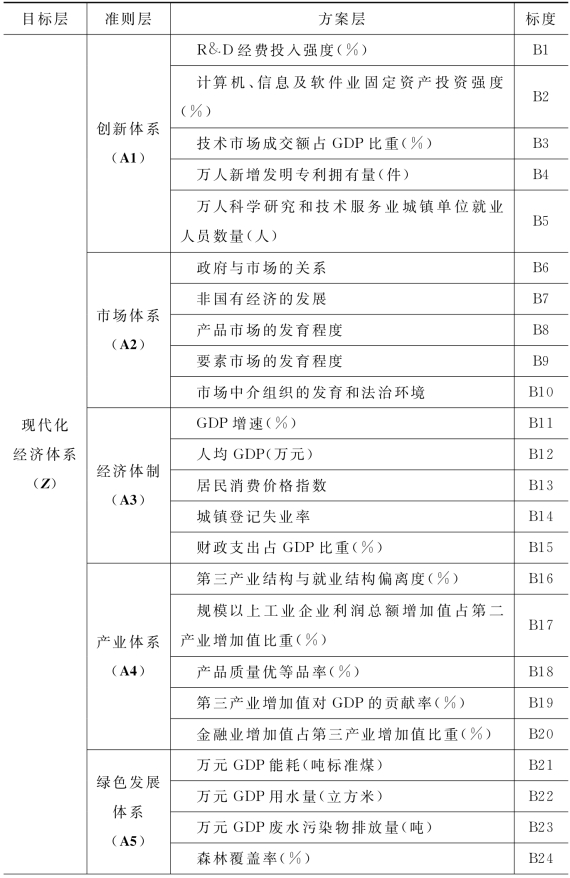
续表
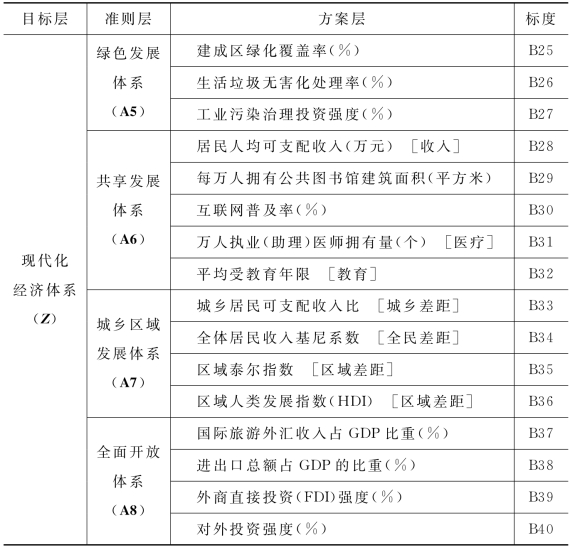
2.构建判断(成对比较)矩阵
为了消除完全主观因素的误差,采用Santy等人提出的一致矩阵法构建判断矩阵对准则层指标和方案层指标进行赋权。这样做的好处是通过两两比较,采用相对尺度,尽可能减少性质不同的诸因素相互比较的困难,以提高计算的精确性。成对比较矩阵是表示本层所有因素针对上一层某一个因素(准则或目标)相对重要性的比较。成对比较矩阵的元素aij表示的是第i个因素相对于第j个因素的比较结果,aji表示aij的倒数,这个值是使用Santy 1~9标度方法给出的(具体方法见表3-1)。
根据现代化经济体系指标体系的递阶层次结构,按照1~9标度规则构建判断矩阵,共构建了9个判断矩阵(分别为1个准则层对目标层的判断矩阵和8个方案层对准则层的判断矩阵),如表3-4至表3-11所示。
表3-4 A对Z的判断矩阵
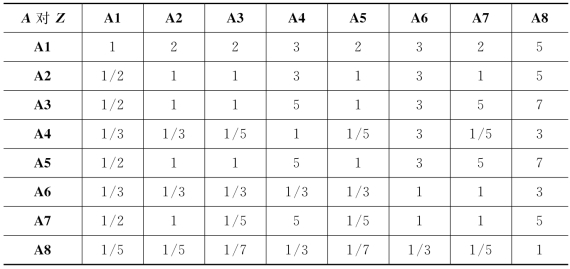
WZ=(0.226,0.141,0.191,0.065,0.191,0.059,0.103,0.026)T
分别为表3-1中8个体系的权重。
表3-5 B1~B5对A1的判断矩阵
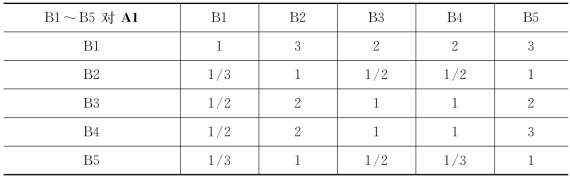
W A1=(0.364,0.108,0.203,0.223,0.101)T
表3-6 B6~B10对A2的判断矩阵

续表
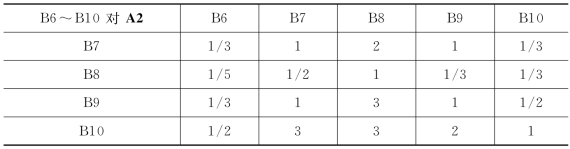
WA2=(0.404,0.124,0.068,0.146,0.258)T
表3-7 B11~B15对A3的判断矩阵
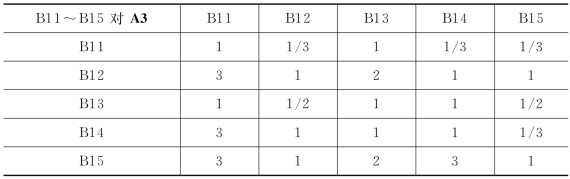
WA3=(0.096,0.259,0.136,0.188,0.322)T
表3-8 B16~B20对A4的判断矩阵
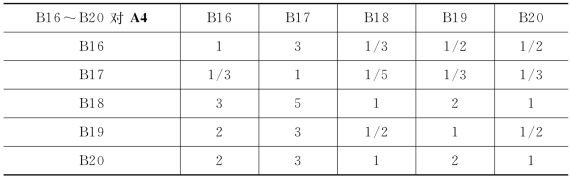
WA4=(0.133,0.066,0.333,0.185,0.283)T
表3-9 B21~B27对A5的判断矩阵

续表
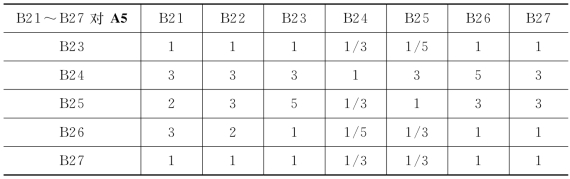
WA5=(0.081,0.079,0.081,0.329,0.231,0.114,0.085)T
表3-10 B28~B32对A6的判断矩阵
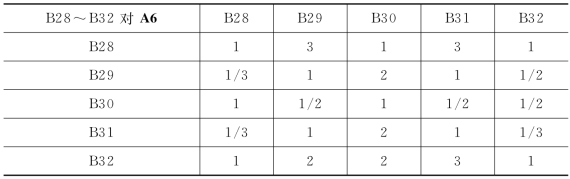
WA6=(0.290,0.148,0.135,0.138,0.288)T
表3-11 B33~B36对A7的判断矩阵
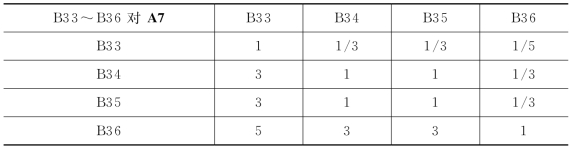
W A7=(0.079,0.201,0.201,0.519)T
表3-12 B37~B40对A8的判断矩阵

续表

WA8=(0.191,0.466,0.172,0.172)T
3.层次单排序及一致性检验
层次单排序:权向量W的元素为同一层次因素相对于上一层次因素某因素的重要性排序权值,这一排序过程称为层次单排序;层次单排序能否被确认,需要进行一致性检验。所谓一致性检验是指利用一致性指标和一致性比率小于0.1及随机一致性指标的数值表,对判断矩阵进行检验的过程。
一致性指标![]() (λ为最大特征向量,n为判断矩阵维数),其中CI越接近于0,矩阵越有满意的一致性。
(λ为最大特征向量,n为判断矩阵维数),其中CI越接近于0,矩阵越有满意的一致性。
根据本章第一节的论述,一致性比率![]() 为随机一致性指标,具体指标值见附录A),若CR的值小于0.1表明判断矩阵的不一致性在容许范围内,因此可以用判断矩阵的特征向量作为权重向量,若一致性检验未通过则需要重新构建判断矩阵,直到通过检验。
为随机一致性指标,具体指标值见附录A),若CR的值小于0.1表明判断矩阵的不一致性在容许范围内,因此可以用判断矩阵的特征向量作为权重向量,若一致性检验未通过则需要重新构建判断矩阵,直到通过检验。
对以上9个判断矩阵进行一致性检验,发现每个矩阵的CR值均小于0.1,9个判断矩阵均通过一致性检验,因此可以用判断矩阵的特征向量作为权重向量以衡量每个方案层指标对现代化体系总权重的贡献率,检验结果如表3-13所示。
表3-13 一致性检验

续表
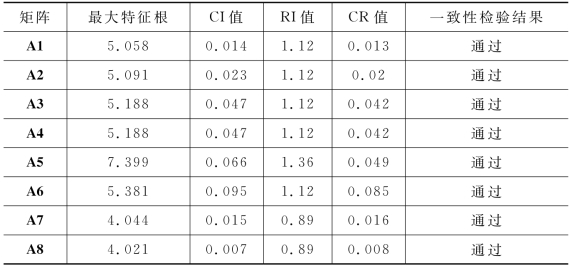
9个矩阵的权向量分别为WZ、WA1、WA2、WA3、WA4、WA5、WA6、WA7、WA8,具体权重值见前文。
4.层次总排序
根据判断矩阵计算出的权重向量,可以求出最低层对最高层的权重,即B1=0.226×0.364=0.082,B2=0.226×0.108=0.024,…,依次可以计算出B3~B40的权重,权重值见表3-1。
