全国及各省份现代化经济体系的综合评价
1.KMO和Bartlett球形检验
为了检验收敛效度和区别效度,首先要确定样本数据是否适合做因子分析,需要对各个变量对应的各项样本数据进行Kaiser-Meyer-Olkin(KMO)和Bartlett球形检验。
一般来说,KMO值小于0.5时将认为数据没能符合做因子分析的条件;处于0.5~0.6则表示数据勉强符合做因子分析的条件;处于0.6~0.7时认为数据不太符合做因子分析的条件;处于0.7~0.8时认为数据符合做因子分析的条件;处于0.8~0.9时就认为数据很符合做因子分析的条件;大于0.9表示数据非常符合做因子分析的条件。Bartlett球形检验统计量的原假设变量之间的相关矩阵为单位矩阵,Sig的值小,即认为各变量之间存在显著的相关性。
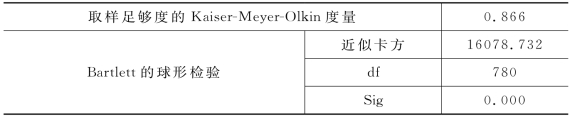
根据表3-1中的指标体系以及2010—2019年全国及各省份数据进行KMO和Bartlett球形检验,由表4-1可见,KMO=0.866且Sig=0.000<0.01,适合做因子分析。
表4-1 KMO和Bartlett球形检验
2.构建成分矩阵提取主成分
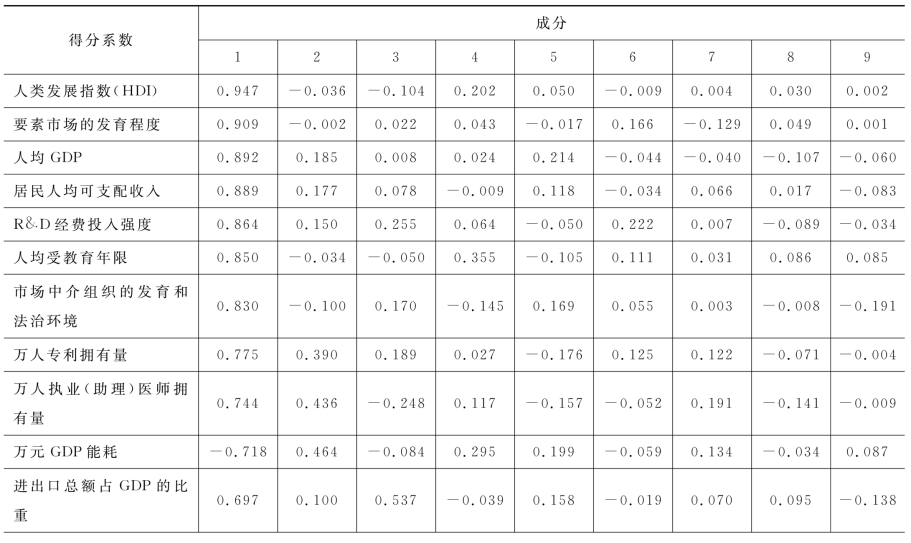
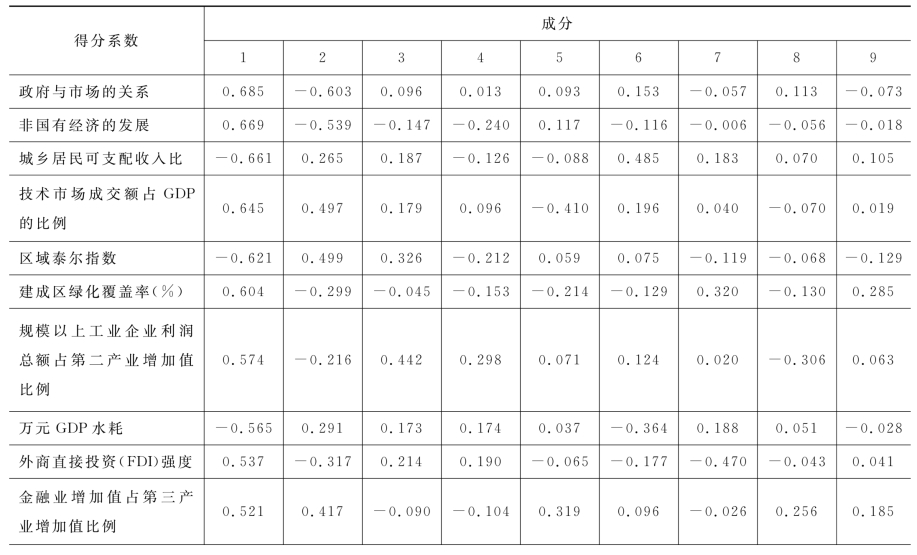
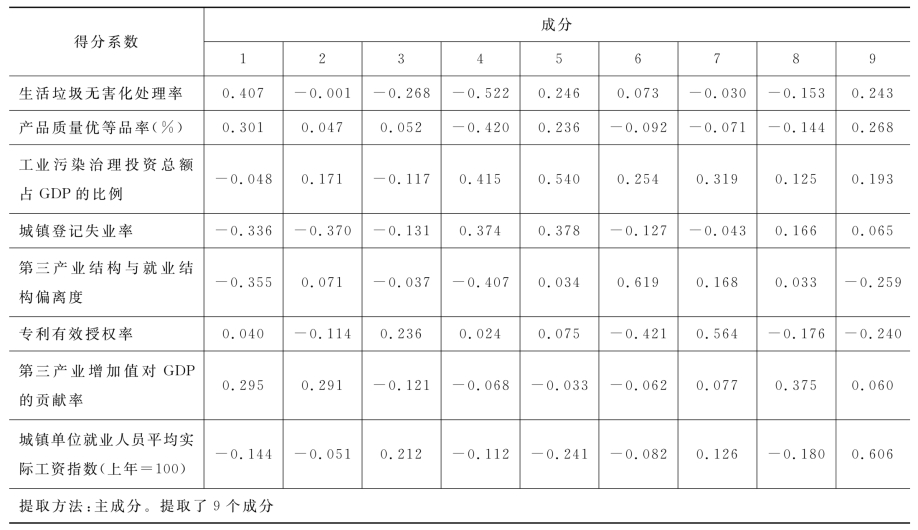
成分矩阵如表4-2所示。
表4-2 成分矩阵
续表
续表
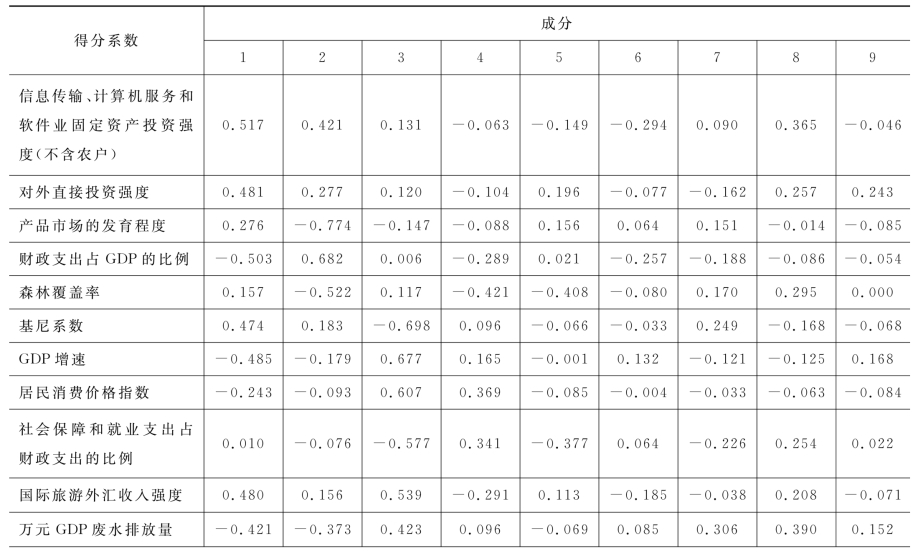
续表
3.解释的总方差
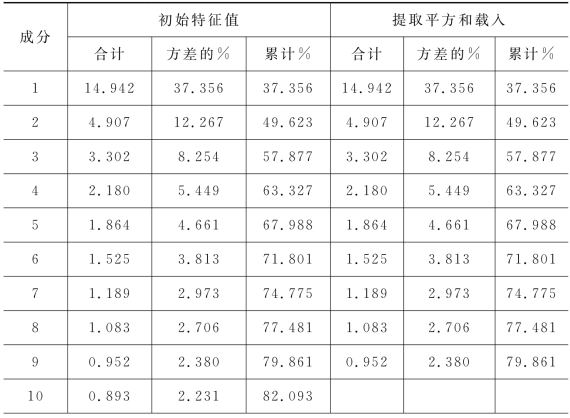
当存在多个变量时,需要考察其中的主要变量对结果的解释程度。解释方差是单个变量与总方差的方差比,解释方差表既是公因子对原有变量的解释程度,也是计算综合得分时对应公因子的权重。
通过对40个变量方差及解释方差的计算,并按其方差的初始特征值从高到低排列,表4-3共提取了8个公因子解释总的40个变量(表格省略25个变量),统计发现,8个公因子对变量的解释度达到了77.481%,9个公因子对变量的解释度达到了79.861%,差距已经不大,故提取方差初始特征值大于1的8个公因子,已经能够比较好地解释原有变量所包含的信息。因此,为了计算的方便,后续分析均只取前8个公因子(各指标公因子得分情况及公因子1、2、3的成分图见附录C、附录D)。
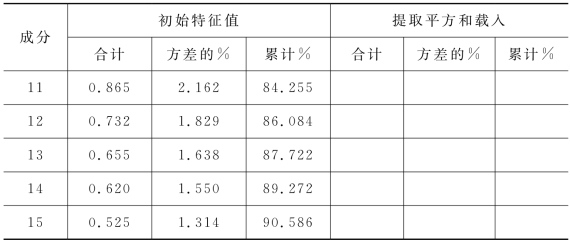
表4-3 解释方差表
续表
4.根据因子得分计算综合得分
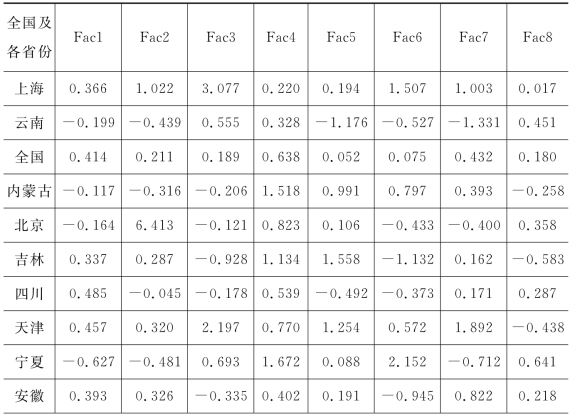
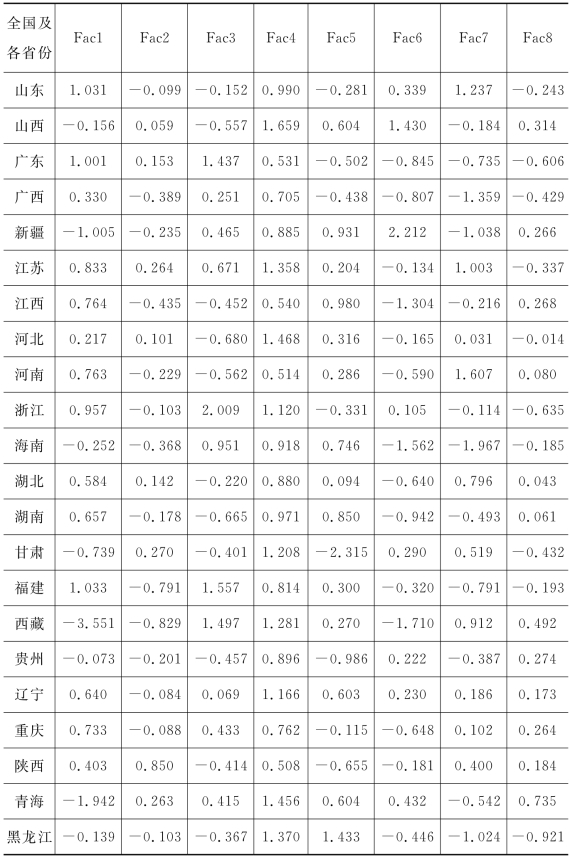
根据全国及各省份2010—2019年的各项指标数据,可以测算得到全国及各省份8个主要因子的得分(全国及各省份各年主要因子得分见附录E),如表4-4所示。
表4-4 全国及各省份8个主要因子得分
续表
因此,根据因子综合得分公式可以得到各自综合得分:
![]()
全国及各省份现代化经济体系的得分和排名情况如表4-5所示(表4-5综合得分为2010—2019年全国及各省份因子综合得分加权平均分归一化处理后的分值),可以从两个维度来看2010—2019年全国及各省份综合得分情况。
表4-5 2010—2019年全国及各省份综合得分排名
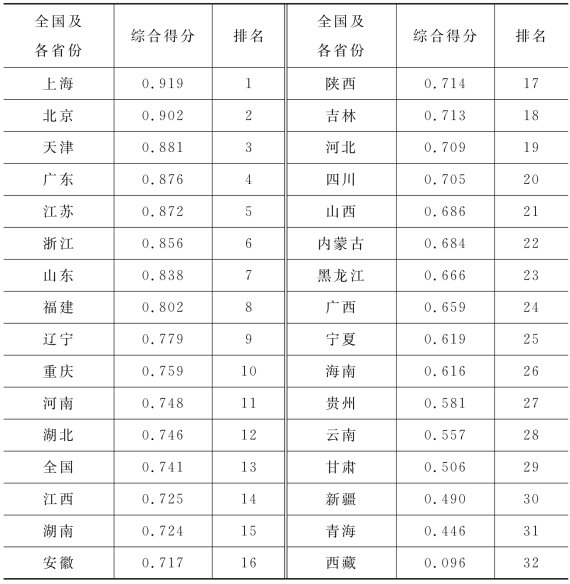
(1)从现代化经济体系的发展水平维度来看,上海、北京、天津、广东、江苏、浙江、山东和福建的现代化经济体系得分均大于0.8,处于高现代化经济体系发展水平;辽宁、重庆、河南、湖北、全国、江西、湖南、安徽、陕西、吉林、河北和四川的现代化经济体系得分介于0.7与0.8之间,处于中等现代化经济体系发展水平;而山西、内蒙古、黑龙江、广西、宁夏、海南、贵州、云南、甘肃、新疆、青海和西藏的现代化经济体系得分均小于0.7,处于低现代化经济体系发展水平。目前来看,高现代化经济体系发展水平的省份只有9个,不到总体的30%;而中低等现代化经济体系发展水平的省份有22个,占比70.97%。数据表明,中国目前的现代化经济体系总体上处于中等发展水平,但省份间的差距仍很大,现代化经济体系具有空间地域不平衡的特点,主要受到社会经济不平衡和不充分发展的制约。
(2)从全国线看的现代化经济体系发展水平差距由表4-6可以看出,全国的现代化经济体系得分为0.741,排在第13位,处于中等现代化经济体系发展水平,高于全国线的省份有12个,分别是上海、北京、天津、广东、江苏、浙江、山东、福建、辽宁、重庆、河南及湖北;而低于全国线的省份则达19个,分别是江西、湖南、安徽、陕西、吉林、河北、四川、山西、内蒙古、黑龙江、广西、宁夏、海南、贵州、云南、甘肃、新疆、青海和西藏;很多省份没有达到全国线的发展水平。排名前三位的分别是上海、北京和天津,其现代化经济体系得分均在0.9左右,属于极高的现代化经济体系发展水平;排名末尾三位的是新疆、青海和西藏,平均现代化经济体系得分仅有0.344,属于极低的现代化经济体系发展水平;排名最高的上海和最低的西藏,现代化经济体系得分差值为0.823,差距较悬殊。总的来看,东部及沿海地区与西部内陆的差距较大,西南和西北地区是我国全面建设现代化经济体系的薄弱环节,要提升全国的现代化经济体系水平,则依托区域协调发展战略和“一带一路”建设布局啃下西部这块“硬骨头”是重中之重。
