1.3.6 基于发明原理使用频次的多冲突(矛盾)问题求解
1.3.6.1 冲突(矛盾)矩阵中发明原理使用频次统计
TRIZ理论的冲突(矛盾)矩阵具体方法就是将特殊问题转换成TRIZ一般问题,通过工程参数的矛盾冲突,应用其带有普遍性的发明原理和工具寻求标准解法,在此基础上演绎形成初始问题的创新方案。运用TRIZ理论的矛盾矩阵进行实际工程创新设计的分析过程中,首先明确工程问题的设计主题范围,并收集技术发展、市场调查等相关资料,将实际工程问题进行分析与定义;其次如果存在技术矛盾,根据工程问题的技术特性需求进行问题分析与描述,将实际问题中改善及恶化的参数标准化为TRIZ的39项工程参数,在TRIZ的矛盾矩阵中查找确定的通用工程参数,找出改善参数和恶化参数所确定的推荐可用的发明原理形成冲突(矛盾)矩阵。
分析整个冲突矩阵可以发现一些发明原理具有极高的出现频次,这就意味着使用该发明原理有较大的可能性解决较多的具体冲突问题。国际著名TRIZ研究学者Mann提出,很多时候不必分析具体的冲突,而是尝试直接应用矩阵中高频率出现的发明原理,也是解决问题的有效途径之一。冲突矩阵中各个发明原理的使用频次统计分析结果如表1-3所示。
表1-3 冲突(矛盾)矩阵中发明原理使用频次统计结果
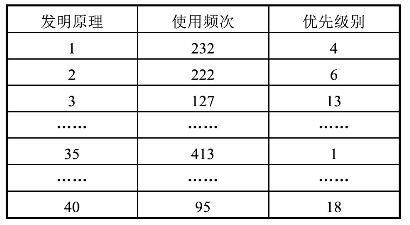
资料来源:作者根据相关资料整理。
从冲突矩阵中发明原理使用频次的统计结果(表1-3)可以看出,在冲突(矛盾)矩阵中使用频次最高的分别是35号发明原理(使用413次)、1号发明原理(使用232次)。美国科技人员在引入TRIZ理论基础上,对1500万件专利加以分析、研究、总结,发现40条发明原理中最常用的是矩阵中出现频次最高的。在此基础上,从不同视角出发,对矩阵中的发明原理及其出现频次进行分析研究,具有实际意义。
1.3.6.2 多冲突(矛盾)问题快速求解方法(https://www.daowen.com)
对于多冲突问题的解决,传统的求解思路是首先进行解耦分析,将系统重新划分为若干子系统,再转换为互不相关的若干子问题,然后分别处理每一个子问题。但是,解耦分析对于大多数工程师而言是比较复杂的设计过程,面对企业的快速设计任务显然不合适。冲突矩阵的统计分析方法为多冲突问题的快速创新求解奠定了理论基础。当实际问题存在多对冲突,尤其是耦合冲突时,解耦过程烦琐、困难,这时对于矩阵推荐的所有发明原理及其出现频次信息进行再次利用,就有可能化繁为简,快速检索得到可行的解决方案。
1.3.6.3 多冲突(矛盾)问题求解
对于同时存在的若干对冲突,如果每一对冲突都推荐某一发明原理,则意味着该发明原理可能是解决所有冲突的办法。因此,对于多对冲突推荐的发明原理及其频次进行统计分析,发现高频次发明原理意味着其覆盖冲突个数较多,其创新效果通常是显著的。针对这种情况,提出基于统计分析的方法,帮助设计者快速检索到可使用的TRIZ发明原理。
(1)根据工程问题的技术特性需求,在TRIZ的矛盾矩阵中找出所有可能的工程参数。
(2)参数之间两两排列、组合,每一个参数既作为改善的参数,又作为恶化的参数(必要时,也可选择每一个既是期望改善的参数,又是避免恶化的参数,即该参数出现设计上的物理冲突)。
(3)统计、检索所有冲突对应的发明原理,其中出现频次最高的,即认为是最有可能成功解决问题的发明原理。
(4)按照发明原理出现频次逐个或者组合应用发明原理,尝试解决多冲突问题。整个过程不需要分析多冲突问题是否存在耦合或进行复杂的解耦分析,仅需要进行简单的统计分析。该方法能快速得到具有较强可行性的、合适的、能够解决问题的发明原理,可大幅度减少多冲突问题的解耦分析难度,设计不再受制于如何优选多冲突问题的工程参数。
相比于传统多冲突问题的求解方法,该方法具有简单明了的显著特点,对于创新设计工作将发挥积极作用。快速设计流程分析和多冲突问题的快速求解关键在于能够根据给定的若干设计参数,进行排列组合,列出所有可能的冲突参数(为了实现这一目标编写算法关键代码见附录6)。
