多目标决策问题的关键要素
2026年01月15日
一、多目标决策问题的关键要素
一般的,多目标决策问题主要涉及如下5个关键要素:
(1)决策变量x=(x1,x2,…,xn)T;
(2)目标函数F(x)=[f1(x),f2(x),…,fn(x)];
(3)可行集(约束条件)
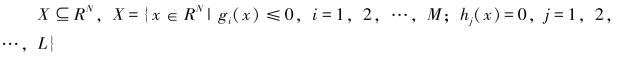 (https://www.daowen.com)
(https://www.daowen.com)
(4)对于决策者的偏好程度,在目标集F(X)={f(x)|x∈X}上存在偏好关系≺以反应决策者的偏好。
(5)解的定义,根据决策者的偏好关系≺下定义F(X)在可行域上的最优解。
与传统的单目标数学规划问题不同的是,多目标决策问题中,通常不存在使得所有目标函数同时达到优化后的最优解。换句话说,可行集x只是某一些目标函数的最优解,并不是其余目标函数的最优解。因此,在多目标决策问题中绝对最优解通常是不存在的,此时需要考虑另外一种解的概念——非劣解(帕累托有效解)。非劣解是指:在解集中,如果可行解x是非劣解,那么不存在另外的可行解x'使得x'的各个函数目标值fk(x'),k=1,2,…,n都不劣于可行解x的各个目标函数值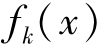 ,k=1,2,…,n,同时还满足至少有一些k0,fk0(x')都要优于fk0(x)。然而,在解集中一般存在很多的有效解,使得多目标决策的一个本质问题就是如何根据系统和决策者的主管判断价值对非劣解进行优选和比较。决策者的主观价值判断表现为他认为某些可行解x比x'更好(或者说f(x)比f(x')更好),也就是在X(或f(x))上定义了一个二元偏好关系。
,k=1,2,…,n,同时还满足至少有一些k0,fk0(x')都要优于fk0(x)。然而,在解集中一般存在很多的有效解,使得多目标决策的一个本质问题就是如何根据系统和决策者的主管判断价值对非劣解进行优选和比较。决策者的主观价值判断表现为他认为某些可行解x比x'更好(或者说f(x)比f(x')更好),也就是在X(或f(x))上定义了一个二元偏好关系。
一般而言,决策者根据某种决策规则和偏好关系在非劣解之间进行有效权衡,从而找到最终的满意解,但是不同的决策者在非劣解解集中选择的满意解一般是不同的。
