模型求解及结果分析
(1)选址方案比较
该区被岷江穿境而过,是度假、探险、休养的胜地,旅游资源丰富。根据全县污水总量,选址原则和县域工业发展的具体情况,污水处理厂设计的处理能力在2万到5万平方米/天之间。考虑到建设规模和周边地区,工厂的规划面积约为10,000-50,000立方米。通过相关人员在规划过程中进行的初步调查和征求有关方面的意见,根据建设污水处理厂的原则和要求,选定了3个相对令人满意的选址方案。详情如下:
方案一:污水处理厂可建在坡度40度的山坡上。而工厂土地需要平整,因此土方工程的资金成本被评估为19万美元。
方案二:污水处理厂可以建在一个带防洪墙的河岸上,用于解决洪水问题。由于防洪墙的钢筋混凝土结构,总共需要4800立方米的钢筋混凝土。计算钢筋混凝土综合成本为63.49美元/立方米,所需投资304.76万美元。
方案三:污水处理厂可建在没有防洪墙的河岸上。在这种情况下,加工设备需要调整。值得注意的是,该方案采用了ICEAS工艺(改进的SBR技术)。采用这个过程可以完全避免曝气设备的防洪缺陷。在洪水发生前,我们只需移动普通活动元件,而不用担心污水处理厂的关键设备。
上述方案中污水处理厂的全部资本性支出情况如表3-9所示。此外,所有方案的再生水回用率为30%,单位回收水经济效益为0.19美元/立方米。
表3-9 所有方案的成本计划
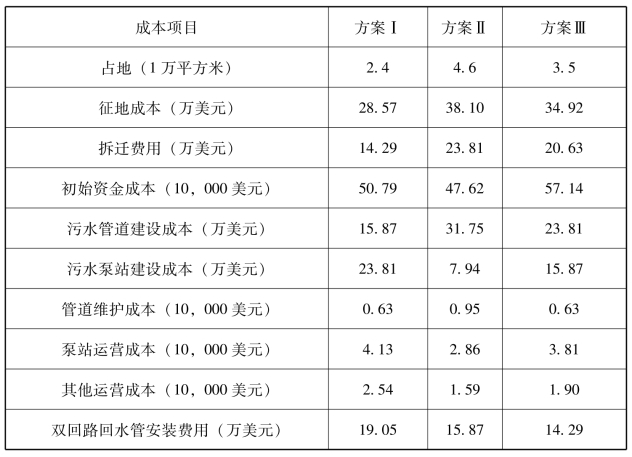
(2)排放标准及工艺技术
为便于计算,本文假定污水源的进水浓度在该地区是一致的。由于生活污水占县城污水的比例很大,工业废水属于一般工业污水,所以COD和NH3-N是主要污染物。进入该地区处理厂的污水进水质量确定为:
![]()
根据河流系统分布和污水处理厂,处理后的水最终流入岷江及其支流。按照GB18918-2002“城市污水处理厂污染物排放标准”的B标准,处理厂出水水质要求如下:
![]()
建议的进水和出水水质以及处理厂的污染物去除率见表3-10。
表3-10 污水处理厂设计的进水和出水水质和污染物去除率
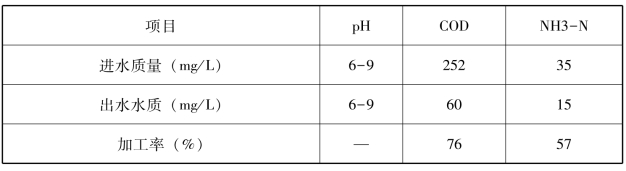
在综合技术经济约束条件下选择污水处理工艺,出水水质的要求,结合成都地区的实际情况,本研究选择了氧化沟,ICEAS和A/A/O法作为替代方案(见图3-13)。
表3-11列出了氧化沟,ICEAS和A/A/O的结构,并且显示出一些结构是一致的,而一些结构是不同的。表3-12列出了不同结构所需的设备。
表3-11 三种污水处理过程结构之间的比较
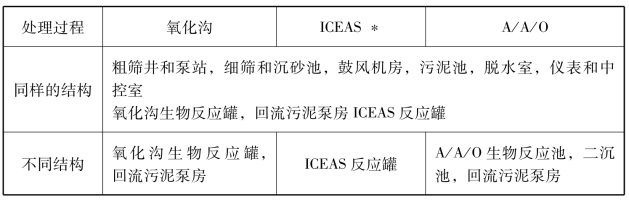
*ICEAS:间歇循环扩展曝气系统
表3-12 三种污水处理设备的比较
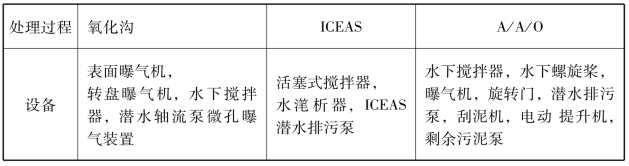
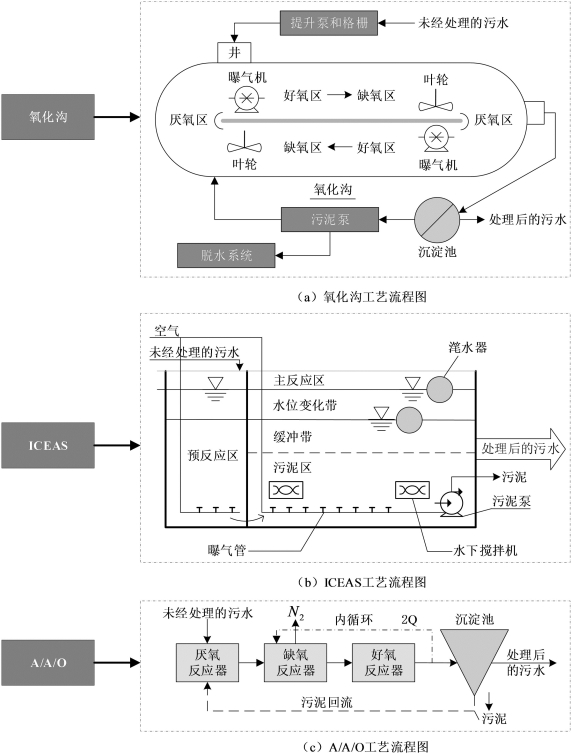
图3-13 三种污水处理工艺流程图(https://www.daowen.com)
总而言之,相同规模的污水处理厂的设备成本差异主要在于生物处理单元结构的各种设备。因此,我们在建立模型时将设备成本整合在一起。
(3)模型求解及分析
污水处理厂的总成本包括初始投资成本和本研究的运营成本。另外,实际计算中的初始投资成本和运营成本的具体形式是不同的。在这种情况下,污水处理厂的初始投资成本包括表3-13中提到的成本以及不同技术方面的不同工艺投资成本。为了便于计算,三种技术的初始投资成本模型是从其他文献中借用的,并在这种情况下使用,如表3-13所示。
表3-13 三种污水处理过程的初始投资成本

运营成本主要集中在管道维护、能耗、设备维修等方面。除表3-14中列出的运营成本外,还包括来自不同流程的污水处理成本。在本文中所提出的模型通过启发式算法-遗传算法(GA)来求解,因为直接求解具有挑战性。图3-14说明了应用遗传算法的基本过程。
表3-14 三种污水处理过程的运行成本

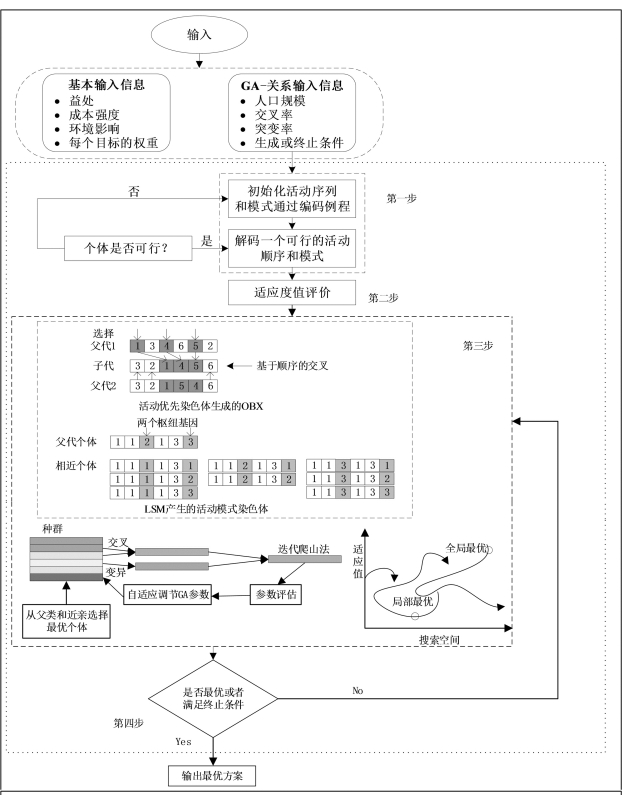
图3-14 遗传算法的基本步骤
该问题中遗传算法的参数如下:交叉率为0.2,变异率为0.4,种群规模为25,最大代数为500。
依次将权重分配给4个目标函数:
![]()
经过计算,这种情况下多目标模型的最优结果是:
![]()
因此,在最优解下,最小费用为4.19×106美元;最大经济效益2.17×104美元;COD和氨氮的去除率分别约为85.1%和93.2%。因为x1=x2=0,这意味着方案Ⅰ和方案Ⅱ没有被考虑,任何分配给设计容量和模型中COD和氨氮去除率的任意值都是没有意义的。
以上结果表明,在规划面积1万~5万平方米的范围内,为实现达到2万~5万立方米/天的设计能力,满足最低投资成本要求的目标,应选择方案三。方案一采用建设高原污水处理厂的方法,增加土方投入和年度运营成本。通过分析,本文认为方案一在经济上不可行。在方案二中,污水处理厂周围是防洪墙,造成一系列问题,如投资大,景观影响大。方案三采用规定安装潜水排污泵和射流曝气装置,规划控制室,在污水处理厂房内安装局部高程的电气化改造配电设备。虽然投资增加到一定程度,但整体增幅并不算太大。因此,方案三在技术上可行,经济上合理。
在技术方面,虽然方案三只采用了ICEAS工艺,但依然可以有效处理污水中的污染物并降低其含量,满足污染物排放总量控制的要求。这是由于该地区的主要污水由生活污水组成,生物降解性较好;同时,ICEAS工艺是次生化处理,使COD和氨氮去除率分别达到85.1%和93.2%的较高水平。相反,即使方案一和方案二中的可选过程可以达到前面讨论的预期效果,由于其更高的建设和运行成本,它们在经济上受到限制。
从环境保护的角度来看,方案三也是基于现实的考虑。处理后的污水COD和氨氮浓度分别计算为35.63mg/L和2.39mg/L,完全符合GB18918-2002“城市污水处理厂污染物排放标准”一级标准。此外,该方案定位在没有围拢它的防洪墙的河岸。只需按照正常要求铺设结构基础,不会对周围环境(包括水体,地下水,耕地,森林,水产品,景观,风景名胜,自然保护区等)造成不可逆转的损害。此外,它既不位于城市或住宅区的上风区,也不位于城市水资源的上游。因此,处理厂也不会影响居民的正常生活。
根据决策者对每个目标的重视程度,对每个目标函数赋予不同的权重。表3-15说明了条件和最优决策结果的每个目标函数的值。
表3-15 不同重量条件下的最优决策结果
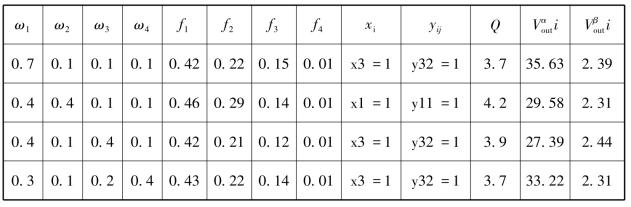
建设成本是建设处理厂时考虑的主要因素;因此,它通常被赋予更大的权重值。根据对再生水效益和污染物排放量的重视程度调整重量。从表3-15可以看出,成本权重调整和再生水效益对决策结果影响显著,而污染物处理效率或污染物排放权重变化不会对决策结果产生实质性影响。
根据一个地区的实际情况和发展规划,我们可以调整参数,如修改污水量和再生水回用率。通过这种调整,我们可以建立一个新的情况,建立不同的多目标决策模型来建设一个处理厂,并通过计算获得各种相应的结果。由于这种情况下的一些参数是基于同等水平的其他城镇的相关数据计算得出的,因此相关数据可能不会与相应的数据精确匹配,某种指标的调整不会对决策结果产生重大影响,这与实际情况相矛盾。所以决策者应充分了解其实际应用的具体特点,因为数据的准确性决定了模型的准确性。然而,在实际应用中,研究人员可以在一定程度上调整此模型,并将此灵活性与实际情况结合使用,从而更好地反映给定问题域的实际情况。
