多目标决策问题的模型结构
（一）模型结构
一般的，多目标决策问题可以构建成如下模型：
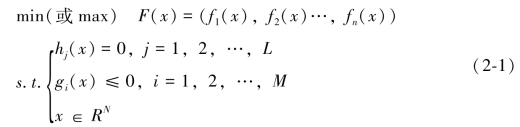
即可行域为X⊆RN，X={x∈RN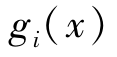
≤0，i=1，2，…，M；
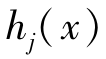=0，j=1，2，…，L}
（二）多目标优化的解集
对于多目标优化问题的解集，通常不存在x*∈X，使得目标函数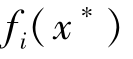
∀i∈［1，n］同时达到最优值，因此，在多目标优化问题中，其解集可以根据偏好关系定义绝对最优解、有效解和弱有效解。
在描述多目标优化问题的解集之前，我们来定义多目标优化里面的相等、严格小于、小于、小于且不等于（支配）的含义。假设RN是所有N维实数向量空间，其中有y=（y1，y2，…，yN）T，z=（z1，z2，…，zN）T，则：
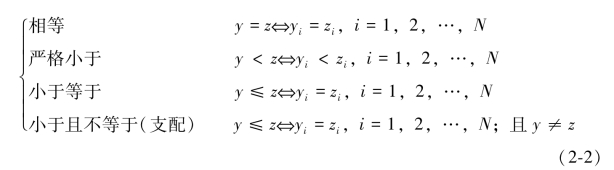
下面我们按照公式（2-2）的记号来给出帕累托最优解的相关概念：
（三）解集的相关概念
帕累托支配：对于∀x1，x2∈RN，当k取遍所有的值（k=1，2，…，n）都有fk（x1）≤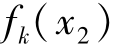
，则称x1支配x2。
绝对最优解：设x*∈D，如果对于x∈D，都有f（x*）≤f（x），也就是说当k取遍所有的值（k=1，2，…，n）都有fk（x*）≤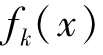
，我们称x*是多目标决策问题的绝对最优解。
有效解：设x*∈D，如果不存在x∈D，使得f（x）≤f（x*），也即满足条件fk（x）≤fk（x*），且∃i∈［1，K］，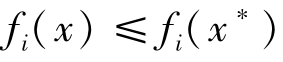
，则我们称x*是多目标决策问题的有效解。有效解也称为帕累托最优解，其含义是当x*是帕累托最优解时，则在解集中找不到这样的可行解x∈D，满足决策者偏好情况下使得f（x）的每个目标值都不比f（x*）的目标值差，并且f（x）至少有一个目标比f（x*）的相应目标值好，就是说x*是最好的，不能再进行改进。
弱有效解：设x*∈D，如果不存在x∈D，使得f（x）＜f（x*），也即满足条件fk（x）≤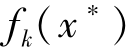
，且∀k∈［1，K］，则我们称x*是多目标决策问题的弱有效解。弱有效解的含义是如果x*是多目标问题的弱有效解，则找不到另外的可行解x∈D使得f（x）的每个目标值都比f（x*）的目标值严格（＜）的好。
帕累托最优解集：给定多目标决策问题的有效解（帕累托最优解）所构成的解集，我们称这个解集为帕累托最优解集。需要注意的是帕累托最优解集中的解是相互非支配的，即两两不是非支配关系。
帕累托最优前沿：帕累托最优集中每个解对应的目标值所组成的集合称为帕累托最优前沿，可以用图2-1来表示。
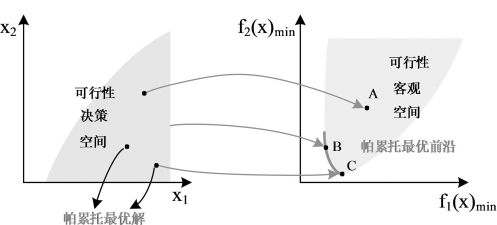
图2-1 帕累托最优前沿