多目标优化的最优性条件
前面我们已经介绍了多目标决策的一些基本概念,对于多目标决策问题求解而言,一般是将多目标问题转换为单目标问题。然而对于单目标问题,其解的最优性条件是由库恩和塔克(Kuhn &Tucker)在1951年推导并证明,我们称此最优性条件为Kuhn-Tucker条件,该条件后面逐渐成为目标规划中众多算法的基础。本节将从单目标决策问题的Kuhn-Tucker条件从发,介绍多目标决策问题的Kuhn-Tucker条件。
(一)单目标决策问题的Kuhn-Tucker条件
我们知道,单目标决策问题的一般形式表达如下:
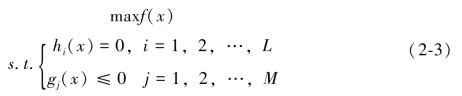
其中,称x为欧式空间中的n维决策变量,也即是由n个决策变量组成的决策向量,有x=(x1,x2,…,xn)。为了便于理解和计算,我们规定f(x),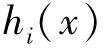 ,
,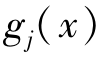 (i=1,2,…,L;j=1,2,…,M)具有一阶连续偏导数。
(i=1,2,…,L;j=1,2,…,M)具有一阶连续偏导数。
在给出Kuhn-Tucker条件之前,我们先介绍几个关键概念,以便于厘清该条件的具体定义和算法流程。
正则点的定义如下:假设x*是满足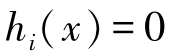 和
和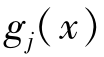 ≤0的点,令m是使得
≤0的点,令m是使得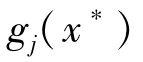 =0的所有下标j的集合。如果梯度向量
=0的所有下标j的集合。如果梯度向量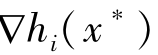 ,
,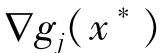 (i=1,2,…,L,j∈m)是线性无关的,我们称x*为式(2-3)约束条件中的一个正则点。
(i=1,2,…,L,j∈m)是线性无关的,我们称x*为式(2-3)约束条件中的一个正则点。
其中梯度向量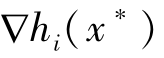 ,
,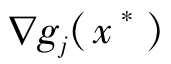 (i=1,2,…,L,j∈m)定义为:
(i=1,2,…,L,j∈m)定义为:
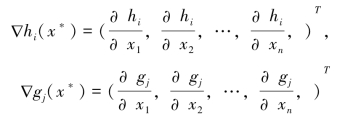
于是,我们将式(2.3)的Kuhn-Tucker最优性条件阐述如下:
设f(x),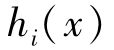 ,
,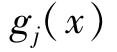 在欧式空间中的某一开集上一阶连续可微,如果x*是式(2-3)约束条件中的一个正则点,则存在Lagrange乘子集
在欧式空间中的某一开集上一阶连续可微,如果x*是式(2-3)约束条件中的一个正则点,则存在Lagrange乘子集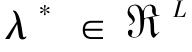 和μ*∈ℜM,并且有μ*≥0,使得如下条件成立:
和μ*∈ℜM,并且有μ*≥0,使得如下条件成立:
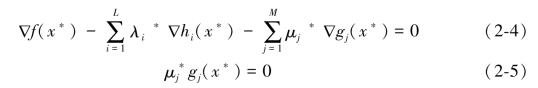 (https://www.daowen.com)
(https://www.daowen.com)
我们取x*为式(2-3)中满足约束条件的正则点,假设存在Lagrange乘子集λ*∈ℜL和μ*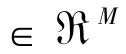 ,并且有μ*≥0,有式(2-4)和(2-5)成立。
,并且有μ*≥0,有式(2-4)和(2-5)成立。
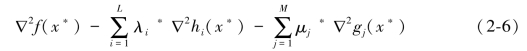
为正定矩阵,那么x*为式(2-3)中的局部最小值。
另外对于求解极小化的单目标优化问题,可以通过增加负号将其转化为求解极大值问题,进一步再利用Kuhn-Tucker条件进行求解。
(二)多目标决策问题的Kuhn-Tucker条件
本节以最大化多目标决策问题为例,其一般模型如下:
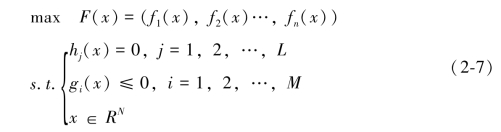
即可行域为X⊆RN,X={x∈RN|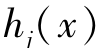 =0,j=1,2,…,L;
=0,j=1,2,…,L;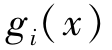 ≤0,i=1,2,…,M}。我们已经知道,式(2-7)一般没有最优解,但可以找到其非劣解。
≤0,i=1,2,…,M}。我们已经知道,式(2-7)一般没有最优解,但可以找到其非劣解。
结合前面单目标决策问题的Kuhn-Tucker条件,式(2-7)的解的非劣性条件和式(2-3)的最优性条件非常相似。在这里,我们首先给出式(2-7)的非劣解的Kuhn-Tucker必要性条件如下:
设向量x∈X,并且有x是满足式(2-7)中的正则点。同样,这里fk(x),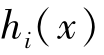 ,
,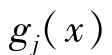 (k=1,2,…,n;i=1,2,…,L;j=1,2,…,M)满足连续可微条件,如果x是式(2-7)的非劣解,则必然存在Lagrange乘子集向量γ,λ和μ, 其 中γ=(γ1,γ2,…,γn)T,λ=(λ1,λ2,…,λL)T,μ=(μ1,μ2,…,μM)T,并且满足γk≥0,γk0≥0,k=1,2,…,n,1≤k0≤n,λi≥0,i=1,2,…,L;μj≥0,j=1,2,…,M使得
(k=1,2,…,n;i=1,2,…,L;j=1,2,…,M)满足连续可微条件,如果x是式(2-7)的非劣解,则必然存在Lagrange乘子集向量γ,λ和μ, 其 中γ=(γ1,γ2,…,γn)T,λ=(λ1,λ2,…,λL)T,μ=(μ1,μ2,…,μM)T,并且满足γk≥0,γk0≥0,k=1,2,…,n,1≤k0≤n,λi≥0,i=1,2,…,L;μj≥0,j=1,2,…,M使得
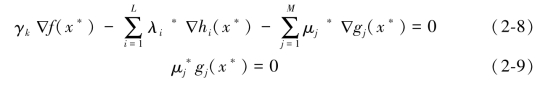
本节将不在讨论一般多目标决策问题非劣解的充分条件,仅给出凸规划情形下的结论:若目标函数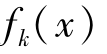 (k=1,2,…,n)均是凸函数,并且所有的γk≥0(k=1,2,…,n),其可行域X是凸的,则式(2-8)和(2-9)也是x为非劣解的充分条件。
(k=1,2,…,n)均是凸函数,并且所有的γk≥0(k=1,2,…,n),其可行域X是凸的,则式(2-8)和(2-9)也是x为非劣解的充分条件。
