三、蚁群算法

三、蚁群算法

（一）算法起源

蚁群算法（Ant Colony Optimization）是Dorigo于1992年在其博士论文中提出的一种寻找最优路径的智能优化算法，属于概率型算法，它是受自然界中客观存在的蚁群在寻找食物源过程中的行动路径和信息传递的启发而发现的。蚁群算法被提出时主要用于解决旅行商中路径最优问题，后逐渐推广至大规模离散系统中存在的最优问题。该算法本身具有比较强的鲁棒性，且其优良的分布式计算机制促使蚁群算法便于和其他仿生智能算法相结合，拓宽了其应用范围，现在常用来解决大规模组合优化问题、选址问题、凸优化问题、机器学习和数据挖掘方面的寻优问题。

（二）算法思路

蚂蚁寻找食物源过程中的行动路径极其简单，其行为数量在10种以内。但是，蚂蚁寻找食物是一种群体型行为，成千上万只蚂蚁能够拥有巨大的智慧，这需要它们在行动路径中进行信息互动-信息素传递。这种信息素能够标识蚂蚁行走的路径。在寻找食物源的过程中，蚂蚁根据信息素的浓度选择前进的方向，并能够到达食物所在的地方。

在寻找食物源过程中，最开始的路径中没有信息素，因此蚂蚁行走的路径是随机的。在随机过程中会不断释放信息素，标识自己的行走路径。随着时间的推移，开始寻找食物源的蚂蚁寻找到了食物，此时可能存在很多条从洞穴到食物源的路径。然而蚂蚁的行动轨迹的随机分布的，因此在单位时间内，短路径上的蚂蚁数量比长路径上的蚂蚁数量要多，那么短路径上的信息素浓度也就相对越高。这为后面的蚂蚁们提供了强有力的方向指引，会不断有蚂蚁聚集到最短的路径上去。在长路径上的信息素会随着时间的推移而逐渐挥发。

蚁群算法整体背景可以概括如下：

（1）高度结构化的组织-尽管蚂蚁的个体觅食行为极其简单，但其群体觅食却能够组成高度结构化的社会组织，单只蚂蚁有明确的分工，且还有信息互通和传递。

（2）群集智能优化-蚁群在觅食过程中，在没有任何信息提示下能够有效找到洞穴到食物源的最短路径，同时还能绕过障碍物寻找最优。这是依靠觅食过程中蚁群间的信息传递。

（3）信息正反馈-蚁群在觅食过程中，在其行动路径上释放信息素，在其他蚂蚁选择行动路径时，会根据路径上的信息素浓度进行选择，并倾向于朝着信息素浓度高的路径上移动。

（4）自催化行为-当某条行动路径上走过的蚂蚁越来越多时，路径上留下的信息素也越多（随时间蒸发一部分），其信息素强度将增大，后来蚂蚁选择该路径的概率也越高，从而进一步增加该路径的信息素强度。

（三）算法具体流程

结合前面介绍的蚁群算法基本思路，可以将蚁群算法的具体步骤总结如下：

（1）根据最优问题设置初始化蚂蚁数量，初始信息素数量并设置为相等，分头并行搜索；

（2）每只蚂蚁在寻找食物源的行动路径上释放信息素，信息素越多，表明该路径更优，信息素越少，表明该路径越差。也即解的质量与信息素成正相关；

（3）蚂蚁路径的选择根据信息素强度大小，同时考虑两点之间的距离，采用随机的局部搜索策略。这使得距离较短的边，其上的信息素量较大，后来的蚂蚁选择该边的概率也较高；

（4）每只蚂蚁只能走觅食过程中的路线，为此设置禁忌表来控制好寻优；

（5）所有蚂蚁都搜索完一次就是对整个解空间迭代一次，而每迭代一次就对所有的解（蚂蚁）进行一次信息素更新，将产生新的解（蚂蚁），新的解（蚂蚁）将进行新一轮的并行搜索。

（6）更新信息素包括对原有信息素的挥发和寻优路径上信息素的增加。

（7）达到满足条件的迭代步数，或出现停滞现象（所有蚂蚁都选择同样的路径，解不再变化），则算法结束，以当前最优解作为问题的最优解。

（四）表达方式

我们以旅行商问题（Travelling salesman problem，TSP）的最短路径为例，来具体描述蚁群算法的实现过程。旅行商问题是指给定n个城市，一个旅行商从某一个城市出发，访问各城市一次且仅有一次后返回到原出发城市，要求寻找一条最短的旅行路径。我们把旅行商抽象为蚂蚁，并进行如下问题描述。

假设n个城市的集合表示为C={c1，c2，…，c3}，集合C中两两城市的集合表示为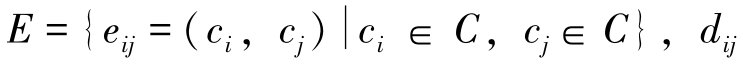表示边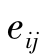的欧式距离，i，j=1，2，…，n，G=（C，E）是一个有向图，旅行商问题的目的是从G中寻找出长度最短的路径。

m代表蚂蚁数量，k表示蚂蚁编号，t表示时刻，ηij代表启发因子，用来表征蚂蚁由城市i转移到城市j的启发程度，τij表示边eij上的信息素，Δτij表示每经过一次迭代边eij上的信息素增量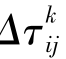，表示第k只蚂蚁在本次迭代过程中在边eij上留下的信息素量，ρ代表信息素挥发的系数（0＜ρ＜1），1-ρ表示信息素持久性系数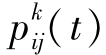，表示时刻t蚂蚁k由城市i转移到城市j的转移概率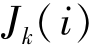，表示蚂蚁k下一步行动选择的城市集合

计算公式如下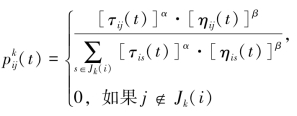：如果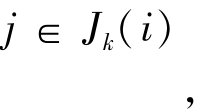

（i）城市转移概率这里α表示信息素的相对重要程度，β表示启发式因子的相对重要程度。

（ii）其中启发式因子的计算公式：

（iii）初始化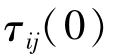=Γ，也即每条边上的信息素量均相等。当所有蚂蚁完成一次搜索后，各个行动路径上的信息素为：

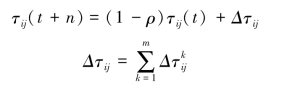
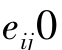若蚂蚁k在本次搜索中经过边，否则，这里Q为大于0的正常数，Lk为蚂蚁k在本次搜索过程中所走路径的总长度。

（五）算法步骤

（i）初始化参数：设置每条边的信息素量均相等，即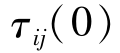=Γ，且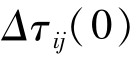=0，蚁群规模数量m，信息素重要程度α，启发因子相对重要程度β等；

（ii）将各个蚂蚁设置各定顶点，禁忌表为对应的顶点；

（iii）计算每只蚂蚁的城市转移概率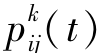，随机选择下个一顶点，更新禁忌表，再次计算转移概率，再选择顶点，再更新禁忌表，直到遍历完所有顶点1次，即成功迭代一次；

（iv）计算每只蚂蚁留在各个边的信息素增量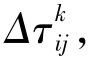重复步骤（3），直到m只蚂蚁均周游完毕，蚂蚁迭代更新；

（v）计算各边的信息素增量Δτij和信息素量；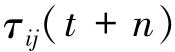

（vi）记录本次迭代的行动路径，更新当前最优路径，清空禁忌表；

（vii）判断是否达到最优解的要求，或者看是否出现停滞现象。若是，则算法结束，输出当前最优路径；否则，重复步骤（2）-（7），进行下一次迭代。

算法流程图如图2-11

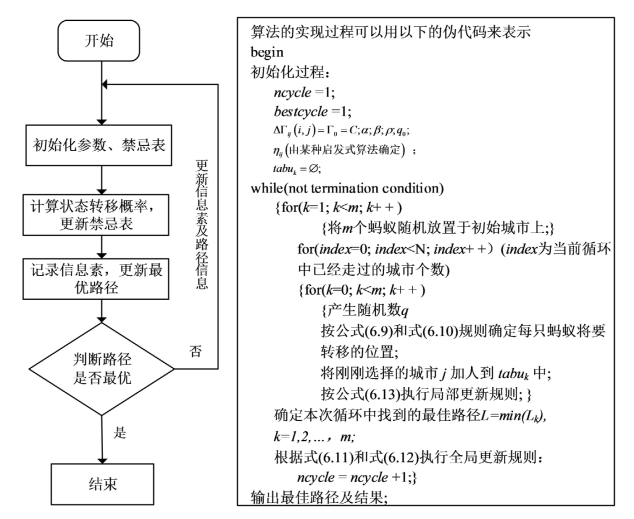
图2-11　蚁群算法流程图