协同分配权衡分析
本文将上述所建立的多目标模型应用于岷江流域，验证了该模型的可行性、有效性和实用性，并运用折中规划求解模型来权衡效率与公平，得到岷江流域8个子区域分水量、8个子区域污水可排放量分配方案。为了验证模型结果的可靠性，目标权衡分析以及公平与效率的权衡分析将在后面两个小结中讨论。
在CP模型中，k被设置1，ω1和ω2分别表示max（AUS）和min（Gini）的权重，其中（ω1+ω2=1.）。在求解模型时，可以计算每个函数的最优值和最差值，故CP模型的目标函数可以表示为：
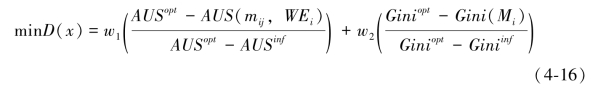
其中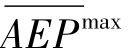
和
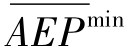分别为AEP的最优值和最差值，对其分别进行优化，并受到所开发多目标模型的约束；Gini max和Gini min分别为基尼系数的最优值和最差值，也对其分别进行优化，同时也受到所开发多目标模型的约束。
通过Eq.（15）规划求解，设置了一些典型权重，作为所有权重的一小部分，各种权重集的CP模型的分配方案结果如表4-6和图4-3所。根据基尼系数的定义（Gini，1921）可知，当基尼系数小于0.2时已绝对公平，0.2-0.3之间时较为平均，0.3-0.4之间时比较合理，0.4-0.5时差距过大，大于0.5时差距悬殊。因此，表4-6中基尼系数的结果在0.3-0.4之间是合理的，这意味着该模型能够有效地度量流域水资源和污水排放量的配置公平性。此外，表5中AUS平均值4.37×106元，给出的9种分配方案中
平均值为50700.4503亿元，这意味着水资源与排污权的协同配置能够有效促进水资源的利用效率，并能够产生对应的经济效益，进一步表明协同配置的合理性和可行性。根据表5的结果，两个目标之间的关系变得明显，因为两个目标函数值在同一方向上增加，但每个目标的相对最优值是相反的。换句话说，随着Gini系数的权重增加，AUS逐渐降低。
表4-6 不同权重集的分配方案（109m3，2019年）
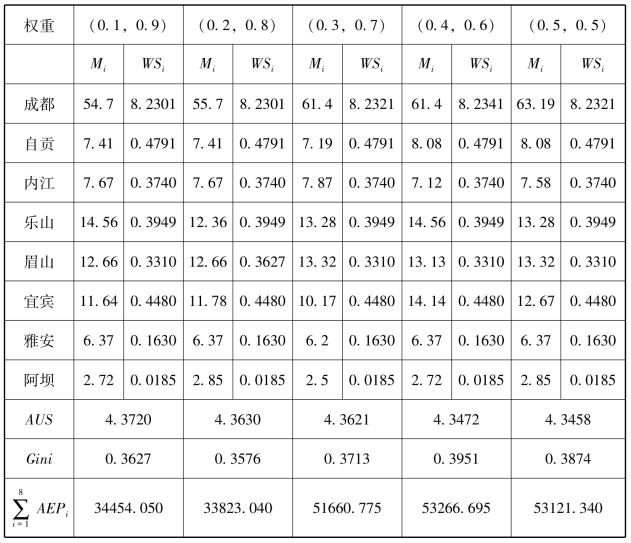
续表
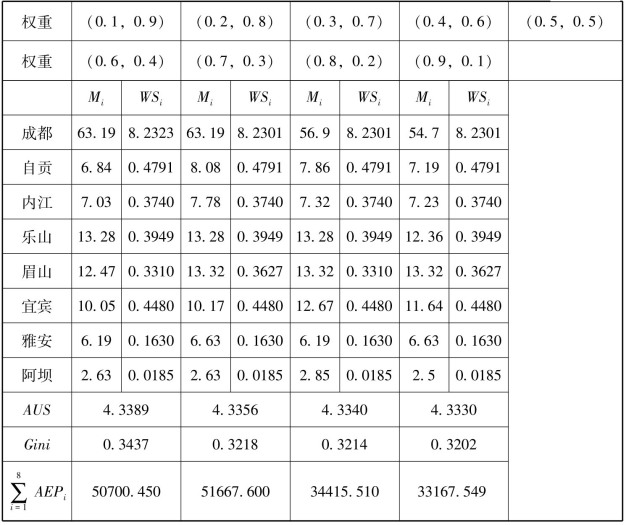
注：Mi和WSi的单位是109m3，AUS的单位是106yuan/m3，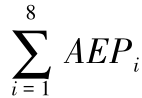
的单位是109万人民币。
根据表4-6和图4-3的结果，给出了不同权重集下各个区域的配水方案和污水排放权的分配，我们可以发现，各个区域的污水排放权分配变化并不显著，而岷江流域8个子区域的分水量被分成三个类别，第一类为成都，其分水量在54.7×109m3到63.19×109m3之间；第二类为乐山、眉山、宜宾，其分水量在10.17×109m3到14.17×109m3之间；第三类为自贡、内江、雅安、阿坝这四个子区域，其分水量在2.5×109m3到8.08×109m3之间。造成这种差异的主要原因是成都的经济总量占岷江流域总量比例最高，所需要的水也比其他7个市区更多；从2.3部分的原始数据和我们模型给出的分配方案，就已经印证了我们的结论和模型的可靠性。另外，根据图4-3，我们也可以看出8个区域在不同权重集下分水策略的敏感性，成都和宜宾都是岷江流域上经济发达的区域，它们之间的用水冲突将直接导致整个流域分水策略的用水冲突，而其他区域并没有表现出较强的敏感性。
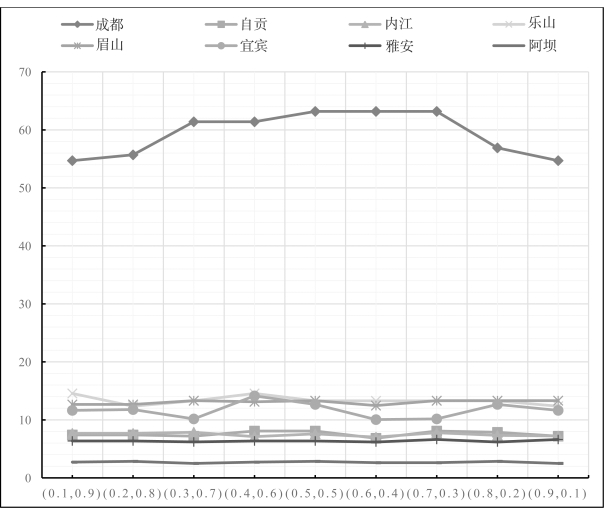
图4-3 各权重集下的分水方案
表4-6和图4-3的结果表明，本文建立的模型中水资源分配结果主要取决于流域管理当局对单方污水排放所产生的经济效益和各个区域分水公平性的偏好，同时还不能忽视流域经济发展对分水公平性的影响。
权衡冲突分析
上面给出了整个模型在岷江流域水资源与污水排放权协同配置的可靠性，流域管理者在制定具体配置方案时，需要根据流域发展需要制定不同的配置方案，从不同的角度去度量分水方案的可实施性。
表4-6和图4-4表明，当流域管理者偏向公平性时，流域总体公平性变化在0.3和0.4之间波动，Gini系数变化趋势表现为先增加后减少，最后趋于稳定状态。当公平性权重在0.1到0.4时，Gini系数逐步增加，这是由于在协同配置之间的矛盾相互作用中单方污水经济效益依然占据较大权重，使得公平性的实际占比依然较小，进而导致配置方案的公平性降低；当公平性权重在0.5到0.7时，Gini系数的值从0.39逐级递减至0.32，此时公平性在协同配置冲突中占比较大，配置方案的公平性得到上升；当公平性权重在0.8到0.9变化时，协同配置之间的冲突达到平衡，配置方案的公平性趋于稳定。由此表明协同配置方案的公平性在一定程度上取决于协同配置中流域水资源管理者对公平性与经济效益的偏好程度。另外，在不同的权重集下单方污水经济效益在4.3330×106到4.3720×106百万元之间变化，总体上呈现出逐步递减的趋势。由于在协同配置过程中单方污水经济效益与公平性之间相互制约，因此单方污水经济效益与公平性的变化总体趋势变化相反。换句话说，随着单方污水经济效益的权重增加，Gini系数将不断减小。
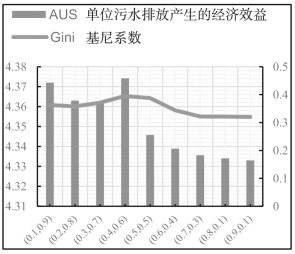
图4-4 各权重集下的基尼系数与AUS经济效益、经济效益总值
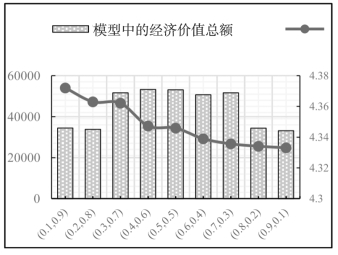
图4-5 各权重集下单位污水排放
结合表4-6和图4-5的结果，表明随着单方污水排放经济效益偏好度的增加，单方污水排放经济效益逐步递减并处于稳定状态，也就是说流域水资源管理者对经济效益的偏好在超过一定的权重时，经济效益不会随着污水排放权的分配增加而增加。那么在配置方案中，分水策略就应该依此为临界点作为水资源管理者的理想配置状态。另外，根据图4-5显示，单方污水排放经济效益目标函数的权重超过0.7时，流域总经济并没有提升反而是下降，这可能是因为经济发展产生的污水限制了流域经济发展，还可能会进一步增加污水处理的成本，同时还可能造成环境污染。
通过上述分析，配置方案的公平性能够提供平衡区域发展、减少污水排放冲突的配置策略，进一步表明公平与效率权衡的方法是可行的。
就具体经济效益而言，从岷江流域各区域发展差异来看，成都作为流域主要的经济支撑区域，其需水量和污水排放均占据较大比重，本研究给出的模型结果也表明了这一点（表4-6）。此外，本研究给出的模型还表明各个子区域根据流域管理当局对总目标函数权重的不同来制定相应的水资源分配和污水排放策略，以确保社会经济增长和生态可持续性。
流域管理者在协同配置过程中会根据经济效益的变化选择相应的配置方案，图4-6和图4-7给出了模型配置方案与实际分水方案产生经济总值之间的变化。当单方污水经济效益的权重在［0.1，0.25］和［0.7，0.9］时，模型配置方案中流域产生的经济总值低于实际配置方案产生的经济总值；当单方污水经济效益的权重在［0.25，0.7］之间时，流域配置方案明显高于实际配置方案的经济总值。这是由于当单方污水经济效益的权重在［0.1，0.25］和［0.7，0.9］时，协同配置之间的冲突依然存在不对等的情况，流域水资源管理者对公平性和经济效益总有不同的偏好，使得协同配置之间的冲突加剧，导致配置方案产生的经济总值低于实际配置方案产生的经济总值。然而，当单方污水经济效益的权重在［0.25，0.7］之间时，协同配置中公平性与经济效益的权重处于相对均衡的状态，使得协同配置的效率最高，此时配置方案的经济总值高于实际的经济总值，由此表明协同配置将有效提高流域总体经济。
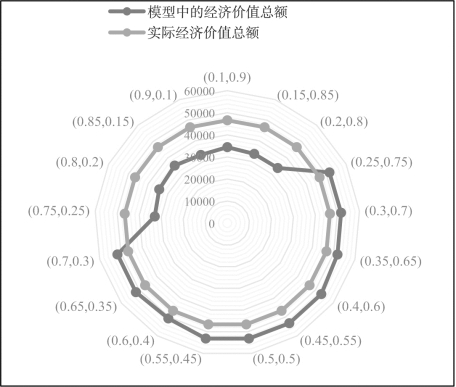
图4-6 分配方案产生经济值与实际经济值
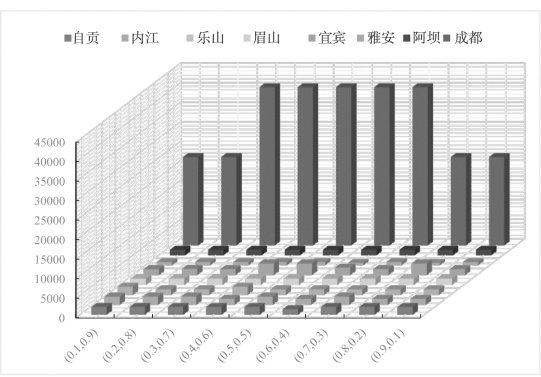
图4-7 配置方案中各区域总体经济
实际分水方案中，流域管理当局并没有考虑我们模型中设定的两个目标，所以，权重的变化对实际分水方案没有变化。图4-8表明了配置方案中各个区域之间的经济总值与实际经济总值在不同权重集下的变化。通过各个区域之间的经济总值与实际经济总值的对比，制定符合各个区域的配置方案，以保证流域区域产生的经济效益最大。（a）成都市的配置方案最具代表性，呈现中间高两边低的变化趋势，变化趋势与流域总体变化趋势相符合，这是由于岷江流域中成都市的实际经济总值大于其余城市的经济总值之和。值得注意的是，成都市的配置方案产生的经济总值在不同权重集下，成都市经济总值大于实际经济总值，主要是因为成都拥有更好更集中的工业和服务业，经济发展迅猛。（b）自贡、内江、眉山、阿坝这几个市的配置方案产生的经济总值均高于实际经济总值，其中阿坝在协同配置中的经济总值变化程度最大，主要得益于这几个地区着重发展轻工业和旅游业，为区域经济发展提供了有力支撑；（c）乐山、宜宾和雅安的配置方案中有部分权重集产生的经济总值低于实际经济总值，主要是因为“十三五”规划时期这几个地区集中发展重工业，致使环境污染严重，环境治理成本较高。
根据上述分析，在协同配置下的分配方案会使得流域经济总值增加，但是有部分权重集下的区域的经济总值会减少，这需要流域管理者根据各个流域的实际情况选择最佳的配置方案，使得流域总体经济效益最大的同时，各个区域的经济总值也能够得到相应的提高或者为了流域经济发展而使得经济总值减少最小。另外还需要考虑流域污水治理的成本的影响。但总体来讲，本研究的模型能够有效的缓解流域管理当局在协同配置方案中公平与效率之间的冲突。
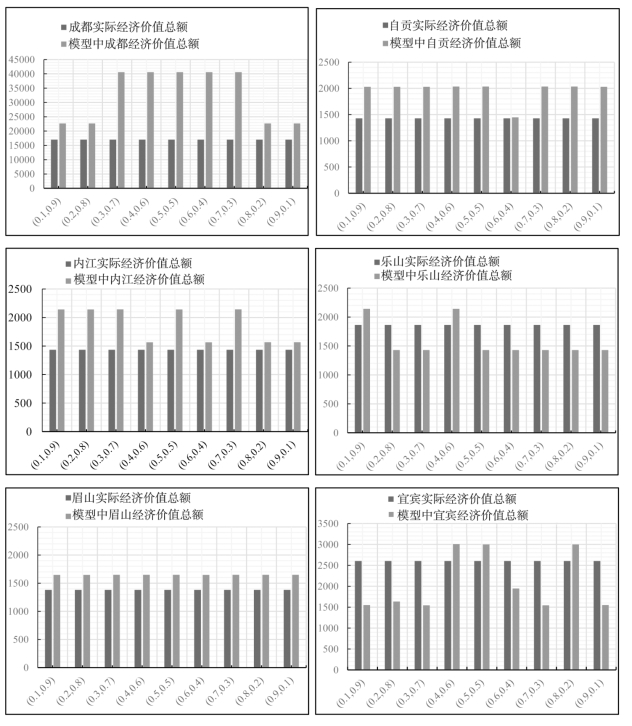
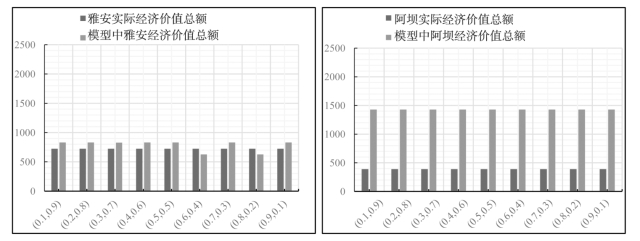
图4-8 配置方案中各区域经济与实际经济
流域管理者可以为经济效益和公平性这两个目标选择不同的权重。在这里我们将采用等权重（w1=w2=0.5）的方案作为基础，称为基本权衡决策方案（Basic trade-off decision scheme，BTS），此时经济效益和公平值达到图4-6和图4-4中的均值。等权重的水资源分配和排污权分配策略如表4-7所示。无论公平与否，当岷江流域管理者在以社会经济效益最大值为目标时，即追求经济效益最大化的决策方案（Economic benefitmaximization scheme，EBM），对应的水资源和排污权分配策略如表4-6所示。通过对比表4-7和表4-6，岷江流域管理者应该放弃37.56%的经济效益以实现排污权经济效益最大，单方污水需要产生的经济效益降低10612万元，各个分区的排污权分配为：成都8.32、自贡0.48、内江0.37、乐山0.39、眉山0.36、宜宾0.45、雅安0.16、阿坝0.02（亿立方米）。显然，8个分区之间的排污权差异很大。
表6 BTS水资源和排污权分配方案
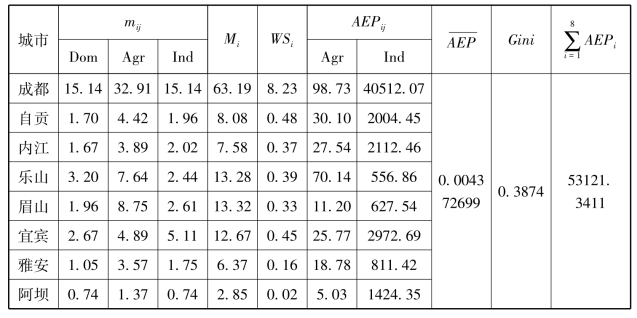
此外，EBM与BTS存在明显差异。两种方案的分水策略经济效益相差19953.7917亿元，其中BTS方案中的成都工业AEPij为40512.07元每立方米，EBM方案中的成都工业AEPij为22584.01元每立方米，两者之间相差44.25%。值得注意的是，实际上成都经济的总值大于其余岷江7市之和，这表明在考虑经济效用和公平性时，能够更加促进地区之间的发展而不是制约，同时EBM方案这在很大程度上对成都分区是不公平的，这表明BTS比EBM为区域发展提供的平衡更多，冲突更少。BTS方案在一定程度上是一种激励机制，强调社会公平，符合实际情况，同时也为相对落后的地区（包括内江和宜宾）提供机会。
表7 EBM水资源和排污权分配方案
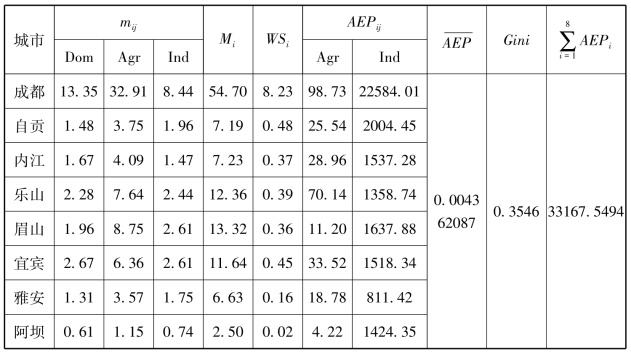
公平最大化决策方案（Equitymaximization scheme，EMS），表8列出了相应的水资源和排污权分配策略。将表6与表8进行比较，公平最大化时岷江流域管理者的经济效益效率应为34454.0503亿元，同时基尼系数小于BTS方案。虽然公平性得到改善，但经济效益下降约35.14%。水资源分配方案的经济效益下降18667.2908亿元，这对四川省的总体发展影响巨大，会严重降低经济GDP，这就是EMS方案在水资源配置方面不太可行的原因。社会经济对岷江流域发展十分关键，很明显，岷江流域管理者不能完全放弃18667.2908亿元的经济效益，BTS水资源和排污权分配方案在确保分区公平性的同时考虑到了社会经济。为了促进四川省岷江流域8市的发展，岷江流域管理者不应只考虑公平。
同时，通过EMS与BTS对比发现，BTS更加符合实际的显示流域经济效益，同时AEPij也更加符合四川省的发展规划，仅根据表4-7和表4-9计算的数据表明成都市的工业AEPij分别为40512.07和22584.01（元每立方米），乐山市的工业AEPij分别为556.86和2071.52（元每立方米），2019年实际成都工业GDP为17012.65亿元，乐山工业GDP为801.88亿元。显然充分考虑公平性和经济效益能够良好的反映实际情况，同时也能够对于污水排放应产生多少经济效益做出准确的测度，促进岷江流域8市通过减少污水排放以经济的正向循环。
BTS方案是根据经济效用和公平性制定的，能够提供更多的发展机会，强调社会公平，在一定程度上也是激励措施，能够为流域相对落后的地方提供发展机会。
EMS方案根据分水公平性最大化制定，能够有效解决分水不公平性的问题，但是会让流域遭受一定的经济效益损失。
EBM根据单方污水经济效益最大化制定的，能够带来更多的经济效益，相比于实际分水方案，会增加一定的经济效益，但是流域的分水公平性会相应的降低。
综上所述，我们的协同分配方案可以根据流域水资源管理决策者的偏好进行动态调整，当以公平性为主要目标时，可采用EMS方案；当以经济效益为目标时，可采用EBMS方案。
表4-9 EMS水资源和排污权分配方案
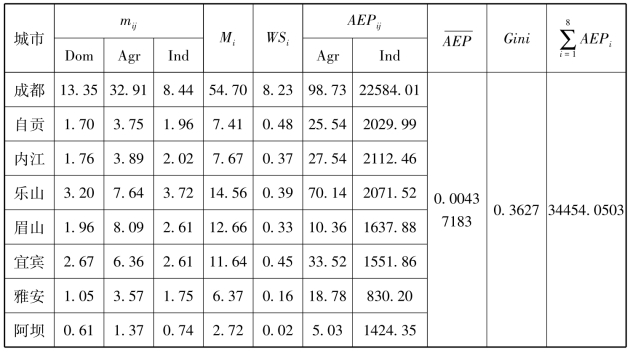
推动流域水资源优化分配，科学配置水资源是缓解流域水资源短缺和供需矛盾的重要途径。本文根据岷江流域单向、跨界的特点，将公平、经济效益和生态可持续性纳入了水资源的配置计划中，权衡了水资源配置公平合理性和污水排放之间冲突，并建立水资源配置的优化模型，该模型能够有效帮助水资源配置和污水排放之间的协同。模型表明，分水公平性和单方污水排放产生的经济效益之间的权衡是合理可行的。