多目标决策问题求解技术

二、多目标决策问题求解技术

多目标决策问题一般不存在唯一的最优解，在求得的解集中，我们称之为非劣解解集（帕累托最优解集）。因此，多目标问题的最终决策只能从帕累托最优解集中根据决策者偏好选出最优均衡解，尽可能的满足所有目标的要求。求解多目标决策问题的常用技术包括非劣解生成技术、离散多目标优化决策技术、连续多目标优化决策技术，这几种方法各有自己的特点和应用范围。本节将简要介绍几种方法。

（一）非劣解生成技术

非劣解生成技术是求解多目标决策问题常用的方法之一。其方法是首先将多目标优化问题通过一定技术手段将其转化为单目标优化问题，然后直接利用现有的单目标优化问题求解程序，生成多目标优化问题的非劣解解集。就非劣解生成技术而言，其适用性和实用性比较广泛，它既可以应用于个体决策、群体决策和不确定性条件下的决策，并且在求解的过程中，不需要决策者给出任何形式的偏好结构。这里我们只介绍权重扰动法和约束法。

1.权重扰动法

权重扰动法在多目标求解过程中根据客观实际和决策者的权衡将每个目标赋予相应的权重，然后将各个目标函数的加权和作为单一的目标函数，求出该单一目标函数的最优解即非劣解集中的帕累托最优解。通过设定不同的权重组合得到对应的解，最终生成非劣解解集。一般而言，这些权重均是经过标准化的，也即∑ωi=1。

这里我们将式（2-7）采用权重法可以转换成如下权重问题P（w）：

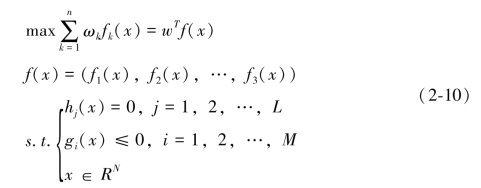
其中权重向量为：

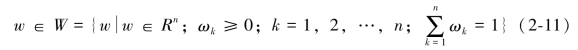
根据式（2-10）和（2-11）可知，在利用加权方法求解非劣解时，若给定权重向量w0，求解P（w）可以得到帕累托前沿解x0；如果x0是P（w0）的唯一解，或每一组wi是严格的正值（w＞0），于是可以证明x0是该多目标优化问题的一个帕累托前沿解。另外我们可以通过迭代求解过程，继续选择多组w来求解P（w），可以得到多个目标问题的若干个帕累托前沿解。这种情况对目标函数和约束集X是凸性的，可应用P（w）生成多目标问题的帕累托解集；否则，不能生成非劣解。另外，由于这种方法需要不断改变各个目标函数的权重值wi，因此也被称为权重扰动法。

基于权重扰动法，针对某些简单的多目标问题，一般可采用解析法来求解帕累托前沿解，即可以直接利用Kuhn-Tucker条件寻求前沿解。针对较为复杂的多目标问题，可利用数值法进行求解。下面将从案例来说明其具体应用。

1）解析法案例

例2.1 设如下多目标优化问题为

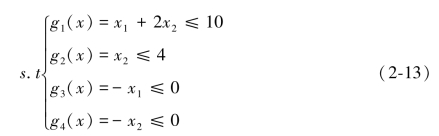
其中

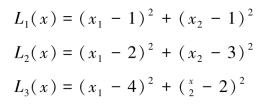
解：这里将采用权重法将多目标优化问题转化为如下权重问题P（w）：

且满足约束条件（2-13），其中，wi≥0，w1+w2+w3=1，i=1，2，3。

进一步将原极小值的优化问题转化为极大值的优化问题

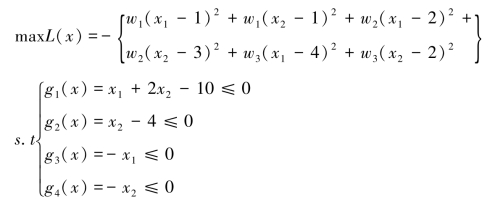
根据Kuhn-Tucker条件可以得到

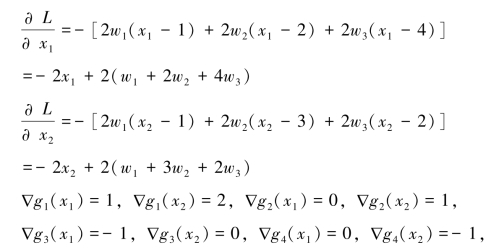
根据式（2-4）变化可得

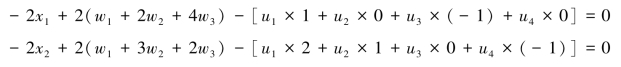
整理得到

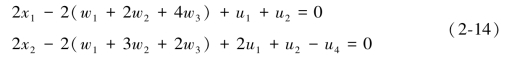
根据式（2-5）变化得

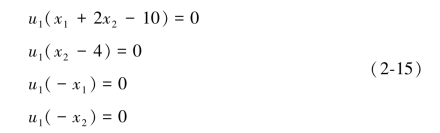
和x1+2x2-10≤0，x2-4≤0，x1≥0，x2≥0，其中μj，j=1，2，3，4为第j个约束的Kuhn-Tucker乘子。

对于这个特定的约束不等式问题，约束条件式（2-13）中没有一个对最优点是有约束力的。对wi和μj及w1+w2+w3=1，求解式（2-14）满足所有非负要求的解是不存在的。比如当x1=x2=0，则从式（2-15）中变化得到μ1=μ2=0，于是式（2-14）可转化为如下条件。

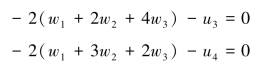
且当w1+w2+w3=1时，上式没有非负解。当式（2-15）有约束力时，那就意味着x2=0，x1=10。从式（2-15）中可以得到μ2=μ3=0，将这些值回代式子中，可以得到

那么则有

显然，这并不不满足0≤w≤1的要求。再作同样的分析可以得出，仅有可能的解是μj=0，j=1，2，3，4和

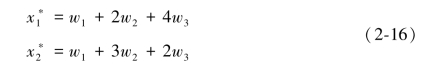
另外，我们假定

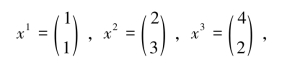
可以得到

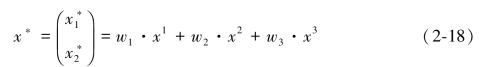
由于每个目标函数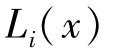，i=1，2，3均是凸性的，所以x可由方程（2-18）来确定，它就是的P（w）唯一解。当给定wi∈W时，x也是方程式（2-12）和（2-13）的非劣解，其非劣解集x*为式中所表示的凸集，即

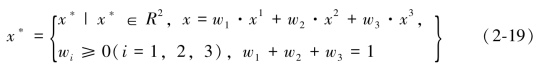
这个非劣解如图2-2所示：

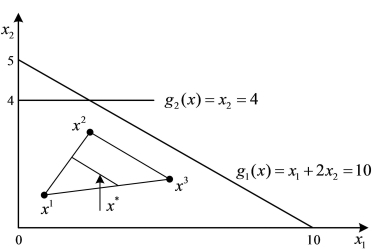
图2-2　非劣解图示

2）数值法案例

数值法在各个目标权重的可行域范围内，通过不断扰动权重值用以生成全部或有代表性的非劣解，从而供决策者选出均衡解。当目标函数和约束集合没有特殊要求（除凸性外）时，数值解法的程序一般是先将wi离散为0～1的有理数，然后对w1，w2，…，wp，的各种组合求解p（w）问题，从而生成原问题的非劣解。下面结合例来说明应用权重法数值解生成该问题的非劣解。

例2.2 已知如下多目标优化问题为

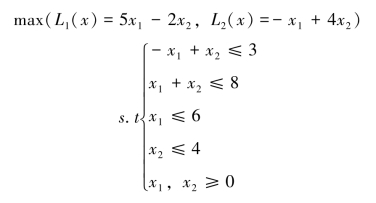
解：首先写出p（w）的问题

满足上述约束条件。

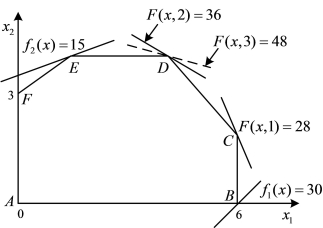
图2-3　权重法决策空间

其次分别优化各个目标，即在各处满足上述约束条件下求解L1（x）和L2（x）的最大值，并将其极值点B（x1=6，x2=0）和E（x1=1，x2=4）及相应的目标函数值L1=30，L2=-6和L1=-3，L2=-15分别绘于本例题的决策空间（图2-3）和目标空间（图2-4）上，其中过B点的线性无差异曲线，斜率为（-w1/w2）=（-w1/0）=-∝，是通过B点的垂直线；而过E点的线性无差异曲线是一条水平线，其斜率为（-w1/w2）=（-0/w2）=0，显然这两个单目标问题的解均是唯一的无劣解。

我们再次扰动权重值，一般将权重离散为0～1的有理数，也可以取任意的有理数。为了在目标空间确定线性无差曲线的斜率，取用权重值的相对值（即其比率w1/w2）才更有意义。为了简便起见，取L1的权重w1=1，则权重问题将成为

该权重问题满足原约束条件。

这里w1不再是权重目标函数的变量，因为它在这轮以后的迭代求解过程中是不变的。现在可任意选定w2的变化范围，如从0变化到3，这意味着将以（w1，w2）=（1，0）=（1，1）=（1，2）=（1，3）分别求解p（x）问题，然而当w2=0的情况已经求过，现在取w2=1，则问题（3-21）的目标函数为

满足约束条件，其解发生于图2-3中的C点，其值为x1=6，x2=2，L（x，1）=28，即L1=26，L2=2。这个结果也可对应地绘制于图2-3中，无差曲线的斜率为-1/w2=-1/1=-1，切于目标可行域边界线上的C点。

C点的线性无差曲线方程可从式（3-21）中导出

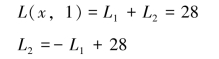
如图2-3所示

当w2=2时，权重目标函数为：

满足原约束条件。问题的最大值位于图2-4中的D点，其值为x1=x2=4，L（x，2）=36，L1=L2=36。对于w2=2的情况，L（x，2）=L1+2L2=36，无差异曲线为L2=-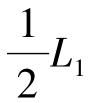+18，切于D点。

当w2=3时，权重目标函数为max？L（x，3），约束集不变。问题的最大值仍发生于D点，如图2-3和图2-4所示。

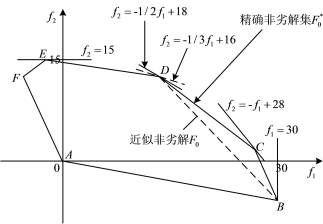
图2-4　权重法目标空间

最后进一步对非劣解进行校核。结果发现，只要7/5≤w2≤5，极值D点都是权重问题的最优解。假设w2值变化于0～4，并且每次增加两个数，即（w1，w2）=（1，2）=（1，4），C点将被溃漏，在图2-4中将出现BD连线的近似非劣目标解。这个近似解虽然是可行的，但对直实的非劣目标集（BCDE折线）而言，却是一个劣解。

显然，用这种方法生成非劣解全集，需要每次摄动权重值不能过大；否则，误差很大，所生成的非劣解可能不是真正的非劣解。还应指出，权重w必须是非负的；否则，负权重（-w）等于将原问题的最大换成了最小问题。当权重法用于生成非劣解集时，通过摄动不同权重值来生成不同的非劣解。但是，它只在非劣解集为严格凸集时才能全部生成。当它为非凸集时，非凸的那部分则不能鉴别。

2.转化约束法

（1）通过求解约束问题生成非劣解也是多目标优化问题的常用方法。约束转化法是从全体目标中选择一个最重要的作为主目标，把其余的目标函数都视作为约束条件。这样由主目标函数及此一组新增加的约束条件就建立一个单目标最优化求解模型来求解。

这种方法能生成全部的非劣解x*，至少在理论上，对非凸性和凸性问题都能适用。

约束法的最普通的形式记为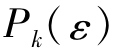

其中，εi为第i个目标的上限值i=1，2，…，p，i≠k。

设ε0为一向量，并且对问题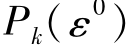是可行的。若x0是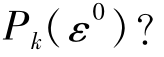（1≤k≤p）的唯一解，或对每个k=1，2，…，p，解Pk（ε0），则x0即为向量优化问题的一个非劣解。这就意味着向量优化问题中至少有某些非劣解能够通过求解Pk（ε）得出，其中只要ε的选取对Pk（ε0）是可行的。

换句话说，对任何给定的非劣解x*，对每个k=1，2，…，p也能找到ε，使得x0是Pk（ε）的解。这样的ε是由

给定的，其中

由于这种方法需将各个目标依次为基本目标，并相应地不断变动约束值εi，所以又称为扰动约束法。

约束法的解法也有解析法和数值法之分。解析法与权重解析法类似，首先将原问题写成合适的约束形式，然后应用最优性的必要条件（Kuhn-Tucker条件），通过分析求得多目标问题得非劣解集。这里只介绍数值解法。

（2）具体计算过程

约束法得数值算法得计算过程如下：

第一步：构造决策变量与目标函数值对应表。

（1）求解p个目标得各自极值，寻求各个目标得最优解，如第k个目标得最优解为；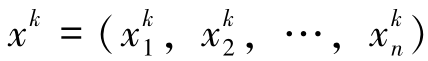

（2）计算每个目标值L1（xk），L2（xk），？，Lp（xk）（k=1，2，…，p）；

（3）排列各目标值于表（表2-1）中，其中得行相应于决策变量x1，x2，…，xp，而列标记为目标值。

（4）找出第k列得最大（或最小）值，记为Mk；找出第k列得最小（或最大）值，记为nk。对k=1，2，…，p均根据次步骤找出。

表2-1　p个目标得决策变量与目标值

第二步：找多目标问题转化为约束问题（3-22）

第三步：在第一步找到得nk和Mk中，表示出目标k在非劣集中得变化范围，即nk≤Lk≤Mk。这个范围就是ε得变化范围。然后，选择εk值得数目，以便用于生成非劣解，这里将εk不同值得数目记为r。

第四步：对εk，（k=1，2，…k-1，k+1，…，p）值得每种组合求解约束问题，这里

其中，εk值的组合数有rp-1个。若rp-1数目约束问题是可行的，则每一个约束问题均可产生一个非劣解（且这些目标约束是具有制约能力的），这些解均是非劣解集中有希望的近似解。

依目标函数和约束条件的特性，rp-1个约束问题可用适宜的数学规划去求解。下面举例说明。

例2.3 引用例2.2，应用约束转换法求解。

第一步：构造决策变量与目标函数值矩阵。首先，求解各个目标的最优解。目标L1（x）唯一解，其中x1=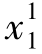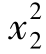（，）=（6，0），L1（x1）=30，L2（x1）=-6，目标L2（x）也有唯一解，x2=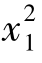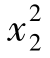（，）=（1，4），L1（x2）=-3，L2（x2）=15。它们对应值如表2-2所示。

表2-2　两个目标的决策变量及目标值

从表2-2中可以看出

第二步：建立约束问题。任选L1为基本目标，L2为约束条件，于是问题为：

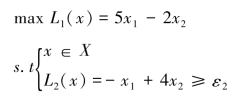
第三步：确定∊2值的变化范围。从表3.2中可知n2≤∊2≤M2或-6≤∊2≤15。∊2取值的数目r=4，即解约束问题共4次。由方程式计算∊2得

即为∊2=-6，1，8，15，求解约束问题4次。

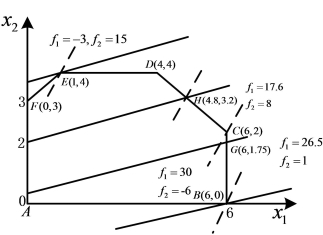
图2-5　约束法的决策空间

原问题的决策空间和目标空间的可行域如图2-5和图2-6所示。约束问题的简化形式也表示于图2-5和图2-6上。在两个空间中，约束问题有4个不同的可行域，即在4个ε2值中，每个值都有各自新的可行域。在图2-5中，当ε2=-6时，新的可行域恰好是X，即L2（x）切穿X于点（6，0）；而L2（x）在新可行域点（6，0）处达到最大。当ε2从-6增加到1时，相应于方程式向东北方向移动，当ε2=1时，可行域减缩为X的一部分，位于L2（x）=1处。此时，L1（x）的最优值位于新可行域上的点（6，1.75）。当ε2=8时，非劣解在点（4.8，3.2）处。当ε2=15时，非劣解点在（1，4）处。

约束法在目标空间的求解过程展示在图2-6中。新的约束呈现为水平线。目标L1（x）的最大值在L2（x）=1的水平线与原非劣解集边线相交处，即L1（x）=26.5。当L2（x）=6和L2（x）=15分别为两个界限时，L1（x）分别等于30和-3。当L2（x）=8时，L1（x）的最大值为17.6。

应该指出，当∊2的取值间隔较大时，像权重法一样，约束法求得的非劣解集也是有误差的，如图2-6中的点线所示。然而，约束法与权重法求得的近似解是差别的。约束法并不是在非劣值的极点处求得非劣解，因为原可行域已被修正，而在权重法中，可行域是不变的。

以上两节所介绍的权重法和约束法具有简单直观的优点，是求解多目标优化问题的基本方法。但是这两种方法中，不管哪个方法，计算量均是很大的，因为这两种方法均必须对各个目标依次选为基本目标进行重复计算，其计算量随目标数目的增加而呈指数形式增加。若用N个权重系数wi或N个上限值εi，目标个数为P，则需求解的单目标问题的数目将达S=NP-1个。因此，上述两种方法一般用于P=2或3，当目标多于三个以上时，不仅计算量很大，而且失去了非劣解集的图示分析的优越性。

（2）离散多目标优化决策技术

上面我们介绍了非劣解生成技术，它是一种比较客观的多目标求解方法，在针对有优先结构次序的多目标求解而言，决策者存在偏好次序，在作出最终决策时，对某些目标存在一定的偏好。本小节讲解的多目标问题决策技术，完全依赖于决策者偏好的决策信息，以便做出最终的均衡决策。

对于决策者的偏好信息获取，存在两种方式，一种是交互式的，一种是非交互式的。交互式是指在决策过程中，分析者和决策者始终互相传递信息，保持信息迭代更新，逐步获取决策者的偏好信息结构，最终做出满意的决策；非交互式是指决策者在决策过程中只给出一次性的偏好结构，也即给出了多目标的优先级。本节所讲解的多目标决策技术均是从非交互式角度来进行求解。然而，我们知道多目标决策问题中，决策变量既可以是离散的也可以是连续的，决策变量离散情况下的决策方案是有限的，其决策方法主要包括加权决策法、方案初选法和基于理想点法等。在讲解这些方法之前，先介绍决策矩阵和属性的规范化方法。

1.决策矩阵和属性的规范化

在工程实践中，例如工厂选址、商业产品评价、路径规划等问题属于方案有限的决策。这类问题的决策一般根据多种需求和准则进行综合评价和排序，最终根据决策者根据偏好信息选择最优的决策方案。例如，从水污染管理角度来看，需要从经济、社会、生态环境等方面对所有方案进行全面客观的描述和评价，最终根据评价结果在多种可行方案中选出最合适的方案。

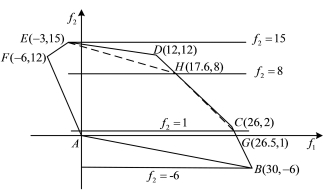
图2-6　约束法的目标空间

1）决策矩阵

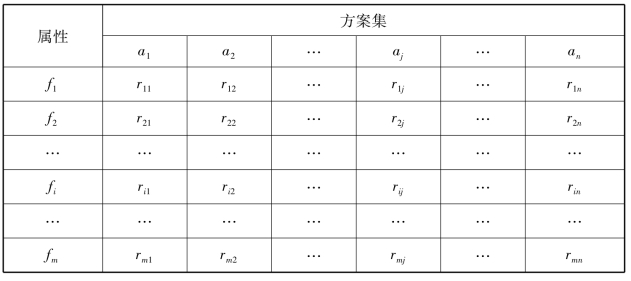
设A是一个离散的可行的有限方案集合，即A={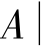A=aj， j∈［1，n］，n≥2}，fi代表第i个属性由各个方案所产生的值所组成的向量，即fi=（ri1，ri2，…，rin），i=1，2，…，m，其中rij表示第i个属性第j个方案的水平，其决策矩阵表示为表2-3所示，该矩阵的作用是为决策分析提供基本数据信息，是各种评价分析方案的基础。

表2-3　决策矩阵

在实际工程、管理等问题，不同方案的结果因指标不同等原因并不总是能够对两两方案进行直接比较，只能根据决策者偏好对方案进行优选和排序。然而决策者可能对某一属性值存在一定的偏好判断能力，但在做最终决策时无法根据属性值对方案进行满意度筛选，在这种条件下，如何对方案作出最佳选择呢？

2）属性的规范化

对于不同的方案比较，其指标等数据具有不同的量纲。决策者很难对不同的目标进行重要性排序。为了将不同量纲的多目标决策进行有效比较和分析，需要将各个目标进行归一化（标准化）处理，并把所有属性值或者目标值映射到［0，1］区间上，以消除量纲的影响，这就是所谓的规范化。这里将介绍几类常用的规范化方法。

①线性比例变换法

这种方法主要是将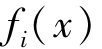视为向量，变换的核心就是将向量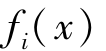中的所有分量去乘以该向量中的“最大分量”的倒数，若该向量是正向（属性值越大越好）目标，其变换如下：

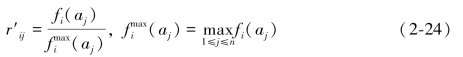
若是针对负向（属性值越小越好）目标，其变换应为：

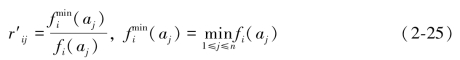
从上式我们可以看出，比例变换无法满足消除量纲和归一化的需求，并且能保证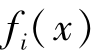中的最好值为1，最差缺不等于0。

②非线性比例变换法

非线性比例变换法是将属性之差按照一定比例进行归一化和无量纲处理，也会根据正向指标和负向指标进行处理。

其中正向指标的变换为：

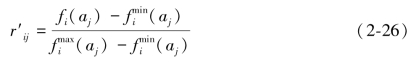
负向指标的变换为：

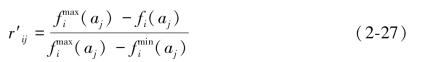
显然，非线性比例变换方法能够将不同目标之间的量纲归一化处理，不仅能够有效保障最优属性值为1，并且能够使最差属性的值为0。但是这种变换是不能将各个属性值（目标）按照一定比例进行变换，也只有变换后的r'ij具有相对值的意义。

2.加权决策法

方案集经过初选以后，被保留的方案还需要进行决策分析，以最终得到一个满意解。加权决策法便是一种用来进行这种决策分析的常用方法。加权决策法和第3章介绍的加权法有所不同，后者要求权重预先给定，前者则通过一定的客观事实，在决策者偏好的基础上，计算各因素的相对重要性次序的权重，然后根据权重对方案进行排序。本节介绍层次分析法（analytical hierarchy process，AHP）和权重调查方法。

①层次分析法

层次分析法是美国运筹学家、匹兹堡大学教授Saaty在20世纪70年代初提出的。它的特点是把复杂问题中的各种因素通过划分相互联系的有序层次使之条理化；根据对一定客观现实的主观判断（主要是两两比较），将每一层次引述的相对重要性进行定量描述；利用数学方法确定反映每一层次全部因素的相对重要性次序的权值；通过所有层次之间的总排序，确定所有方案的排序。

②层次分析法基本原理

首先将复杂问题层次化，构造一个递阶分析的结构模型，如图2-7所示。最高层表示总体目标；中间层（可能不止一层）表示具体目标或准则层；最低层为选用的评价因素，或措施，或方案层。

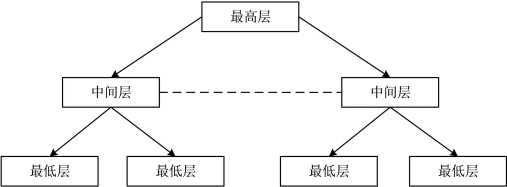
图2-7　递阶加权层次结构示意图

建立模型后，问题即转化为层次中的排序计算问题。将每层的排序计算问题简化为一系列成对因素的判断比较，并根据一定的比率标度将判断定量化，形成比较判断矩阵。通过判断矩阵的最大特征值及其特征向量，可计算出某层次因素相对于上一层次中某一因素的相对重要性权重，这种排序计算称为层次单排序。为了得到某一层次相对上一层次的组合权重，可用上一层次各个因素分别与下一层次各个因素相互比较判断的准则，得出下一层次因素相对上一层次因素的相对重要性权值，然后用上一层次因素的组合权值加权，即得到下一层次因素相对上一层次整个层次的组合权值。这种排序计算称为层次的总排序。依次沿递阶层次结构由上而下逐层计算，即可计算出最低层次元素相对于最高层次的相对重要性权值，或相对优劣的排序值。

③层次分析法基本步骤

层次分析法的基本计算步骤如下，

i.明确问题和建立层次结构。将系统的影响因素（自标，可行方案等）分门别类。层次结构是指根据系统中各因素的特点，将其分成不同层次。按照最高层、若干有关的中间层和最低层的形式排列起来。对于决策问题，最高层表示解决问题的目的：中间层表示采用某种方案实现预定目标所涉及的中间环节，中间层根据问题的复杂程度还可分为多个层次，如策略层、约束层和准则层等：最低层表示解决问题的可行方案。

相邻层次之间一般各元素只有部分发生联系。也就是说，不是某一层次的一元素与相邻层次的所有元素都发生联系。

ii构造判断矩阵

因素的两两比较是用来获取决策者的偏好信息的一种比较实际的手段，AHP方法要求决策者对每一个层次的各元素的相对重要性作出判断。这些判断用数值表示出来就是判断矩阵，它是AHP方法的信息基础。AHP方法中的判断矩阵是指针对上一层次的某一元素，本层次有关元素之间的相对重要性。

iii层次单排序及一致性检验

所谓层次单排序就是针对上一层次某个元素得到的判断矩阵，计算本层次与之有联系的元素的权值。这些权重反映了这些互有联系的元素的相对重要性。基本思路是首先根据判断矩阵计算各元素的权值，然后检验判断矩阵的一致性。

iv层次总排序并择优

如前所述，层次单排序的意义是针对上一层次的某一元素而言，本层次有关元素之间的相对重要性。而所谓层次总排序则利用同一层次中所有元素的单排序结果，计算针对上一层次所有元素而言本层次所有元素的权值。这些权值反映同层次各元素之间的相对重要性。

层次总排序的思路是从上到下按顺序逐层进行排序，对于最高层下面的第层（次最高层），层次单排序就是总排序。

④方案初选方法

对于离散多目标决策问题而言，行动方案是已知的。这些方案并非都是非劣的。在应用决策方法求取满意方案之前，应发现并剔除那些明显劣的方案，以减轻决策分析的负担。这里介绍优选法、连接法和分离法等几种初选方案的方法。

（1）优选法

优选法直接应用非劣的定义剔除劣方案，其基本思路如下：若对于一属性，方案A优于方案B，并且对于所有别的属性，方案A均不劣于方案B，则方案B是劣方案，应剔除。

这种方法能剔除决策问题中所有的劣方案，下面要求确定各属性的权重，并且无须对属性值进行规范化。但这种方法不能体现决策者的偏好，即不能在非劣解中作任何取舍。例如，某个非劣方案中某些重要属性的取值较差，此法也不会将其剔除。

（2）连接法

这种方法考虑了决策者的偏好。它要求决策者对每个属性都提供一个能接受的下限值，称为剔除值。只有当某个方案对应的每个属性均不低于相应的剔除值时，该方案才不被剔除。

应用这种方法进行决策的例子很多，如大学生每门必修课的考试成绩不能低于60分；企业生产计划中每项经济指标不能低于规定的值，超奖少罚，这些都是规定剔除值的例子。这种方法自然存在片面性，也就是属性之间不能补偿。按照这种思路，一个方案只要它对于一个属性的值没有超过给定的剔除值，那么无论它对于别的属性取什么值，都不能将它作为可取方案进行考虑。例如，一位作文水平相当高的学生，可能因为数学成绩没有超过60分而失去深造的机会。

（3）分离法

这种方法也要求对每个属性提供一个剔除值，但与连接法的需求相反，它规定某一方案只要对于一个属性超过了该剔除值，就保留该方案。

例如，在选拔人才的决策问题中，有时规定有一技之长的人都可录用，这种选拔人才的方法就是分离法，它适合于用来选拔特殊的专门人才、冒尖的人才等。但是，这种选才的方法仅考虑了一技之长，而忽视了其他方面的缺点，并且平均发展的人不被重视。因此，分离法也有片面性。

（4）基于理想点法

Hwang于1981年第一次提出基于理想点的排序方法，随之被广泛应用于决策中的优化问题。该方法首先需要决策者根据实际问题定义一个理想方案（可能该方案不成立），将各备选方案与正负理想解的距离进行比较，以靠近正理想解和远离负理想解两个评价依据为基准，对各个待评方案进行排序并作出最优决策。

①基本原理

基于理想点方法（Technique for Order Preference by Similarity to Ideal Solution，TOPSIS）的基本思路是定义决策问题的正理想解和负理想解，并给定一种距离度量技术，依据度量技术去测度每一种方法与正理想解和负理想解的距离，该距离越靠近正理想解，则说明该方案最优。

正理想解是一种假定的偏好方案，简记为A+，它往往是不成立的，并要求A+所对应的各个属性的值至少达到各个候选方案中的最好值。负理想解是一个假定的最坏方案，简记为A-，它往往也是不成立的，且一般要求A-所产生的各个属性值都至少不优于各个可行方案中的最坏值。为所有方案排序的决策规则就是把实际可行解与正理想解和负理想解进行距离测度，若某个方案可行解最靠近理想解同时又远离负理想解，则此解是方案集的满意解。

②距离度量

为了度量可行方案靠近正理想解和远离负理想解的程度，需要采用一定的距离测度。基于理想点的决策方法采用了几何度量的测度手段来刻度相对接近距离。

几何距离测度。几何距离测度是通常的距离概念，包括欧式距离、切比雪夫距离等测度手段，当采用这种度量手段时，往往会碰到某个解尽管离正理想解最近，但是不能保证离负理想解远，致使决策结果不客观准确。

相对贴近测度。假定决策问题有m目标函数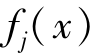，j=1，2，…，m，存在n个可行方案Ai，i=1，2，…，m，并设定该问题的规范化加权目标的正理想点为Z+=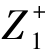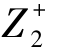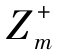（，，…，）T。用欧几里得范数作为距离的度量，于是任意可行解到正理想点的距离可以表示为：

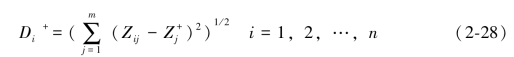
这里Zij为第j个目标对于第i个方案的规范划权重值。

类似的，可以定义任意可行解到负理想解之间的距离。设该问题的规范化加权目标的负理想点Z-=（，，…，），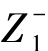

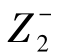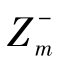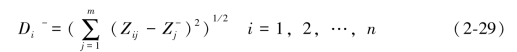
于是，针对任意可行解的相对贴近度定义为：

显然，0≤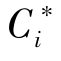≤1，i=1，2，…，n，当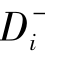=0时，Ci=0；当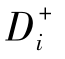=0时，Ci=1；所以Ci越大，表明评价方案离正理想解的距离越小，离负理想解的距离越远，因而其评价结果较好。

③基于理想点法算法步骤

第一步 设多目标问题的决策矩阵为X。由X可构成规范化的决策矩阵为Z'，其中的元素为Z'ij。

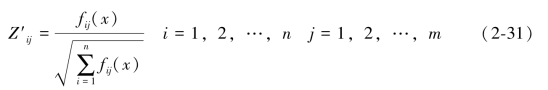
其中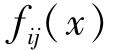由决策矩阵给出。

第二步 构造规范化的加权决策矩阵Z，其中元素为Zij。

其中 j为第j个目标的权重。

第三步 确定正理想解Z+=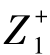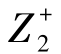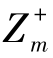（，，…，）T和负理想解Z-=（，， …，）。

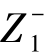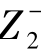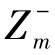第四步 计算每个方案到理想点的距离和每个方案到负理想点的距离。

第五步 根据相对贴近度公式计算每个方案接近理想点的相对贴近度。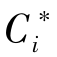

第六步 根据每个方案的相对贴近度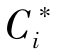的大小对方案排序并做出决策。

（3）连续多目标决策问题

多目标决策是对多个相互矛盾的目标进行科学、合理的选优，然后做出决策的理论和方法。它是20世纪70年代后迅速发展起来的管理科学的一个新的分支。多目标决策与只为了达到一个目标而从很多可行方案中选出最佳方案的一般决策有所不同。

常用的方法有下述几种；

1.化多为少法。即将多目标改为由一个统一的综合目标来比较方案。包括综合评分法、平方和法及约束法。

2.目标分层法。把所有目标分别按其重要性排一个次序。

3.分层序列法：将所有目标按其重要性程度依次排序，先求出第一个最重要的目标的最优解，然后在保证前一目标最优解的前提下依次求下一目标的最优解，一直求到最后一个目标为止。

4.直接求非劣解法：先求出一组非劣解，然后按事先确定好的评价标准从中找出一个满意的解。

5.目标规划法：对于每一个目标都事先给定一个期望值，然后在满足系统一定约束条件下，找出与目标期望值最近的解。

6.多属性效用法：各个目标均用表示效用程度大小的效用函数表示，通过效用函数构成多目标的综合效用函数，以此来评价各个可行方案的优劣。

7.层次分析法：把目标体系结构予以展开，求得目标与决策方案的计量关系。

8.重排序法：把原来的不好比较的非劣解通过其他办法使其排出优劣次序来。

连续多目标问题的主要特点有：

（1）是具有多个目标的有限个决策变量相互制约的问题。

（2）多个目标函数以及多个决策变量之间具有已知的函数关系表达式。

（3）由多个约束条件组成的可行域中，存在无限多个的可行方案。

将已知目标函数均取最小时，连续多目标问题可由以下定义：

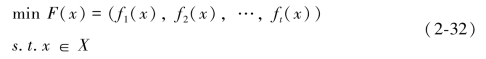
x=（x1，x2，…，xn）T表示以上连续多目标函数的决策变量，X表示可行域，F（x）=（f1（x），f2（x），…，fn（x））表示目标函数。

与离散多目标问题类似，以上连续多目标问题通常情况下无法找到其最优解，一般情况下只能得到该问题的非劣解。若目标函数对应的价值函数表示为V，那么以上连续多目标问题的非劣解就对应下列单目标数学规划问题的最优解，即：

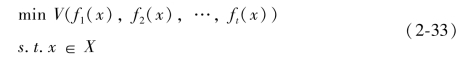
由以上描述可以得出：在已知多目标决策问题的价值函数的前提条件下，就可以减少对其他多目标决策方法的研究。然而，通常情况下，研究者得到的并不是对应价值函数的显式表达式，而时隐式的，此时，就需要根据已知信息利用不同的途径寻求决策者的偏好信息。并且可以把求解连续型多目标决策问题描述为以下一般问题：

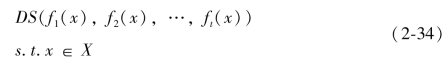
其中，DS表示决策者在不同偏好信息条件下选择的适当的决策方法，并在可行的方案集X中寻求一个满意解。

4基于整体偏好的方法

（1）交互式方法

交互式决策方法一般都具有这样的特点：即在问题求解过程中，这类方法是需要决策者与决策分析者进行不断地对话，持续地参与决策过程，在决策者和分析者的相互作用中，逐步获得决策者的偏好结构，最后得到令人满意的决策。并且由于描述决策者偏好的具体方式不同，可以利用置换率或参考点等形成多种不同的决策方法。

交互式决策方法的一般步骤如下所示：

（1）明确需要决策的问题，并将问题用数学模型进行描述。

（2）对于现有的决策问题，求出一个决策者比较偏好的可行的非劣解。

（3）与决策者交换信息，征求决策者对当前解的意见。

（4）如果决策者很满意当前解或者决策过程的终止判断被满足，当前解为现有决策问题的最佳调和解，此时决策过程结束。否则，将按照下述步骤持续进行。

（5）根据决策者的意见对决策方法进行调整、修改，求出在相应偏好下比较好的非劣解，返回第（3）步。

（2）均衡规划

均衡规划方法是连续多目标问题求解中常用方法之一。一般，应用该方法需要明确三个量：（1）决策者对决策问题偏好的权重大小，用ω来表示；（2）理想向量f*；（3）与理想点的测度标准Ll，l为其参数。

为了方便描述，我们将理想向量定义为：F*=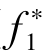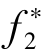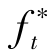（，，…，），其中的任一单理想向量是由求解下述问题得到：

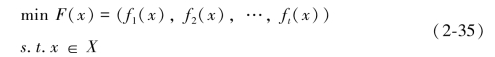
若对以上t个目标函数都在x*处取得可行域内的可行解，那么F*=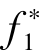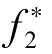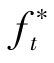（，，…，）则为该连续多目标问题的最优解，然而，这种情况一般是极少见的。因此，研究者通常是把该理想解当作是对非劣解的估算标准。此时，求解连续多目标问题就转化为了求解最接近理想点的可行解集，并从中挑选出符合实际问题的一个解。

那么，如何测量非劣解是否接近理想点呢？常用的测度标准为一族度量标准Ll，它是对距离的一种几何刻画。当l=∞时，Ll叫做切比雪夫范数；当l=2时，Ll叫做欧几里得范数；当l=1时，Ll叫做绝对值范数。Ll还有以下两种表达方式：

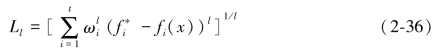
或者

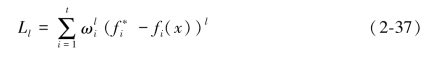
并且1≤l≤∞。

若已知连续多目标决策问题有权重向量ω=（ω1，ω2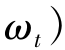，…，，并将该问题的均衡解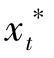作以下解释：

式（2-33）的均衡解通过给定的权重集ω=（ω1，ω2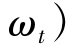，…，对1≤l≤∞进行求解与计算。令ω1=ω2=…=ωt=1，并设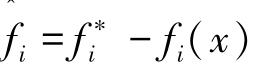，此时（2-33）可以表示为：

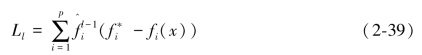
特殊的，当l=1时，有：

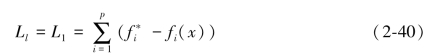
此时，我们的目标实际值与理想值出现的偏差就是相同的了。

类似的，当l=2时，多目标问题：

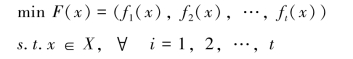
转化为：

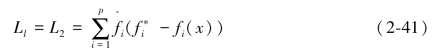
由于每个偏差权重的选取与其大小关系是相对应的，即我们选择的偏差越大，那么权重即越大。并且可以发现，当l的取值越来越大直至趋于无穷时有：

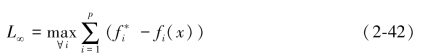
等式（2-41）可以清楚的反映出l的选择来源于决策者对最大偏差的偏好，l越大，说明决策者更关注最大偏差的情况，对权重大展现出来的情况更为关心。

在式（2-35）与式（2-36）提出度量决策者对不同目标重要性选择的偏好下，可以将式（2-35）和式（2-36）展示为：

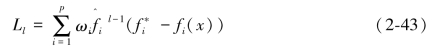
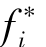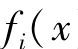（-））通过对l的选择按照比例变化，目标权重按照l次幂变化，直到当l取到无穷的时候，此时即：

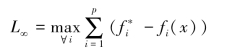
但其实，我们在实际计算过程当中，需要对几个目标函数的偏差范围有一个衡量，即规范化目标函数的偏差，用式子代表，就相当于用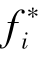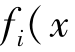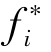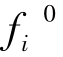（-））/（-）来代替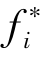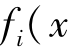（-）），这样可以保证各目标函数具有相同的范围，并且可以清楚地知道，该范围控制在（0，1）区间内。

下面，我们对f0作一个解释，f0是由下面这个式子计算出来的：

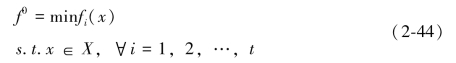
其中，X*作为x的非劣解集，可以将式子（2-37）改写为：

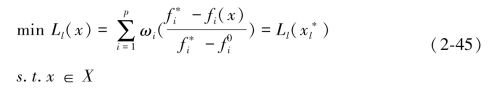
在求解式子（2-45）时，对于任意一个l满足1≤l≤∞，存在非劣点；当l取l=∞时，此时就至少有一个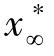是非劣解，若将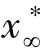当中的非劣解放在均衡解集当中，那么均衡解集就是属于非劣解集X*的。决策者理想的均衡解就可以在这个子集或均衡集当中来进行。若决策者能够在该解集中寻找到满意解的话，寻找理想点的过程结束；否则，要将不满足找到满意解的解集进行重新定义，对理想点进行重新定义，直至找到决策者想要的最佳均衡解为止。