“同时”的相对性

假定在一个惯性系S中，有相隔一定距离的两点A和B，在AB的中点O处有一光源。在某一时刻，我们让光源发光，它发出的光同时向A、B两点传去。由于AO=BO，而且光速对于惯性系S来说，总是c，所以光到达A点和B点的时间相同，也就是说“光到达A点”和“光到达B点”这两件事，对惯性系S中的观察者来说，是同时发生的。这没有问题。

现在假定有一个相对于S做匀速直线运动的惯性系S′，运动方向是向右，速度为v。在S′中，也有相隔一定距离的两点A′和B′，A′B′的中点O′处也有一个光源。当这个光源发光时，在S中的观察者看来，将会发生些什么情况呢？

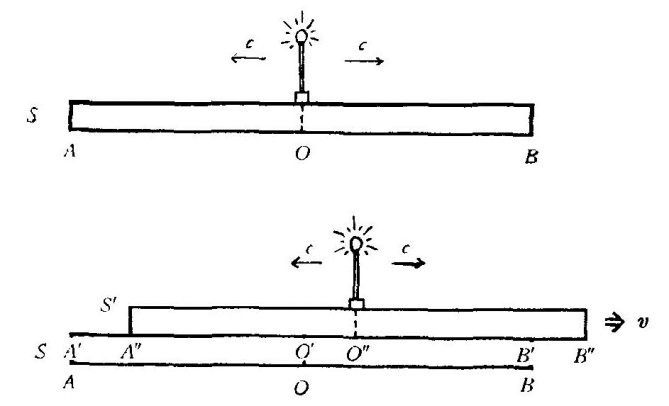
首先，这个光源发出的光向B′点传去时，其光速对于S来说，仍然是c，虽然S′相对于S有一个速度v。这一点至关重要，因为在牛顿的经典力学中，这个光速是c+v，但在相对论中，由于光速不变原理，它仍然是c。同样道理，光向A点传去的时候，它相对于S的速度也是c，而不是c-v。

其次，由于光的传播需要一定的时间，所以当光在空中传播的时候，B′点向右运动到了B″点。因此，在S中的观察者看来，光走过的路程是O′B″=O′B′+B′B″。同样道理，光向A点传去的时候，它走过的路程是O′A″=O′A′-A′A″。由于O′A′=O′B′，故显然O′B″＞O′A″。

由于光的传播速度都是c，所以光到达B″点所花的时间比到达A″点所花的时间长。也就是说，对于S中的观察者来说，“光到达A″点”这件事发生在“光到达B″点”这件事之前。

如果S′中也有一位观察者，他跟着S′一起运动，他怎么看呢？在他看来，S′是不动的，A′与A″、B′与B″是一回事，光速对于他来说也是c，而且又有O′A′=O′B′。因此他的情况同S中的观察者当初观察自己惯性系中的情况一样，“光到达A′（A″）点”和“光到达B′（B″）点”这两件事是同时发生的。

你看，同样的两件事，在一个惯性系看来是同时发生的，但从另一个惯性系看却不是同时发生的。相对论中的光速不变原理给我们带来了与日常经验如此大相径庭的结论，这就迫使我们不但要抛弃绝对空间的概念，而且要抛弃绝对时间的概念。

我们比较习惯于空间的相对性，即上下、前后、左右这些空间位置要根据观察者本人的情况而定。但是，对于时间我们一直认为是绝对的。两件事是不是“同时”发生的，这是能“绝对”确定的，不会因人而异。现在，相对论告诉我们，时间坐标跟空间坐标一样，也是相对的，没有一只适用于一切惯性系的绝对的“钟”。每个惯性系都必须用自己的“钟”来测量属于本参考系的时间坐标，以此来判断两个事件发生顺序的先后。时间的相对性是相对论给我们最深刻的启迪之一。