尺缩短，钟变慢

据说少年时代的爱因斯坦一直在考虑的一个问题是：跟着光线跑人们会看到什么景象？直到几十年之后，人们才认识到这个问题的涵义有多么深刻：当你以接近光速的高速作匀速直线运动时，世界的图景在你看来将是异乎寻常的。

这时，你去测量（注意，是“测量”而不是“看”）一把沿着你运动方向静止放置的尺的长度l2，会发现它竟比日常所见的长度l1（即你不做高速运动时所测量的长度）缩短了不少。两者的关系为：

式中的v是你做高速运动时的速度。你跑得越快，测量下来那把尺就越短。这时，圆和正方形测量下来将变成竖放着的椭圆和长方形。原来测量下来是1米长的木棍，这时测量下来也许不到0.6米了。

与此相仿，时钟也走得慢了。原先12小时走一圈的时针运动，现在用你的钟来计量竟要花12小时以上。因为按照相对论，一件事的发展过程（例如，时针走一圈）原来需要花费时间为t1，现在该事件发生所在的惯性系从原来的静止状态变成以速度v相对于你做匀速直线运动状态（运动是相对的，你在做高速运动时，原来静止的钟相对于你以相反方向做高速运动），此时，这件事的发展过程所需时间你测量下来就变为t2，两者间的关系为：

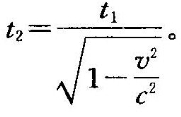
由于世界上没有比光速更快的速度了，因此，v总是小于c，从而1-总是小于1的正数，这样，l2总是小于l1，t2总是大于t1。换句话说，物体相对于你运动时总是在运动方向上发生长度缩短，时钟相对于你运动时总是变慢。惯性系相对于你运动的速度越快，放在里面一起运动的物体在运动方向上的长度你测量下来就越短，放在里面一起运动的时钟你测量下来就走得越慢。当它以接近光速的高速飞驰时，“山中方数日，世上几千年”之类的神话将变成现实。

尺缩短，钟变慢，这一切真的会发生吗？在我们日常生活中这种现象简直是天方夜谭，可是在高能物理中，由于高能粒子常常以接近光速的速度运动，诸如此类的相对论效应是屡见不鲜的。例如，用高能质子轰击某种靶时，会产生高能π介子。实验表明，π介子静止时，它的半衰期是1.77×10-8秒。而当高能π介子以0.99c的高速运动时，它的半衰期长达13× 10-8秒。这表明，高速运动着的高能π介子要比静止时的π介子“长寿”得多。