从刘徽割圆谈起

你一定知道圆周率π，它是圆的周长与其直径的比值，近似地等于3.1416。但π的这个近似值是怎样求出来的？这你或许就不一定知道了。在现代数学的一个专门分支——计算数学中，有许多有效的计算π的方法，但它们一般都要涉及到一些高级的数学概念。其实，有一个既直观又初等的方法，那就是我国魏末晋初时期的数学家刘徽所用的割圆术。

刘徽割圆术的基本思路是这样的：

假定有一个直径为1的圆，计算圆周率就相当于求这个圆的周长。那么怎样来求这个圆的周长呢？我们可以先画一个边长为1/2的正六边形，显然，它内接于直径为1的圆。然后作正六边形各边的垂直平分线，这些垂直平分线当然经过正六边形的中心。以中心为一个端点，在每条垂直平分线上各截取长为1/2的线段，这样，这些线段的另一个端点（共6个）连同正六边形的6个顶点就成为一个正12边形的顶点。再对这个正12边形重复上面的做法，就可以得到一个正24边形。依此类推，我们可以继续得到正48边形、正96边形、正192边形、正384边形……只要有时间和耐心，我们可以一直做下去。从图形上看，这些正多边形是越来越接近那个直径为1的圆了。因此我们可以用边数足够多的正多边形的周长来近似地作为那个圆的周长，而这些正多边形的周长是可以从最初的那个正六边形周长（等于3）开始，用勾股定理一步一步地计算出来的。

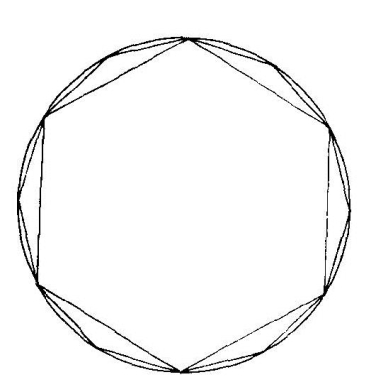
刘徽割圆术

据说，刘徽用这种方法算到正192边形，得到了圆周率π的一个近似值3.141024。这在当时是一个了不起的成就。