3.3 主谐振网络及输出电路
压电变压器的主谐振网络呈现线性带通特性。这里压电变压器不仅起到变压隔离的作用,同时也是限制电能变换和能量传输的主要元件。由其频谱特性知,当网络是一个高Q值的谐振网络且开关驱动频率比较接近于系统的串联谐振频率时,网络的输出信号中只含有逆变网络输出信号的基波,其余高次谐波分量可以忽略不计。也就是说,整流网络的输入信号为一个正弦量。所以可以认为该谐振变换器只通过基波传输能量,在工作过程中谐振电路中的各电量为正弦量。
输出电路是变换电路中压电变压器所有后端网络的总称,通常输出电路包含输出匹配网络、整流电路和负载电路。输出匹配网络的目的是使压电变压器的工作效率最大化,并减小流入压电变压器的无功功率。整流电路的作用是把交流能量转换为直流能量,高压小功率的应用场合中通常利用单相性的无源器件组成倍压整流电路。汽车安全气囊点火系统高压变换电路的负载电路主要包含高压发火电容和反馈回路中的分压电阻,与普通DCDC变换器的差别是,前者属电容充电电源,负载呈容性阻抗,高压电容一方面是变换器的负载,另一方面对输出脉动信号起滤波作用,减少对控制回路的干扰。负载电路中的电阻阻值较大,消耗的功率远小于变换电路的输出功率,作用是用来组成分压器对输出直流电压分压采样并反馈到控制电路中。而普通DC-DC变换器中负载电路中电容很小,主要起滤波作用,负载呈电阻性。
为了使整个变换电路在工作过程中效率最大化,下面分析输出电路工作在什么状态可以使电容充电效率达到最大。电容充电电源工作负载范围非常宽,可能近似于短路,也可能近似于开路,输出电压从零变到额定值。目前文献[83,84]给出的常用电容充电技术主要有如下三种:恒压电阻充电技术、谐振充电技术和高频变换器充电技术。上述三种技术各有特点,适用于不同的应用场合,其中恒压电阻充电技术主要应用于低功率输出,对电路的体积、调整性和效率要求不高的情况下,该技术的主要特点就是电路简单,但由于限流电路的存在,整个电路的充电效率最高为50%。谐振充电技术则适用于中高功率输出,充电回路含有用来存储能量的电感和电容以及二极管等器件,与恒压电阻充电技术相比,效率和输出调整性均有较大的提升。高频变换器充电技术适用于中高功率输出,且体积小,效率高,控制性能好,在电容充电电源中已得到广泛的应用。
为了获得最大效率的工作条件,这里利用电路分析的方法在理论上寻找充电电路工作的最佳过程。
1.连续电流的最佳充电过程分析
压电变压器输出级的电容典型充电网络如图3.5所示。C o为压电变压器的输出电容,C为负载高压电容,电阻R为整个回路的等效限流电阻,r为等效电容并联电阻,包括电压采样电阻、电容漏电阻等。
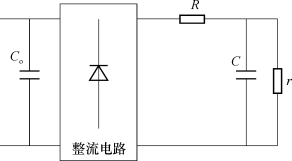
图3.5 压电变压器输出级电容充电网络
假设电容的初始电压为零,并设充电电流为i(t),电容两端电压为u C(t),电容容量为C。由于放电时间常数τ=rC远大于充电周期,放电过程的影响可以忽略。
回路中限流电阻消耗的能量可表示为
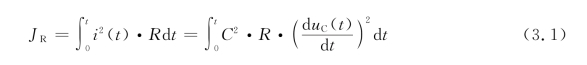
上式中的被积函数可以写成
![]()
为了求得J R的极小值,写出被积函数的欧拉-拉格朗日方程:

其中,
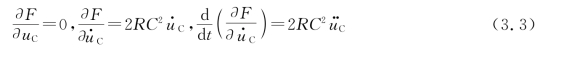
将式(3.3)代入式(3.2)得
![]()
因此电容上的电压可写成
![]()
式(3.5)中的A、B为常数。
对应的充电电流的表达式可表示为

代入初始和终值条件,u C=0,u C(t 0)=U C,得

应用工程数学的变分法,可以求得要使回路中电阻的消耗能量最少,充电电流应维持恒流充电特性。这样充电电压线性增长,效率最高。
对应的充电末期的充电效率为

显然,当回路的有效电阻为零时,充电效率将达到最大。当用恒流源向储能电容器充电时,尽可能减小充电回路的等效限流电阻,以获得较高的充电效率。
2.脉动电流的最佳充电过程分析
若充电电路的主电路为高频谐振功率变换电路,那么充电电流呈周期脉动特性,对应的变压器输出电压和负载电容的平均电压均呈阶梯状上升。
为了便于分析,用阶梯电压源来代替谐振变换器中压电变压器的平均输出电压。如图3.6所示,阶梯电压源共有n个阶梯,而第n个阶梯对应的电压值为U n。假设充电电路的等效限流电阻为R,负载电容容量为C。阶梯电压u作用于RC电路,且每个阶梯宽度远大于RC电路的时间常数。(https://www.daowen.com)
不失一般性,分析第k个阶梯作用于电路上时的充电规律,假设电容器C上的电压初始值为U k-1,在第k个区间有
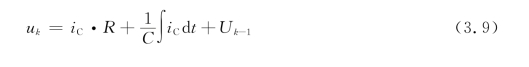
结合初始条件,可得在第k个区间充电电流:

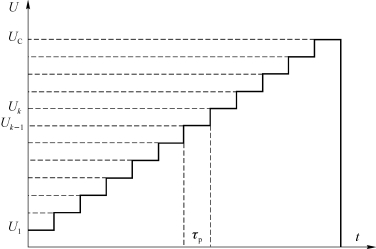
图3.6 等效阶梯电压源
所以该区间内任意时刻对应的电容两端电压为
![]()
在第k个阶梯电压作用期间,消耗在电阻R上的功率为
![]()
所以作用在τp的时间间隔内,电阻R上消耗的能量为
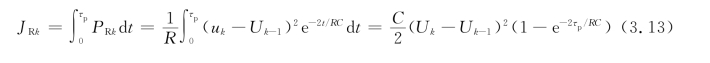
当τp≫RC时,

所以在n个阶梯中,消耗在电阻中的总能量为
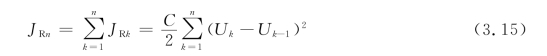
为了求得上式的最小值,令

则有
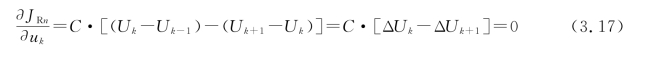
所以有
![]()
即等阶梯充电使回路电阻损耗最小。
电容的充电电压U C为

充电效率为

式中,
![]()
整理式(3.20),得

由上式可知,达到同样的充电电压U C,阶梯越多,其效率越高,也越近似于恒流充电。
