5.2.6 量子控制模式下驱动频率优选分析
开关频率是变换器设计的重要参数,这是因为首先压电变压器的工作效率、电压增益都是频率函数,所以频率的选择直接影响变压器的工作性能表现。其次,频率的选择还涉及变换器开关器件的软开关实现条件,且关系到整个变换器是否能实现对负载高压电容的恒流等台阶充电。实际应用中,发现若开关频率选择不当,轻则系统不能实现恒流充电,零电压开关,重则系统的输出电压不能达到预设要求。目前,由于国内外对压电变压器应用于电容充电电源领域的相关文献很少,至今未获得相关文献对量子模式控制下频率选择所做的详细分析。
量子控制模式结构简单,便于提高系统的可靠性,能满足本书研究背景的要求,但由于该模式下采用固定频率控制,因此在上述约束条件下,不能同时满足最优。本书主要通过上文分析过的恒流充电条件、零电压开关的实现条件以及实现最大电压增益等条件,来优化选择量子控制模式下的驱动频率值。
1.最大电压增益条件下的频率选择
对于给定负载,通常选择开关频率应使压电变压器工作处于获得最大增益状态。本书给出的拓扑电路中变压器负载为含有高压脉冲电容的倍压整流电路,在电容充电过程中变压器的等效负载随着充电电压值的变化而变化,充电过程中其最佳开关频率不是一个定值,而是一个频率区间。因此需从中选择一个较为优化的开关频率值。
当变换器的等效电路处于谐振时,压电变压器电压增益最大。随着工作周期的不断增加、输出电容电压的不断上升,为了获得理想的输出性能,选定的逆变电路开关频率应使整个变换电路在充电末期获得最大的电压增益。这里可以利用第3章的分析结论作为确定的理论依据。在应用中要注意,第3章的分析结果是建立在将变换器中容性阻抗为主等效成电阻阻抗为主的模型之上,工作频率特性刚好相反,因此在理解第3章的结论时需要做一下等效调整。图3.14所示的工作周期增大频率递减的特性代表实际变换器电路的工作频率呈递增特性。充电末期的工作频率可由曲线的第一个周期对应的频率来确定。
因此令m=1,将式(4.51)、式(4.53)代入式(4.41)可得变换器的工作频率为
79.4 k Hz,实际应用中,驱动频率f d的选择只要稍大于
即可为电路整个工作过程创造良好的实现软开关的条件,同时也能保证系统充电末期的升压性能。
2.等台阶充电条件下的频率选择
以变换器中压电变压器的主边之前电路为研究对象,当变换器对负载电容充电时,等效电路如图5.13所示,电路中的主要波形及关系如图5.14所示。在固定频率控制模式下,重点考虑在充电后期电路的等台阶充电条件。
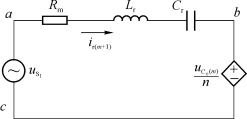
图5.13 压电变压器主边等效电路
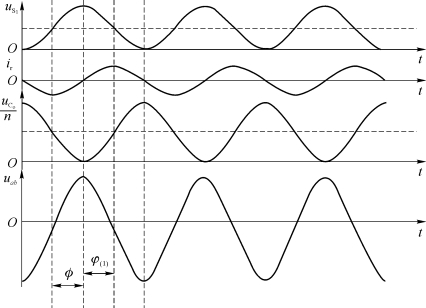
由4.3.1节的分析结果知,在充电后期输出电容电压的基波比谐振电流的相位滞后约四分之一周期,即|φ(1)|=90°,如图4.9所示。由于在选定频率时a、b两端间的阻抗一定,结合式(5.23)给出的等台阶充电条件,所以只要a、b间的电压u ab呈等台阶最大递增,即可近似满足系统的恒流充电要求,且能保证在给定输入电压下输出功率的最大化。对图5.14所示u S1、i r和u Co/n信号相位进行分析知,只要满足谐振电流i r与压电变压器的输入电压u S1之间的相位差φ约为90°,即可满足上述分析的条件。
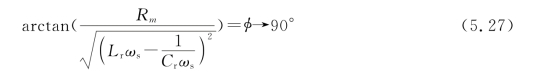
对应的驱动频率为
图5.14 谐振支路主要波形示意图
此时,u S1与u Co(1)/n刚好反向,所以a、b间的电压峰-峰值可以得到最大,且由于u Co(1)/n的最大值呈等台阶递增趋势,因此u ab的峰-峰值也呈等台阶递增。
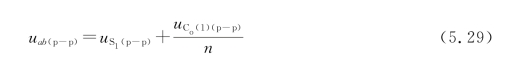
对应的谐振电流的峰-峰值为
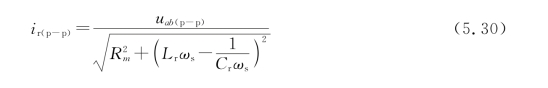
3.变换器工作过程等效模型频率确定
分析已经得知,在实现等台阶充电的条件下,导通角随着充电周期的增加不断减小。由5.2.3节的分析可知,对应的变换器工作过程中状态1和状态3持续时间逐渐增大,状态2和状态4持续时间逐渐缩短。在各个状态下,当等效电路处于谐振状态时,电路可以获得最大的谐振电流值,同时可以得到最大的电压增益。
状态2和状态4下的工作频率为
状态1和状态3下的工作频率为
分析可知,可以选择式(5.32)作为驱动频率的上限值,显然该值既可以满足在充电后期保证较大的升压比,同时因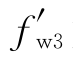
大于实际工作过程的工作频率,所以该频率值也能给软开关的实现创造良好的条件。
4.计算结果比较
将实验用变压器的参数值分别代入式(5.28)和式(5.32),这里选择采样分压电阻R L=100 MΩ,得到
。本节从不同的角度对开关驱动频率进行了分析计算,计算结果显示的基本一致性说明了当变换器的等效电路获得最大升压比时,也为恒流等台阶充电提供了实现条件,同时该计算结果也相互验证了各方法分析的正确性。由第3章的计算结果知,计算值要略大于实际测量值,因此在实际应用中,直接取计算值即已为零电压开关的实现创造了条件。