7.1.3 结合DDS技术的SPWM脉冲信号发生器的设计
结合DDS来产生SPWM信号的方案有文献进行过研究,但是这些方案普遍采用了比较复杂的框架,如图7.4所示。
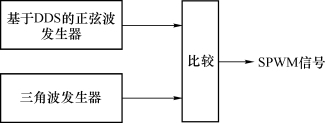
图7.4 SPWM发生器的框架图
图7.4中,DDS与三角波发生器分别产生完整的正弦信号与三角波信号,之后进行比较得到SPWM开关信号。在此种框架中,DDS与三角载波发生器为独立单元,增大了灵活性,但也增加了复杂性,降低了可靠性与运行速度。这里考虑到是为压电陶瓷变压器专门设计可调频的SPWM信号发生器,我们采用不同的、相对简洁的结构,如图7.5所示。
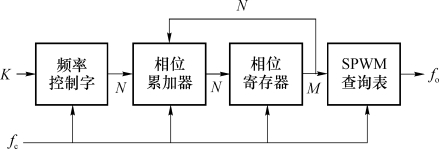
图7.5 SPWM发生器的组成结构
这里将DDS结构中的正弦查询表替换为SPWM信号查询表即可实现可调频率SPWM信号发生器。其中,SPWM查询表根据需要预先计算得出。下面我们开始介绍对这个信号发生器的设计。
为方便叙述,这里将原理重新阐述一下。前面的原理是一种框图结构,在实现上可以有很多种不同形式。由于我们将采用VHDL编码的形式,所以我们将所设计的SPWM发生器的原理用另一种样式表示,如图7.6所示。
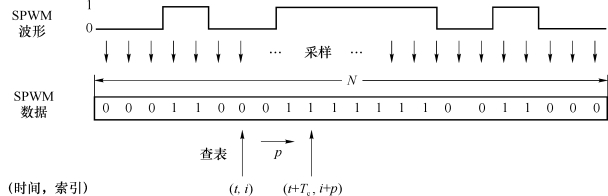
图7.6 SPWM信号发生器原理
本质上讲,这一SPWM发生器的核心是一个查表运算。考虑到SPWM波形的对称性,从SPWM波形的半个周期采样得到总数为N的SPWM数据构成查询表。于是产生SPWM信号只需要按照p的步进量及T c的时间间隔对其进行索引取值,步进量p越小,查找尺度越小,得到的波形就会在相应的尺度上越逼近采样源波形,精度也就越高,输出的SPWM信号频率f o=p·f c/N,其中,f c=1/T c。
信号发生器需要设置一些参数。在参数的取值上,我们需要满足一些条件。
第一,我们设计的驱动信号发生器需要尽量覆盖压电陶瓷变压器的工作频率。文献[130]中所使用的压电陶瓷变压器的最佳工作频率为74～80 k Hz,这里我们要求信号发生器的频率范围为0～200 k Hz。第二,驱动信号发生器需要具有一定的精度。参考Rosen型压电陶瓷变压器的频率特性,我们要求其具有1 k Hz的频率精度。所以,根据f o=p·f c/N,频率范围要求f o可以达到p·f c/N≥200 k Hz,精度上要求f c/N≤1 k Hz,同时为保证输出的SPWM信号波形失真小,应使得N≫p。
接下来,我们对SPWM信号发生器的查找表数据进行设计。查找表中的数据是对SPWM波形的采样,对查找表数据的设计关键就是选取一个合适的SPWM波形采样源。
如前所述,我们设计的可调频SPWM信号发生器需要针对两种场合:一种是用来驱动电路产生脉冲型电压;另一种是用来驱动电路产生正弦型电压。
首先针对第一种情况,我们可以设计这样的电路,在SPWM脉冲信号的控制下,电路可以输出脉冲型电压,如图7.7所示。
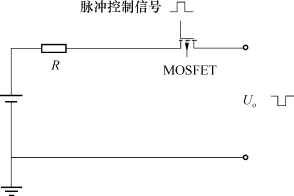
图7.7 脉冲型电压驱动电路
针对第二种情况,可以设计这样的电路,如图7.8所示。
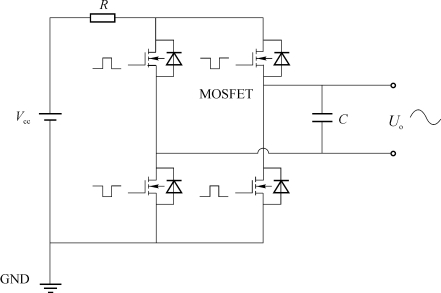
图7.8 正弦型电压驱动电路
当电路参数满足一些条件时,电路便可输出正弦型电压波形。电路的每个双桥控制周期由正负两个部分组成,考虑其正半周期,将电路简化,如图7.9所示。
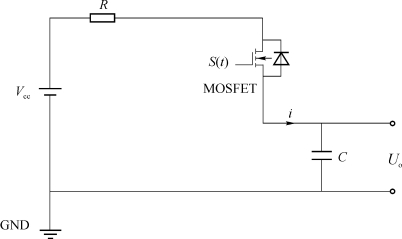
图7.9 正半周期等效电路
图7.9中,S(t)为开关控制信号,S(t)∈{0,1}。取此正半周期开始时刻t=0,正半周期区间[0,T p],并设初始时刻电容两端电压U o(0)=0 V。由电路基本理论得
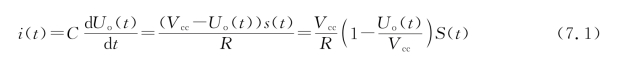
定性分析,当|U o(t)|≪V cc时,可以将i(t)视为仅由S(t)决定。为更好地设计参数,这里进行论述。
由式(7.1)可得
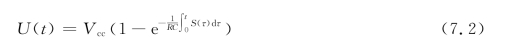
取α∈(0,1),我们要求
由式(7.2)可将式(7.3)化为
即
考虑到t∈[0,T p],S(t)∈{0,1},有t≤T p,S(t)≤1,于是,式(7.4)可以化为
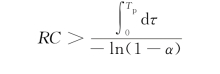
即
这样我们就求得了|U o(t)|≪V cc的等效约束条件。
而当|U o(t)|≪V cc,即当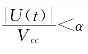
且α～o(1)时,由式(7.2)可得
即
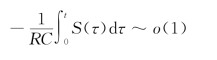
根据泰勒公式,得到
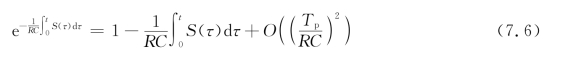
式(7.2)可以化为
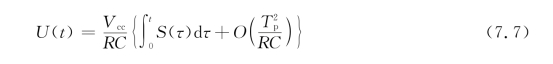
由于α～o(1),结合式(7.5)可以得到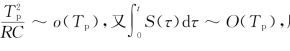
所以
这样,我们得到
接下来,我们就要对S(t)进行设计,使得U(t)成为正弦波形。一方面,由于这里S(t)由单极性三角波调制法产生,其关键的两个参数为调制系数m与三角波密度n,所以就需要对m和n进行选取。另一方面,我们要求U(t)成为正弦波,就需要一个评价标准,这里对U(t)进行频谱分析,将主频率成分在能量上的比重作为参考,进行SPWM波形的选取。即选取参数m、n,使得U(t)主频的能量比重最大。
一般而言,调制系数m的取值范围为(0,1],即0＜m≤1,而n为正整数。这里我们取m=1。对于参数n,由于单极性三角波调制法是采用周期性的“V”形三角波对正弦波进行采样,所以从趋势上分析,采样密度n越大,由采样得到SPWM信号可以产生的波形的主频能量比重越大,即越接近正弦波。
参数n的选取不仅要考虑S(t)积分信号对正弦波的逼近精度,同时要考虑S(t)自身的实现精度。由于S(t)开关信号由SPWM信号发生器产生,其精度就由信号发生器中查询表的精度决定,即受限于查询表对S(t)的采样密度。一方面,我们可以选取很大的n,构造出具有精细结构的S(t),从而其积分信号可以十分逼近标准正弦波,但是查询表的采样密度不够,不能将精细结构提取出来,我们也得不到如S(t)设计程度的U(t)信号。另一方面,我们设计的SPWM信号发生器是对查询表在等间隔的周期信号驱动下进行索引取值得到的,于是查询表对S(t)信号的采样也是等间隔的,这样采样位置的不同会造成采样结果的偏差,即参数n的不同导致采样密度变化,从而导致采样位置变化并造成采样结果的不同。所以,参数n的选取存在一个范围,而且并非越大越好,而是区间内的某个值。
综上分析,我们取三角载波的频率为100 k Hz,正弦波的频率为10 k Hz,调制系数m取为1,这样调制系数n=100/10=10,即正弦波一个周期内与三角载波的交点为10个,如图7.10和图7.11所示。
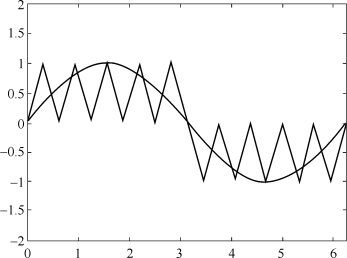
图7.10 m=1,n=10时SPWM信号的单极性三角波调制法
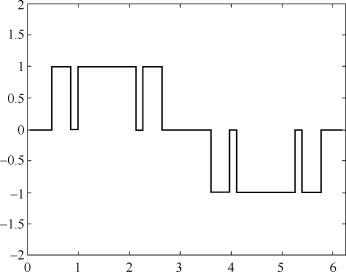
图7.11 m=1,n=10时的SPWM信号
为了建立查询表,我们需要对这个SPWM信号的一个完整周期进行采样,采样数目为N=100 000。由图7.11可以看出,1个周期的SPWM信号分为中点对称的前后两部分,可以由前半部分周期化后与相应倒相信号相乘得到。所以我们只需要对前半周期50 000个点建立查询表。而由于SPWM开关信号的值域为{0,1},所以我们只需要计算出其中的边界点,即0到1的边界点与1到0的边界点。
对于m=1,n=10时我们得到的SPWM信号,采用数学计算软件可以计算出这些点可以取为
7 680,13 815,15 811,34 189,36 185,42 320
如此,便建立了SPWM发生器的查询表。接下来便可以采用VHDL进行代码实现。这里仅对代码进行简要的介绍。
首先声明标准库并定义了一个名叫spwm的实体,该实体含有控制信号a、时刻信号clk,以及输出信号q与s。这里采用的时钟信号的频率是100 MHz。接下来便是程序的主体部分,即实体结构。
ar chi tecture spwm of spwm is
程序设计了一个循环计数结构对查询表进行取样输出,由不同的步进值step可以得到不同频率的输出。程序中设置step=99可以得到频率为100 k Hz的输出。在步进取样的过程中,参照关键点对当前位置进行判断即可获得当前SPWM信号值。